Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная/очно-заочная

ВЫПОЛНЕНИЕПРАКТИЧЕСКИХ ЗАДАНИЙПО ДИСЦИПЛИНЕЛогистикаГруппа Ср20М571СтудентМОСКВА 2023Разработатьтекущийпланпоприбыли(PR)приследующихпоквартальныхпоказателяхпообъемуреализованных товаров (Q), цене продукции (Р) и выручке (TR)заотчетныйпериод,представленныхвтабл.1.1.Таблица1.1Поквартальное распределение достигнутых показателейвотчетном периоде

№ квартала	Показатели	Варианты заданий
		1	2	3	4	5	6
1	Q, ед. тов.	360	520	600	690	1080	1150
	TR, ден. ед.	5400	4992	6600	8280	9600	10200
	PR, ден. ед.	1240	1048	1518	2240	2592	2754
2	Q, ед. тов.	350	480	575	720	1040	1200
	TR, ден. ед.	5250	4608	6325	8640	9200	9775
	PR, ден. ед.	1100	1060	1518	2074	2208	2542
3	Q, ед. тов.	410	460	675	718	920	1350
	TR, ден. ед.	6150	4416	7425	8616	10400	11050
	PR, ден. ед.	1350	972	2005	1982	2704	2652
4	Q, ед. тов.	380	540	650	811	960	1300
	TR, ден. ед.	5700	5184	7150	9720	10800	11475
	PR, ден. ед.	1140	1244	1859	2430	2484	2640

---

Наоснованииданныхрассчитываются параметры экономико-математической моделизависимостисуммыприбылиотвыручкиисводятсявтабл.1.2.Таблица1.2Параметрыэкономико-математическоймоделизависимостиприбылиотвыручки

№ кв.	yi (ден. ед.)	xi (ден. ед.)	yixi(тыс. ден. ед.)	x 2i (тыс. ден. ед.)	yxi	yi–уxi	(yi–yxi)2			y		 %
1	1240	5400	6696,0	29160,0	1162,5	77,5	6006,25		84,07		1207,50	6,96
2	1100	5250	5775,0	27562,5	1132,5	–32,5	1056,25
3	1350	6150	8302,5	37822,5	1230,0	120,0	14400,0
4	1140	5700	6498,0	42224,0	1222,5	–82,5	6806,25
ИТОГО	4830	22500	27271,5	136769,0	4747,5	82,5	28268,75

Допускается,чтозависимостьмеждуприбылью

---

ивыручкойноситлинейныйхарактер,т.е.у=а₀+а₁х_i.Тогда для составления системы нормальных уравненийn n nиспользуютсячисленныезначения(_y_i),(_x_i),(_y_ix_i),(уравненийприметвид:4830 = а₀4 +а₁22500,27271,5 =а₀22500 + а₁136769,0, (1.10)откудакоэффициента₀изпервогоуравнения_a4830a₁22500_{. (1.11)}0 ₄Подставляяегововтороеуравнение,найдему_xiпризначенияхвыручки _x_i=22500ден.ед.иприбылиi1n_y_i=4830ден.ед.приметвид:i1у_хi=82,5+0,2х_i. (1.12)Коэффициентрегрессииа₁ =0,2показываетвлияниенаприбыльосновного

---

определяющего фактора, выручки, т.е. на сколько рублей изменяется прибыль предприятия оптовой торговли при увеличении или снижении выручки, полученной им за год, на одну условную денежную единицу.

Коэффициент а₀ = 82,5 показывает влияние на прибыль всех остальных косвенных факторов, кроме выручки.

Подставляя в уравнение регрессии (1.12) значения х_i, получим значения расчетной прибыли (у_xi) по кварталам:

ух1 = 82,5 + 0,25400 = 1162,5 ден. ед.,
ух2 = 82,5 + 0,25250 = 1132,5 ден. ед.,	(1.13)
ух3 = 82,5 + 0,26150 = 1230,0 ден. ед.,
ух4 = 82,5 + 0,25700 = 1222,5 ден. ед.

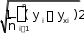
Среднееквадратическоеотклонение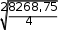  84,07.Арифметическое среднее от фактических значенийпоквартальнойприбыли(у)равноу¹n y^4830,01207,5ден.ед. (1.14)_i ni1 ⁴

---

показывает,чтоотклонениерасчетныхпоказателейотфактическихсоставляет6,96%.Например,припланируемойсуммевыручкинатекущийкварталвразмере8000ден.ед.прибыльсоставит у_х1=82,5+ 0,28000=1682,5ден.ед.Качествополученныхзначенийоцениваетсярасчетоминдексакорреляции,дляопределениякоторогонеобходиморассчитать величины остаточной ( σ²) и общей ( σ² ) дисперсий. Длянаглядностирасчетыиндексакорреляциисведенывтабл.1.3.Таблица1.3Расчетиндексакорреляции

№ квартал а	yi (ден.ед.)	у (ден.ед.)	yi–у	(yi–у)2	 2 ост	 2 общ	Ry,i
1	1240	1207,5	32,5	1056,25	7067,19	9368,75	0,5
2	1100		–107,5	11556,25
3	1350		142,5	20306,25
4	1140		–67,5	4556,25
ИТОГО	4830		0,0	37475,0

---

Смотрите также файлы

• Организация устного счета на уроках математики.doc

• Программа среднего профессионального образования 44. 02. 02 Преподавание в начальных классах Дисциплина Основы педагогического мастерства Практическое занятие 5.doc

• Студентке мінездеме алматы аласы, аза лтты ыздар Педагогикалык университетіні.docx

• Пояснительная записка программа учебноознакомительной практики предназначена для студентов 1 курса очной формы обучения оп в.pdf

• Лабораторная работа 1 21. 05. 04 Маркшейдерское дело знакомство с гис mapinfo ст гр 5гду Дежурный П. Д.doc