2.2 Расчёт среднегодовых расходов воды различной обеспеченности при недостаточности данных гидрометрических наблюдений.

По формуле (5) Qср_N = 5,35 м³/с

---

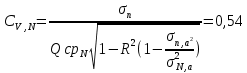(12)

При реализации второго метода ряд расчётной реки восстанавливается по уравнению линейной регрессии.

Таблица 13 – Приведение ряда среднегодовых расходов воды расчётной реки к длинному ряду реки-аналога.

№	Расход аналога	Расход расч	Qi(волна)	Qi
1	6,22		10,6	10,67
2	5,32		8,9	8,90
3	4,93		8,2	8,13
4	6,79		11,6	11,79
5	3,78		6,0	5,87
6	4,82		8,0	7,91
7	4,4		7,2	7,09
8	6,74		11,6	11,69
9	8		13,9	14,17
10	4,46		7,3	7,20
11	6,53	9,58		9,58
12	4,47	6,98		6,98
13	7,57	12,1		12,1
14	6,72	11,9		11,9
15	5,67	9,29		9,29
16	4,32	7,04		7,04
17	4,23	8,58		8,58
18	8,94	16,3		16,3
19	3,58	5,81		5,81
20	3,71	4,71		4,71
21	3,41	5,5		5,5
22	6,88	12		12
23	4,09	7,51		7,51
24	5,55	9,3		9,3
25	4,99	7,69		7,69
26	5,52	8,73		8,73
27	4,36	8,76		8,76

---

Продолжение таблицы 13

28	3,19	4,44		4,44
29	2,32	2,68		2,68
30	6,1	11,4		11,4
31	4,32	6,14		6,14
32	5,44	7,42		7,42
33	5,08	8,84		8,84
34	4,86	9,8		9,8
35	4,52	8,06		8,06
36	5,08	7,3		7,3
37	5,58	9,48		9,48
38	6,2	10,5		10,5
39	5,36	8,58		8,58
40	5,79	8,58		8,58
41	5,64	9,84		9,84
42	7,9	13,6		13,6
43	8,42	15,3		15,3
44	5,05	9,37		9,37
			среднее	9,01

---

Так же, как и при наличии длинного ряда наблюдений, в качестве расчетного значения Cs/Cv берем 1 и строим хронологический график среднегодовых расходов воды расчётной реки.



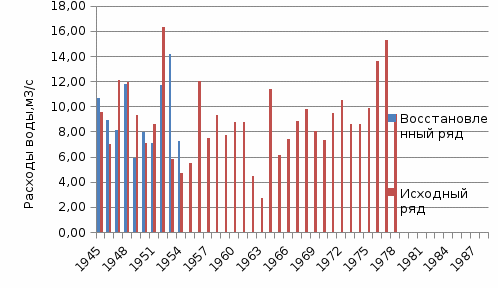
Рисунок 7 – Хронологический график среднегодовых расходов воды расчётной реки.

С использованием полученных статистических характеристик рассчитываем ординаты аналитической кривой обеспеченностей Крицкого-Менкеля.

Таблица 14 – Ординаты аналитической кривой обеспеченностей Крицкого-Менкеля для среднегодовых расходов воды расчётной реки.

P	0,1	1	5	10	25	50	75	90	95	99	99,9
kp	2,95	2,45	2	1,76	1,36	0,94	0,58	0,321	0,209	0,081	0,022
Qp	26,6	22,1	18,0	15,9	12,3	8,5	5,2	2,9	1,9	0,7	0,2

2.3 Расчёт среднегодовых расходов воды различной обеспеченности при отсутствии данных гидрометрических наблюдений

В данной работе принимается в качестве расчётных параметров норму стока и коэффициент вариации по реке-аналогу.

Так же как и в предыдущих пунктах в качестве расчётного значения Cs/Cv принимается за 1.

С использованием полученных статистических характеристик рассчитываются ординаты аналитической кривой обеспеченности Крицкого-Менкеля.

Таблица 15 – Ординаты аналитической кривой обеспеченности Крицкого-Менкеля для среднегодовых расходов воды расчётной реки.

---

P	0,1	1	5	10	25	50	75	90	95	99	99,9
kp	1,92	1,68	1,47	1,36	1,18	0,99	0,81	0,661	0,578	0,438	0,308
Qp	10,3	9,0	7,9	7,3	6,4	5,3	4,4	3,6	3,1	2,4	1,7

---

Смотрите также файлы

• Министерство образования и науки российской федерации федеральное государственное автономное образовательное учреждение высшего образования ЮжноУральский государственный университет.pdf

• Решение Сумма углов треугольника равна 180, поэтому третий угол равен 180 (48 79) 180 127 53.docx

• 2. Пути решения глобальных экологических проблем.docx

• азастан Республикасы ылым жне Жоары білім министрлігі М.темісов атындаы Батыс азастан университеті Физикаматематика факультеті Физика кафедрасы.docx

• Екі ос байланысы бар, жалпы.docx