Файл: Урок по теме Параллельность прямых и плоскостей. Бушева Инга Николаевна учитель математики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, параллельны).
- Сформулируйте свойство параллельных прямых в пространстве. (Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну)
- Какие прямые в пространстве называются скрещивающимися? (Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости и не пересекаются)
Задание 1 Вставьте пропущенные слова (индивидуальные карточки)
1) Единственную плоскость можно задать через три точки, при этом они … на одной прямой. (не лежат)
2) Если … точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости. (две)
3) Две различные плоскости могут иметь только одну общую … (прямую)
4) Прямые являются … в пространстве, если они не пересекаются и … в одной плоскости. (параллельными,лежат)
5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке В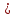
а, то прямые а и b …(скрещивающиеся)
Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем.
Критерии:
Всё правильно – 3 балла,
1 ошибка– 2 балла,
2 ошибки– 1 балл,
более 2 ошибок – 0 баллов.
Задание 2 Определите: верно, ли утверждение?
Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем.
Критерии:
всё правильно – 3 балла,
1, 2 ошибки– 2 балла,
3,4 ошибки– 1 балл,
более 4 ошибок – 0 баллов.
Задание 3Тест.
1.Прямые а и b скрещиваются с прямой с. Что можно сказать о прямых а и b?
а) взаимное расположение точно определить нельзя; +
б) скрещиваются или параллельны;
в) параллельны или пересекаются;
г) совпадают;
д) пересекаются или скрещиваются.
2. Выберите верное утверждение.
а) Две прямые называются параллельными, если они не имеют общих точек;
б) две прямые, параллельные третьей прямой, параллельны; +
в) две прямые, перпендикулярные третьей прямой, параллельны;
3. Прямая а, параллельная прямой b, пересекает плоскость α. Прямая с параллельна прямой b, тогда:
а) прямые а и с пересекаются;
б) прямая с лежит в плоскости α;
в) прямые а и с скрещиваются;
г) прямая b лежит в плоскости α;
д) прямые а и с параллельны. +
4. Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b?
а) скрещиваются или пересекаются;
б) пересекаются или параллельны;
в) скрещиваются или параллельны; +
г) только скрещиваются;
д) только параллельны.
5. Если две прямые не скрещиваются, то они
а) лежат в одной плоскости; +
б) только пересекаются;
в) совпадают;
г) только параллельны.
Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение.
Критерии:
всё правильно – 3 балла,
1 ошибка– 2 балла,
2 ошибки– 1 балл,
более 2 ошибок – 0 баллов.
З
Дано: ВС=АС,
СС1 АА1,
АА1=22 см
Найти: СС1
Решение:
АА1СС1, АС = ВС С1– середина А1В (по т.Фалеса)
С С1- средняя линия ∆АА1В
С С1= АА1 = 11 см
Ответ: 11см.
адание 4 Задача (3 балла)
Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем.
Блок – 3. Взаимное расположение в пространстве прямой и плоскости.
Цель блока:
- повторить и обобщить знания по теме взаимное расположение в пространстве прямой и плоскости;
- систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.
Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект.
- Взаимное расположение в пространстве прямой и плоскости.
а
а
α
α
а α а α а α
- Какие прямая и плоскость называются параллельными? (Прямая и плоскость называются параллельными, если они не пересекаются)
- Сформулируйте признак параллельности прямой и плоскости в пространстве. (Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.)
Задание 1 Тест. Учащиеся получают задание и выполняют его самостоятельно.
1. Прямые а и b параллельны одной плоскости . Как расположены прямые а и b относительно друг друга?
а) параллельны +
б) пересекаются +
в) скрещиваются +
2. Прямые а и b параллельны. Через каждую из них проведено по плоскости, которые пересекаются по прямой с. Как расположена прямая с по отношению к прямым а и b?
а) параллельно +
б) пересекает
в) перпендикулярно
3. Прямая а лежит в плоскости. Как расположена относительно плоскости прямая b, если b параллельна а?
а) перпендикулярно
б) параллельно +
в) пересекает
4. Сколько плоскостей можно провести через две данные точки?
а) одну
б) две
в) много +
5. Если одна из двух параллельных прямых пересекает плоскость, то другая прямая
а) параллельна плоскости
б) пересекает плоскость +
в) перпендикулярна плоскости
7. Точка А принадлежит плоскости α, точка В не принадлежит плоскости α. Принадлежит ли плоскости середина отрезка АВ.
а) да
б) нет +
в) не всегда
8. Прямая а параллельна прямой в, а прямая в параллельна плоскости . Взаимное расположение прямой а и плоскости .
а) параллельны +
б) пересекаются
в) скрещиваются
г) совпадают +
Учащиеся выполняют тест. Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем.
Критерии:
Всё правильно – 3 балла,
1, 2 ошибки– 2 балла,
3, 4 ошибки– 1 балл,
более 3 ошибок – 0 баллов.
A
В
С
З
В
адание 2 (3 балла) Плоскость проходит через сторону АС АВС. Точки D и E - середины отрезков АВ и BC соответственно. Докажите, что DE α.
Доказательство:
1. Точки D и E - середины отрезков АВ и BC соответственно
2. DE – средняя линия (по определению) DE АС (по свойству) DE α ( по признаку параллельности прямой и плоскости)
D
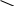
Е
А
С
α
Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение во время обсуждения этих вопросов вместе с учителем.
Задание 4(3 баллов) - дополнительное
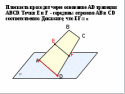
Доказательство:
Точки Е и F - середины отрезков АВ и СD
EF – средняя линия трапеции
EF АD EF α (по признаку параллельности прямой и плоскости).
Блок – 4. Взаимное расположение в пространстве двух плоскостей.
Цель блока:
- повторить и обобщить знания по теме взаимное расположение в пространстве двух плоскостей;
- систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.
Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект.
- Взаимное расположение в пространстве двух плоскостей.
α
β
α
β
β
α β
α и β - совпадают α β
- Какие плоскости называются параллельными? (Две плоскости называются параллельными, если они не пересекаются)
- На практике в столовой, где встречаетесь с параллельными плоскостями? (Нарезка хлеба, при нарезке хлеба плоскость ножа остается в параллельных плоскостях. Газовая плита и кастрюли стоящие на ней. Плоскость газовой плиты должна быть параллельна плоскости пола (т.к. горизонтальной). Если это не будет выполнятся, жидкость из кастрюли будет выливаться.)
- Сформулируйте признак параллельности плоскостей в пространстве. (Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости, то эти плоскости параллельны.)
- Сформулируйте свойства параллельных плоскостей.
1. Если плоскость пересекает две параллельные плоскости, то прямые пересечения параллельны.
2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Задание 1 Тест. Учащиеся получают задание и выполняют его самостоятельно.
1. Плоскость α параллельна прямой в, а прямая в параллельна плоскости . Взаимное расположение плоскостей α и .
а) параллельны +
б) пересекаются +
в) совпадают +
2. Плоскость пересекает плоскости α и β по параллельным прямым а и в. Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются +
в) совпадают
3. Каждая из плоскостей α и β параллельна плоскости . Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются
в) совпадают
4. Каждая из плоскостей α и β параллельна прямой а. Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются +
в) совпадают +
Учащиеся выполняют тест. Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди устно объясняют свое решение.
- Сформулируйте свойство параллельных прямых в пространстве. (Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну)
- Какие прямые в пространстве называются скрещивающимися? (Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости и не пересекаются)
Задание 1 Вставьте пропущенные слова (индивидуальные карточки)
1) Единственную плоскость можно задать через три точки, при этом они … на одной прямой. (не лежат)
2) Если … точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости. (две)
3) Две различные плоскости могут иметь только одну общую … (прямую)
4) Прямые являются … в пространстве, если они не пересекаются и … в одной плоскости. (параллельными,лежат)
5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке В
а, то прямые а и b …(скрещивающиеся)Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем.
Критерии:
Всё правильно – 3 балла,
1 ошибка– 2 балла,
2 ошибки– 1 балл,
более 2 ошибок – 0 баллов.
Задание 2 Определите: верно, ли утверждение?
| 1. Если прямая проходит через вершину треугольника, то она лежит в плоскости треугольника. | Нет |
| 2. Если прямые не пересекаются, то они параллельны. | Нет |
| 3. Прямая m параллельна прямой n, прямая m параллельна плоскости α. Прямая n параллельна плоскости α. | Да |
| 4. Все прямые пересекающие стороны треугольника лежат в одной плоскости. | Да |
| 5. Прямая АВ и точки С, D не лежат в одной плоскости. Могут ли прямые АВ и СD пересекаться? | Нет |
| 6. Прямые АВ и СD пересекаются. Могут ли прямые АС и ВD быть скрещивающимися? | Нет |
| 7. Прямые а и в не лежат в одной плоскости. Можно ли провести прямую с, параллельную прямым а и в? | Нет |
| 8. Прямая а, параллельная прямой в, пересекает плоскость α. Прямая с параллельна прямой в. Может ли прямая с лежать в плоскости α? | Нет |
| 9. Прямая а параллельна плоскости α. Существует ли на плоскости α прямые, непараллельные а? | Да |
Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем.
Критерии:
всё правильно – 3 балла,
1, 2 ошибки– 2 балла,
3,4 ошибки– 1 балл,
более 4 ошибок – 0 баллов.
Задание 3Тест.
1.Прямые а и b скрещиваются с прямой с. Что можно сказать о прямых а и b?
а) взаимное расположение точно определить нельзя; +
б) скрещиваются или параллельны;
в) параллельны или пересекаются;
г) совпадают;
д) пересекаются или скрещиваются.
2. Выберите верное утверждение.
а) Две прямые называются параллельными, если они не имеют общих точек;
б) две прямые, параллельные третьей прямой, параллельны; +
в) две прямые, перпендикулярные третьей прямой, параллельны;
3. Прямая а, параллельная прямой b, пересекает плоскость α. Прямая с параллельна прямой b, тогда:
а) прямые а и с пересекаются;
б) прямая с лежит в плоскости α;
в) прямые а и с скрещиваются;
г) прямая b лежит в плоскости α;
д) прямые а и с параллельны. +
4. Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b?
а) скрещиваются или пересекаются;
б) пересекаются или параллельны;
в) скрещиваются или параллельны; +
г) только скрещиваются;
д) только параллельны.
5. Если две прямые не скрещиваются, то они
а) лежат в одной плоскости; +
б) только пересекаются;
в) совпадают;
г) только параллельны.
Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение.
Критерии:
всё правильно – 3 балла,
1 ошибка– 2 балла,
2 ошибки– 1 балл,
более 2 ошибок – 0 баллов.
З
Дано: ВС=АС,
СС1 АА1,
АА1=22 см
Найти: СС1
Решение:
АА1СС1, АС = ВС С1– середина А1В (по т.Фалеса)
С С1- средняя линия ∆АА1В
С С1= АА1 = 11 см
Ответ: 11см.
адание 4 Задача (3 балла)
Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем.
Блок – 3. Взаимное расположение в пространстве прямой и плоскости.
Цель блока:
- повторить и обобщить знания по теме взаимное расположение в пространстве прямой и плоскости;
- систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.
Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект.
- Взаимное расположение в пространстве прямой и плоскости.
а
а
α
α
а α а α а α- Какие прямая и плоскость называются параллельными? (Прямая и плоскость называются параллельными, если они не пересекаются)
- Сформулируйте признак параллельности прямой и плоскости в пространстве. (Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.)
Задание 1 Тест. Учащиеся получают задание и выполняют его самостоятельно.
1. Прямые а и b параллельны одной плоскости . Как расположены прямые а и b относительно друг друга?
а) параллельны +
б) пересекаются +
в) скрещиваются +
2. Прямые а и b параллельны. Через каждую из них проведено по плоскости, которые пересекаются по прямой с. Как расположена прямая с по отношению к прямым а и b?
а) параллельно +
б) пересекает
в) перпендикулярно
3. Прямая а лежит в плоскости. Как расположена относительно плоскости прямая b, если b параллельна а?
а) перпендикулярно
б) параллельно +
в) пересекает
4. Сколько плоскостей можно провести через две данные точки?
а) одну
б) две
в) много +
5. Если одна из двух параллельных прямых пересекает плоскость, то другая прямая
а) параллельна плоскости
б) пересекает плоскость +
в) перпендикулярна плоскости
7. Точка А принадлежит плоскости α, точка В не принадлежит плоскости α. Принадлежит ли плоскости середина отрезка АВ.
а) да
б) нет +
в) не всегда
8. Прямая а параллельна прямой в, а прямая в параллельна плоскости . Взаимное расположение прямой а и плоскости .
а) параллельны +
б) пересекаются
в) скрещиваются
г) совпадают +
Учащиеся выполняют тест. Пары обмениваются решениями и проверяют работы друг друга во время обсуждения этих вопросов вместе с учителем.
Критерии:
Всё правильно – 3 балла,
1, 2 ошибки– 2 балла,
3, 4 ошибки– 1 балл,
более 3 ошибок – 0 баллов.
A
В
С
З
В
адание 2 (3 балла) Плоскость проходит через сторону АС АВС. Точки D и E - середины отрезков АВ и BC соответственно. Докажите, что DE α.
Доказательство:
1. Точки D и E - середины отрезков АВ и BC соответственно
2. DE – средняя линия (по определению) DE АС (по свойству) DE α ( по признаку параллельности прямой и плоскости)
D
Е
А
С
α
Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение во время обсуждения этих вопросов вместе с учителем.
Задание 4(3 баллов) - дополнительное
Доказательство:
Точки Е и F - середины отрезков АВ и СD
EF – средняя линия трапеции
EF АD EF α (по признаку параллельности прямой и плоскости).
Блок – 4. Взаимное расположение в пространстве двух плоскостей.
Цель блока:
- повторить и обобщить знания по теме взаимное расположение в пространстве двух плоскостей;
- систематизировать полученные знания.
Актуализация опорных знаний. Проведем теоретическую разминку.
Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект.
- Взаимное расположение в пространстве двух плоскостей.
α
β
α
β
β
α β
α и β - совпадают α β
- Какие плоскости называются параллельными? (Две плоскости называются параллельными, если они не пересекаются)
- На практике в столовой, где встречаетесь с параллельными плоскостями? (Нарезка хлеба, при нарезке хлеба плоскость ножа остается в параллельных плоскостях. Газовая плита и кастрюли стоящие на ней. Плоскость газовой плиты должна быть параллельна плоскости пола (т.к. горизонтальной). Если это не будет выполнятся, жидкость из кастрюли будет выливаться.)
- Сформулируйте признак параллельности плоскостей в пространстве. (Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости, то эти плоскости параллельны.)
- Сформулируйте свойства параллельных плоскостей.
1. Если плоскость пересекает две параллельные плоскости, то прямые пересечения параллельны.
2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Задание 1 Тест. Учащиеся получают задание и выполняют его самостоятельно.
1. Плоскость α параллельна прямой в, а прямая в параллельна плоскости . Взаимное расположение плоскостей α и .
а) параллельны +
б) пересекаются +
в) совпадают +
2. Плоскость пересекает плоскости α и β по параллельным прямым а и в. Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются +
в) совпадают
3. Каждая из плоскостей α и β параллельна плоскости . Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются
в) совпадают
4. Каждая из плоскостей α и β параллельна прямой а. Взаимное расположение плоскостей α и β.
а) параллельны +
б) пересекаются +
в) совпадают +
Учащиеся выполняют тест. Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди устно объясняют свое решение.