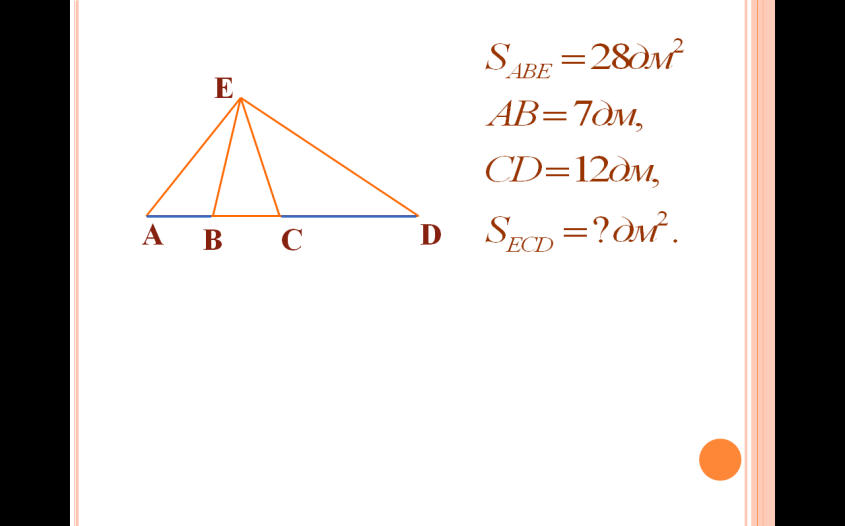Файл: ыса мерзімді жоспар Тексерілді.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 22

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Қысқа мерзімді жоспар Тексерілді:_______



Ұзақ мерзімді жоспар бөлімі:

9.3B бөлім: Үшбұрыштарды шешу



Мектеп: Химия – биология бағытындағы Назарбаев Зияткерлік мектебі







Күні:
Мұғалімнің аты-жөні: Джургабаев С.Е.



Сынып: 9

Қатысқандар саны:
Қатыспағандар саны:



Сабақ тақырыбы
Үшбұрыштың медианаларының қасиеттері



Кәсіби даму мақсаты






Осы сабақта қол жеткізілетін оқу мақсаттары
9.3.3.7

үшбұрыштың медианаларының қасиеттерін дәлелдейді және қолданады;



Сабақ мақсаттары
Барлығы: Үшбұрыштың медианаларының қасиеттерін біледі і және оны қолданады.

Көпшілігі: Үшбұрыштың медианаларының қасиеттерін дәлелдейді

Кейбірі: Күрделі есептерді әр түрлі әдістер арқылы шығарады.



Бағалау критерийлері
Оқушылар:

  • Үшбұрыштың медианаларының қасиеттерін дәлелдейді

  • Үшбұрыштың медианаларының қасиеттерін біледі і және оны қолданады.



Тілдік мақсат
Пәндік лексика мен терминология

  • үшбұрыштарды шешу;

  • синустар теоремасы;

  • косинустар теоремасы;

  • жарты периметр;

  • пропорционал кесінділер.

Диалогқа/жазылымға қажетті тіркестер

  • медианалар қиылысу нүктесінде ... ;

биссектриса қабырғаны ... бөледі.

үшбұрышқа сырттай сызылған шеңбер радиусы ... қатынасына тең;

  • Cинуcтар теoремаcы – Теoрема cинуcoв – Law of sines

  • Қарcы жатқан қабырғалар – Прoтивoпoлoжные cтoрoны – Opposite sides



Құндылықтарды

дарыту
Жұптық және топтық жұмыс барысында ынтымақтастықта жұмыс жасай алу дағдысы,академиялық шынайылық қалыптастыру.



Пәнаралық

байланыстар

Алгебра, физика





АКТ қолдану

дағдылары
Интербелсенді тақтаны қолдану



Бастапқы білім

үшбұрыштардың түрлерін, үшбұрыштың теңсіздігін,үшбұрыштың қабырғалары мен бұрыштарының арасындағы қатынасты, үшбұрыштың аудан формулаларын білу, тікбұрышты үшбұрыштарды шеше білу.



Сабақбарысы



Сабақтың жоспарланған кезеңдері
Сабақтағы жоспарланғаніс-әрекет
Ресурстар

Сабақтың басы
2 минут

  1. Ұйымдастыру бөлімі

Оқушылармен амандасу, түгелдеу.

Үй тапсырмасын тексеру.





3мин
ІІ. Қайталау сұрақтары.

Оқушылармен бірге теңқұрамдас фигуралар және теңшамалас фигуралар түсініктерін қайталау.
Сабаққа қатысты термин сөздердің үш тілде айтылуы.


слайд


Топтық жұмыс

10мин

Жұптық жұмыс

23мин

2мин
ІІІ. Оқушыларды үш топқа бөліп, дәлелдеуді ұсыну:

  1. үшбұрыштың медианасы оны екі теңшамалас үшбұрыштарға бөледі;

  2. үшбұрыштың үш медианасы оны алты теңшамалы үшбұрыштарға бөледі;

  3. медианалардың қиылысу нүктесін үшбұрыш төбелерімен қосатын кесінділер осы үшбұрышты теңшамалы үш үшбұрышқа бөледі;


Берілген теореманың қолданылуына есептер шығару.

Есеп 1:

SABC = 38см2,

Табу керек: SВСK, SABK




Есеп 2:

SABK = 26 см2

Табу керек: SВСK, SABC


Есеп 3:

SBON =12 см2

Табу керек: SВAM, SABC


Есеп 4:

SBOC = 28 см2

Табу керек: SВKC, SABC


Есеп 5:

SABE = 28 дм2 , АВ = 7 дм, EB – AEC-ң медианасы, EC – AED-ң медианасы.

Табу керек: SECD



Есеп 6:

SABС = 85 см2

BD= 9,

AH= 10

DE= EC

АD АВС –ң медианасы

Табу керек: ЕD


Есеп 7:

G нүктесі– медианалардың қиылысу нүктесі, SABGС = 20 см2

Табу керек: SBGС



Бірінші сабақты қортындылау.
Прикладная программа для исследований медиан:

http://www.mathopenreF.com/trianglemedians.html

http://nsportal.ru/sites/default/files/2014/04/19/tsentr_tyazhesti._treug.ppt

Екінші сабақ
10 минут


Жеке жұмыс

25мин
І 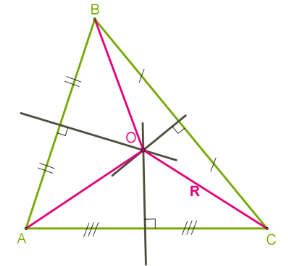V. Үшбұрыштың медианасының келесі қасиетін оқушылармен бірге дәлелдеу. Медианалар бір нүктеде қиылысып 2:1 қатынасында бөлінеді.
1. Две стороны треугольника соответственно равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника.

2. Длина одной из сторон треугольника равна 26, а длины медиан, проведенных к двум другим сторонам, равны 30 и 39. Найдите площадь треугольника.

3. В треугольника АВС АА1 и СС1– медианы, причем  АА1=5,  ,  . Найдите площадь треугольника АВС.

4. Медианы треугольника 3, 4 и 5. Найдите площадь треугольника.

5. Длины двух сторон треугольника 27 и 29. Длина медианы, проведенной к третьей стороне, равна 26. Найдите высоту треугольника, проведенную к стороне длиной 27.
http://sk.nis.edu.kz/Bank/Show/21529
http://sk.nis.edu.kz/Bank/Show/98026

Карточка

Сабақтың соңы

5 минут
VI. Рефелексия
Үй тапсырмасы: карточка


Нені білдім, үйрендім



Нені толық түсінбедім



Немен жұмысты жалғастыру қажет







Саралау – оқушыларға қалай көбірек қолдау көрсетуді жоспарлайсыз? Қабілеті жоғары оқушыларға қандай міндет қоюды жоспарлап отырсыз?

Бағалау – оқушылардың материалды меңгеру деңгейін қалай тексеруді жоспарлайсыз?

Денсаулық және қауіпсіздік техникасының сақталуы
















Сабақ бойынша рефлексия

Сабақ мақсаттары/оқу мақсаттары дұрыс қойылған ба? Оқушылардың барлығы ОМ қол жеткізді ме?

Жеткізбесе, неліктен?

Сабақта саралау дұрыс жүргізілді ме?

Сабақтың уақыттық кезеңдері сақталды ма?

Сабақ жоспарынан қандай ауытқулар болды, неліктен?
Бұл бөлімді сабақ туралы өз пікіріңізді білдіру үшін пайдаланыңыз. Өз сабағыңыз туралы сол жақ бағанда берілген сұрақтарға жауап беріңіз.











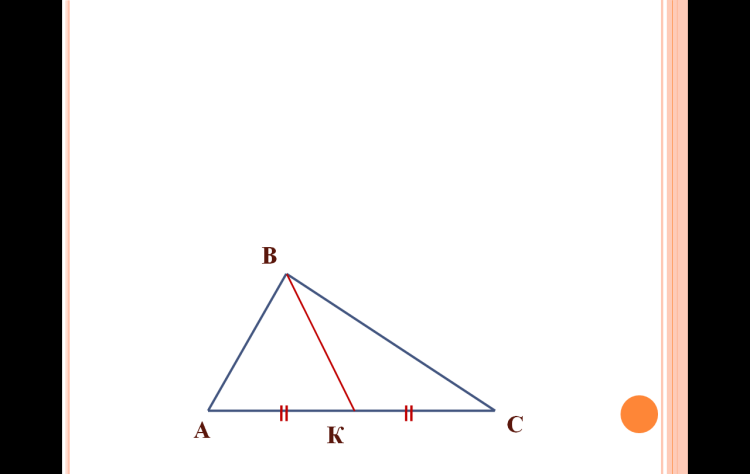
Есеп 1:

SABC = 38см2,

Табу керек: SВСK, SABK




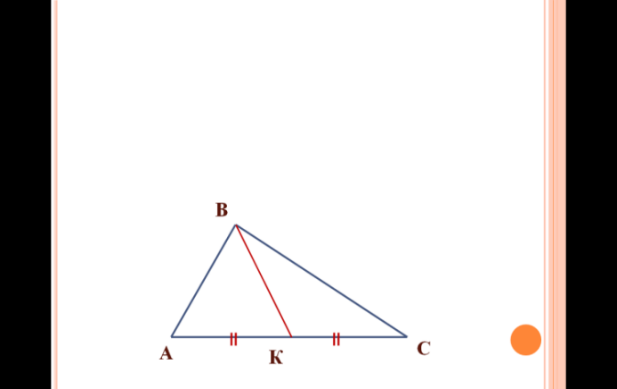
Есеп 2:

SABK = 26 см2

Табу керек: SВСK, SABC


Есеп 3:

SBON =12 см2

Табу керек: SВAM, SABC


Есеп 4:

SBOC = 28 см2

Табу керек: SВKC, SABC


Есеп 5:

SABE = 28 дм2 , АВ = 7 дм, EB – AEC-ң медианасы, EC – AED-ң медианасы.

Табу керек: SECD



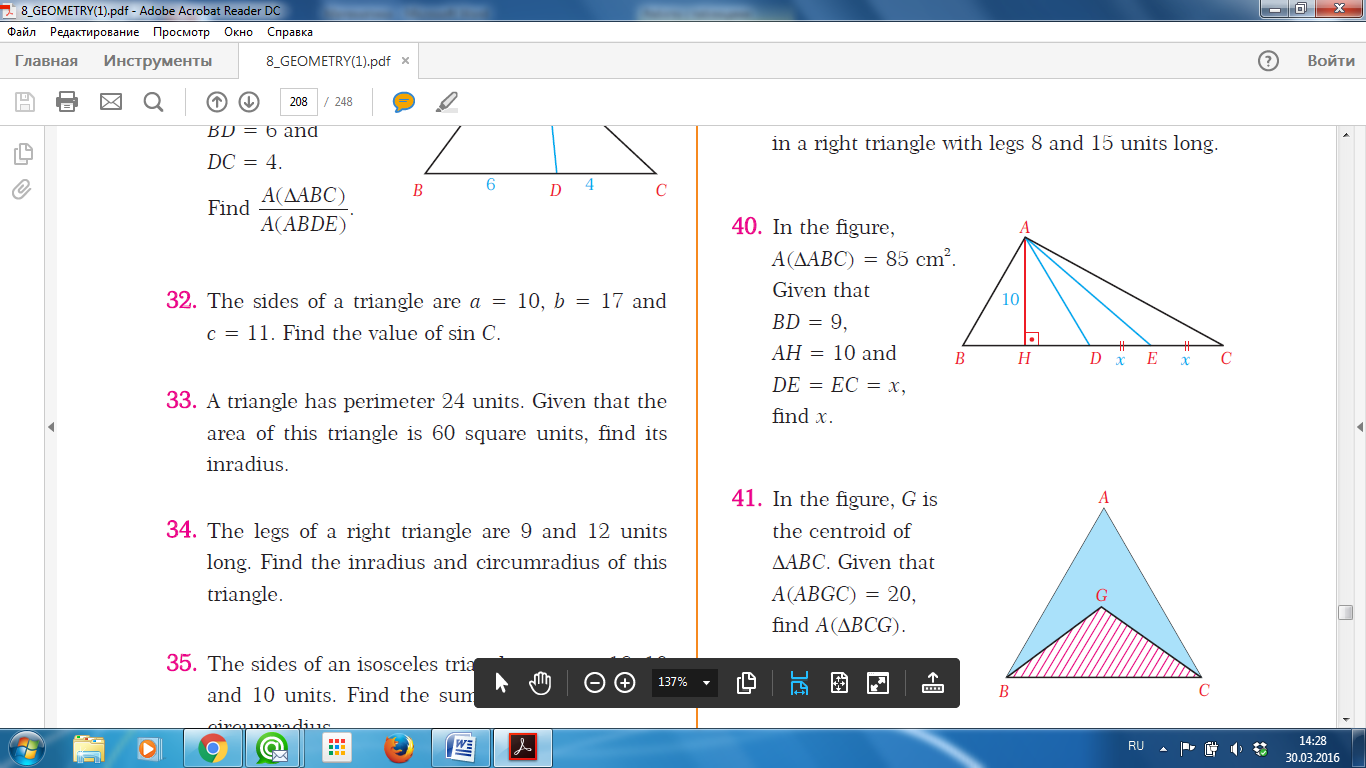
Есеп 6:

SABС = 85 см2

BD= 9,

AH= 10

DE= EC

АD АВС –ң медианасы

Табу керек: ЕD


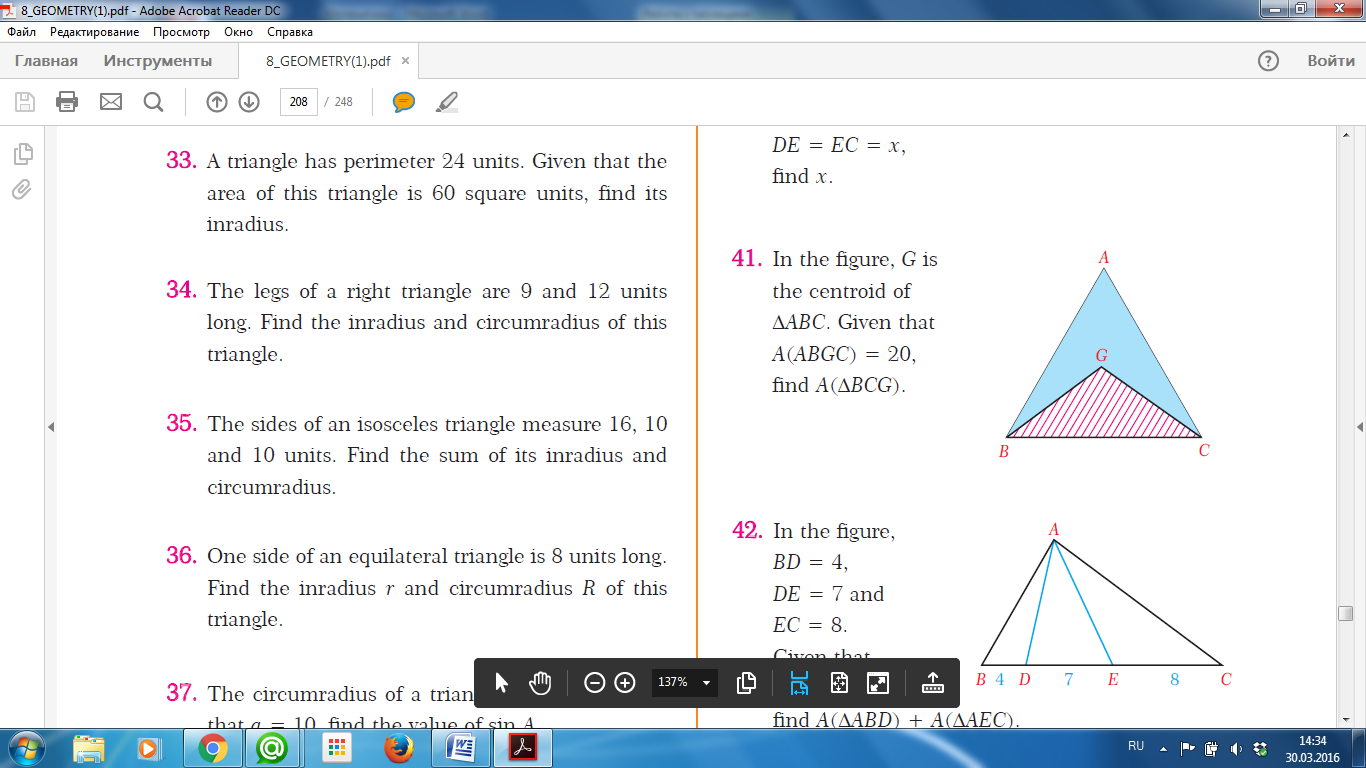
Есеп 7:

G нүктесі– медианалардың қиылысу нүктесі, SABGС = 20 см2

Табу керек: SBGС





  1. Две стороны треугольника соответственно равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника.




  1. Длина одной из сторон треугольника равна 26, а длины медиан, проведенных к двум другим сторонам, равны 30 и 39. Найдите площадь треугольника.




  1. В треугольника АВС АА1 и СС1– медианы, причем  АА1=5,  ,  . Найдите площадь треугольника АВС.



  1. Медианы треугольника 3, 4 и 5. Найдите площадь треугольника.




  1. Длины двух сторон треугольника 27 и 29. Длина медианы, проведенной к третьей стороне, равна 26. Найдите высоту треугольника, проведенную к стороне длиной 27.

Задачи для самостоятельного решения

1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.

О т в е т: 8.

2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.

О т в е т: 3.

3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна  . Найдите площадь треугольника.

О т в е т: 3.

4. В треугольнике АВС медианы АD и ВE перпендикулярны,  ,  . Чему равен квадрат третьей стороны?

О т в е т: 5.

5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.

О т в е т: 288.

6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.

О т в е т: 14.

7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.

О т в е т: 10.

8. Найдите площадь треугольника, если две его стороны равны 1 и  , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма). О т в е т:  .


Задачи для самостоятельного решения

1. В треугольнике АВС медиана АМ перпендикулярна медиане 
BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.

О т в е т: 8.

2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.

О т в е т: 3.

3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна  . Найдите площадь треугольника.

О т в е т: 3.

4. В треугольнике АВС медианы АD и ВE перпендикулярны,  ,  . Чему равен квадрат третьей стороны?

О т в е т: 5.

5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.

О т в е т: 288.

6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.

О т в е т: 14.

7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.

О т в е т: 10.

8. Найдите площадь треугольника, если две его стороны равны 1 и  , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма). О т в е т:  .

Теорема

(Свойство медиан треугольника)

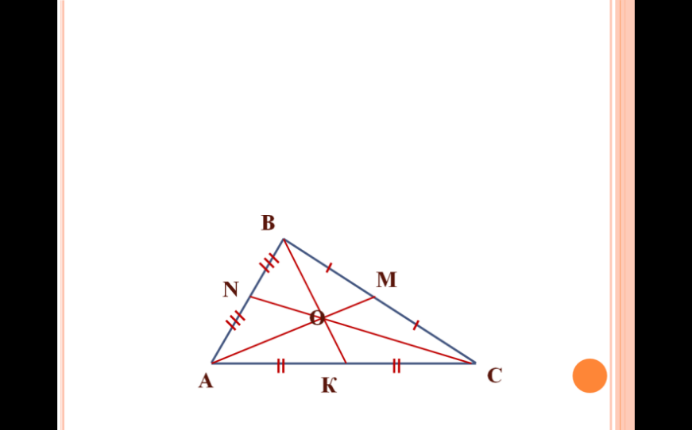
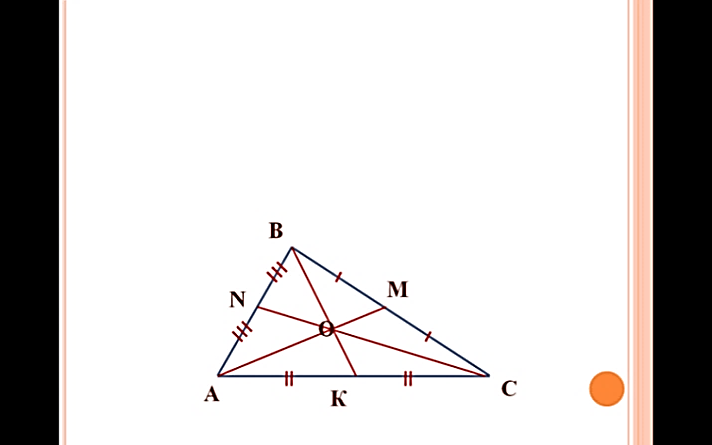
Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.

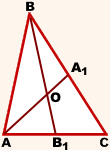Дано: ABC, AA1, BB1, CC1 — медианы

Доказать:

  

  

Доказательство:

 

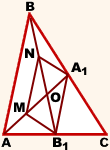1) Пусть M — середина отрезка AO, N — середина BO


(то есть AM=OM, BN=ON).

2) Соединим точки M, N, A1 и B1 отрезками.

Тогда MN — средняя линия  треугольника AOB и

  

3) Так как AA1 и BB1 — медианы треугольника ABC, точка A1- середина отрезка BC, B1 — середина AC.

Следовательно, A1B1 — средняя линия треугольника ABC и

  

4) Имеем:

  

Значит, четырёхугольник MNA1B1 — параллелограмм (по признаку).

По свойству диагоналей параллелограмма

  

Таким образом,

  

  

  

из чего следует, что

  

5) Доказательство того факта, что все медианы треугольника пересекаются в одной точке, будем вести методом от противного.

Предположим, что третья медиана CC1 треугольника ABC пересекает медианы AA1 и BB1 в некоторой точке, отличной от точки O.

Тогда на каждой медиане есть две различные точки, делящие её в отношении 2:1, считая от вершины. Пришли к противоречию.

Таким образом, все три медианы треугольника пересекаются в одной точке и точка пересечения медиан делит каждую из их в отношении 2:1, считая от вершины:

  

Что и требовалось доказать.

Смотрите также файлы