ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 37
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практикалық сабақ № 16
Тақырып:Полиномдық схема.
n – тәуелсіз тәжрибелер саны, осы тәжрибенің әр қайсысында үйлесімсз N нәтижелер
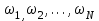 көрінеді. Ол нәтижелердің сәйкес ықтималдықтар
көрінеді. Ол нәтижелердің сәйкес ықтималдықтар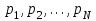 және ол ықтималдықтар тәжрибеден тәжрибеге өткенде өзгермейді,
және ол ықтималдықтар тәжрибеден тәжрибеге өткенде өзгермейді, 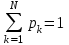 .
.А={
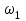 тәтижесі
тәтижесі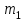 рет қайталанады,
рет қайталанады, 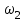 нәтижесі
нәтижесі 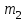 рет қайталанады,...,
рет қайталанады,..., 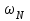 нәтижесі
нәтижесі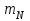 рет қайталанады }. Осы оқиғаның ықтималдығын табу керек.
рет қайталанады }. Осы оқиғаның ықтималдығын табу керек.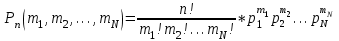 ,
, 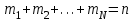 . Бернулли көпмүшелігін алдық.
. Бернулли көпмүшелігін алдық.Мысал. Қорапта 8 ақ, 5 қызыл, 2 қара шарлар бар. 5 шар біреуден, қайтарылу арқылы суырылады. Мына оқиғалардың ықтималдықтарын есептеңіз:
А={3 ақ шар, қалғандырынан біреуден алынады};
В={3 ақ шар алынады};
С={қатар 3 ақ шар, қалғандырынан біреуден алынады};
Шешімі.А оқиғасы үшін n=5, N=3. Р1=8/15 - әрбір ақ шардың көріну ықтималдығы;
Р2=5/15 - әрбір қызыл шардың көріну ықтималдығы;
Р3=2/15 - әрбір қара шардың көріну ықтималдығы;
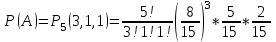 .
.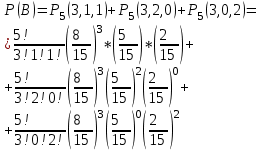
Әдебиеттер:
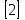 ,
, ,
, ,
,  , [10] §1, 14 тарау; [9], I тарау §1. [24], I тарау §1.
, [10] §1, 14 тарау; [9], I тарау §1. [24], I тарау §1.Бағалау критерийлері:
| 90-100 | Есептердің орындалуының кем дегенде 90% - ның болуы (жазбаша) |
| 70-89 | eceпті шығару тәсілін білгенмен оны орындау барысында қателіктер жібереді, яғни өздері жіберген қателерді іздеп табу жолдарын білмейді |
| 50-69 | Студент ішінара дұрыс жауаптар береді, иллюстрациялық мысалдар келтірмейді, зерттеліп отырған мәселе бойынша өз пікірін қалыптастыра алмайды, қателіктер жібереді немесе толық жауап бере алмайды. |
| 0-49 | Есептің шығарылмауы немесе тіпті қате ығарылуы. |
| Сабақ барысында студент сұрақтарға жауап бермейді немесе оның жауаптарында қателіктер бар. |
Практикалық сабақ № 17,18
Тақырып: Ықтималдық теориясының шектік теоремалары.
Мақсаты: Муавр-Лапластың локалдық, интегралдық теоремаларына есептер қарастыру.
Әдебиеттер:
 ,
, ,
, ,
,  , [10] §1, 14 тарау; [9], I тарау §1. [24], I тарау §1.
, [10] §1, 14 тарау; [9], I тарау §1. [24], I тарау §1.Бағалау критерийлері:
| 90-100 | Есептердің орындалуының кем дегенде 90% - ның болуы (жазбаша) |
| 70-89 | eceпті шығару тәсілін білгенмен оны орындау барысында қателіктер жібереді, яғни өздері жіберген қателерді іздеп табу жолдарын білмейді |
| 50-69 | Студент ішінара дұрыс жауаптар береді, иллюстрациялық мысалдар келтірмейді, зерттеліп отырған мәселе бойынша өз пікірін қалыптастыра алмайды, қателіктер жібереді немесе толық жауап бере алмайды. |
| 0-49 | Есептің шығарылмауы немесе тіпті қате ығарылуы. |
| Сабақ барысында студент сұрақтарға жауап бермейді немесе оның жауаптарында қателіктер бар. |
2 – модуль. Кездейсоқ шамалар
Практикалық сабақ № 19,20
Тақырып: Кездейсоқ шамалар. Дискретті кездейсоқ шаманың үлестірім заңдары
Мақсаты: Кездейсоқ шамалар ұғымын енгізу, мысалдар.
Негізгі сұрақтар, тапсырмалар:
1. Кездейсоқ шама. Мысал. Түрлері.
2. Дискретті кездейсоқ шаманың үлестірім заңы, көпмүшелігі.
3. Биномдық үлестірім заңы.
4. Пуассондық үлестірім.
5. Геометриялық үлестірім. Гипергеометриялық үлестірім заңы.
Тапсырмалар:
1. Х дискреттік кездейсоқ шаманың үлестірілім заңы берілді. Табу керек:
-
М(х) математикалық үмітін -
Д(х) дисперсиясын -
σ орташа квадраттық ауытқуын.
| х | 23 | 25 | 28 | 29 |
| У | 0,3 | 0,2 | 0,4 | 0,1 |
2. Х кездейсоқ шамасы F(х) интегралдық үлестірім
функциясы арқылы берілді. Табыңдар:
-
f(х) дифференциалдық үлестірім функциясын
(үлестірім тығыздығын)
-
М(х) математикалық үмітін -
Д(х) дисперсиясын
F(х)=
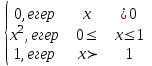
3. Х үзіліссіз кездейсоқ шаманың (0;π/2) интервалында үлестірім тығыздығы f(х)=Сsin3х, интервалдан тыс f(х)=0. С параметрін тап.
Негізгі сұрақтар, тапсырмалар:
Көп өлшемді кездейсоқ шамалар. Кездейсоқ шамалардың тәуелсіздігі, кездейсоқ шамалардың үлетірім заңдары.
Әдістемелік нұсқаулықтар:
1. Х дискреттік кездейсоқ шаманың үлестірілім заңы берілді. Табу керек:
-
М(х) математикалық үмітін -
Д(х) дисперсиясын -
σ орташа квадраттық ауытқуын
| Х | 17 | 21 | 25 | 27 |
| р | 0,2 | 0,4 | 0,3 | 0,1 |
2. Х кездейсоқ шамасы F(х) интегралдық үлестірім функциясы арқылы берілді.
Табыңдар:
-
f(х) дифференциалдық үлестірім тығыздығын -
М(х) математикалық үмітін -
Д(х) дисперсиясын
F(х)=
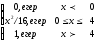
3. Х дискреттік кездейсоқ үлестірілім заңы бойынша берілген.
| Х | 2 | 6 | 10 |
| Р | 0,5 | 0,4 | 0,1 |
Осы шаманың үлестірім функциясының графигін салыңдар.
Мысал ретiнде қарапайым бiрқалыпты үлестiру функциясын қарастырайық.
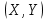 осьтерi бойынша бiрқалыпты үлестiрiлген х жəне у – екi кездейсоқ шамаларды алайық. Сонда
осьтерi бойынша бiрқалыпты үлестiрiлген х жəне у – екi кездейсоқ шамаларды алайық. Сондаdw(x) = C dx, dw( y) = C dy
Бұл екi кездейсоқ шаманың жазықтықта үлестiрiлуi де бiрқалыпты болады:
dw(x,y) = C
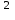 dxdy
dxdy Яғни ықтималдық (dxdy) аудан элементiне ғана тəуелдi .
Ал егер тiк бұрышты декарт координаталар жүйесiнен полярлық координатаға ауыссақ (r,
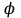 ),
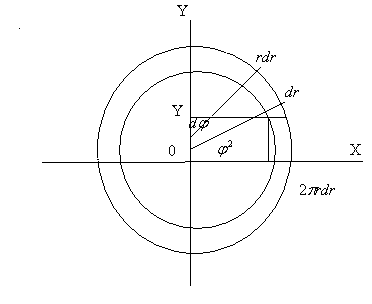
),онда аудан элементi dxdy-тiң орнына rdr.d
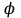
аламыз. Сонда, бiрқалыпты ықтималдық жағдайында
dw (r,φ) = C
 r dφ·dr
r dφ·drегер бiзге r –дiң модулi ғана қажет болса r =
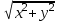 онда
ондабұрыш бойынша х интегралдау нəтижесiнде
dW (r)=
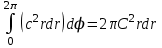
Ал, кеңiстiк үш өлшемдi болса, онда декарт координаттар
жүйесiнiң орнына сфералық жүйенi алуға болады (r,
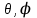 q,j):
q,j):X = r sin
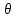 cos
cos
Y= r sin
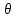 sin
sin
Z = r cos
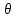
Ал көлем элементi dxdydz = dv орнына r
 sin
sin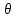 drd
drd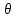 d
d болады. Ендi ықтималдық
болады. Ендi ықтималдықdW (z,
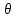 ,
, ) = const·r
) = const·r sin
sin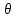 drd
drd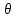 d
d
Егер кеңiстiктегi үлестiру
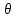 жəне
жəне  бұрыштарына тəуелдi болмаса
бұрыштарына тəуелдi болмасаdW(r)
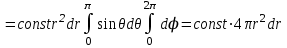
Статистикалық физика есептерiнде үлестiру функцияларының түрлерiн анықтау ең маңызды мiндеттерге жатады.
Мысал. Үлестірім заңымен берілген екі өлшемді кездейсоқ шаманы құраушыларының үлестірім заңдарын табыңыз.
Шешуі: ықтималдықтарды бағандар бойынша қосып, Х мүмкін мәндерінің ықтималдықтарын аламыз:
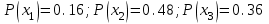
Х құраушысының үлестірім заңын жазайық:

Кесте2
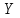 | Х | ||
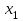 | 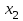 | 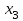 | |
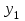 | 0,10 | 0,30 | 0,20 |
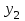 | 0,06 | 0,18 | 0,16 |
Бақылау: 0,16+0,48+0,36=1
Ықтималдықтары жолдар бойынша қосып, У мүмкін мәндерінің ықтималдықтарын аламыз:
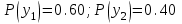 . У құраушысының үлестірім заңын жазайық:
. У құраушысының үлестірім заңын жазайық:Кесте3
| У | 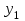 | 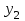 |
| Р | 0,60 | 0,40 |
Бақылау: 0,60+0,40=1.
Әдебиеттер:
 ,
, ,
, ,
,  , [10] §1, 14 тарау; [9], I тарау §1. [24], I тарау §1.
, [10] §1, 14 тарау; [9], I тарау §1. [24], I тарау §1.Өткізу формасы:топпен жұмыс.
Бағалау критерийлері:
| 90-100 | Есептердің орындалуының кем дегенде 90% - ның болуы (жазбаша) |
| 70-89 | Негізгі eceптерді шешу дағдыларын қалыптастыру (жаттығу eceптері) |
| 50-69 | Таңдап алынған әдістің берілген eceпті шығаруга тиімділігін болжауды білмейді |
| 0-49 | Есептің шығарылмауы немесе тіпті қате шығарылуы. |