Добавлен: 04.12.2023
Просмотров: 158
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
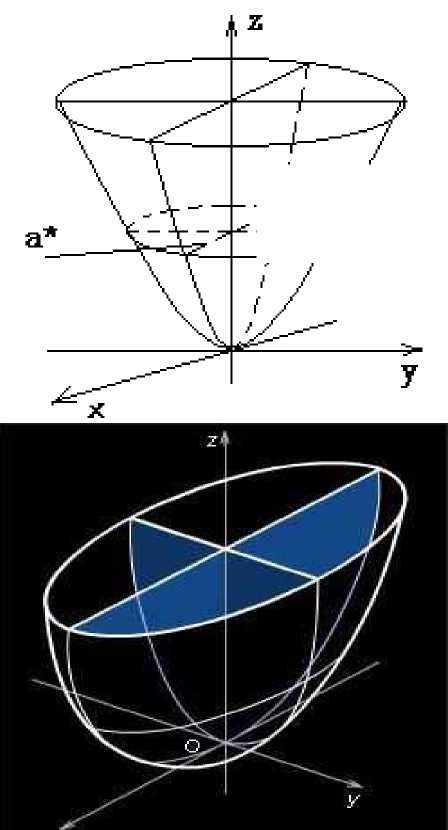
Эллиптический параболой
Эллиптическим параболоидом
называется поверхность,
которая в некоторой
прямоугольной системе
координат определяется
уравнением
ЦуП 2
IX + X = 2 ^ (7)
Где p>0 и q>0.
Уравнение(7) называется
каноническим уравнением
эллиптического параболоида.


Гиперболический
аболои
(9)
где p>0, q>0
Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением

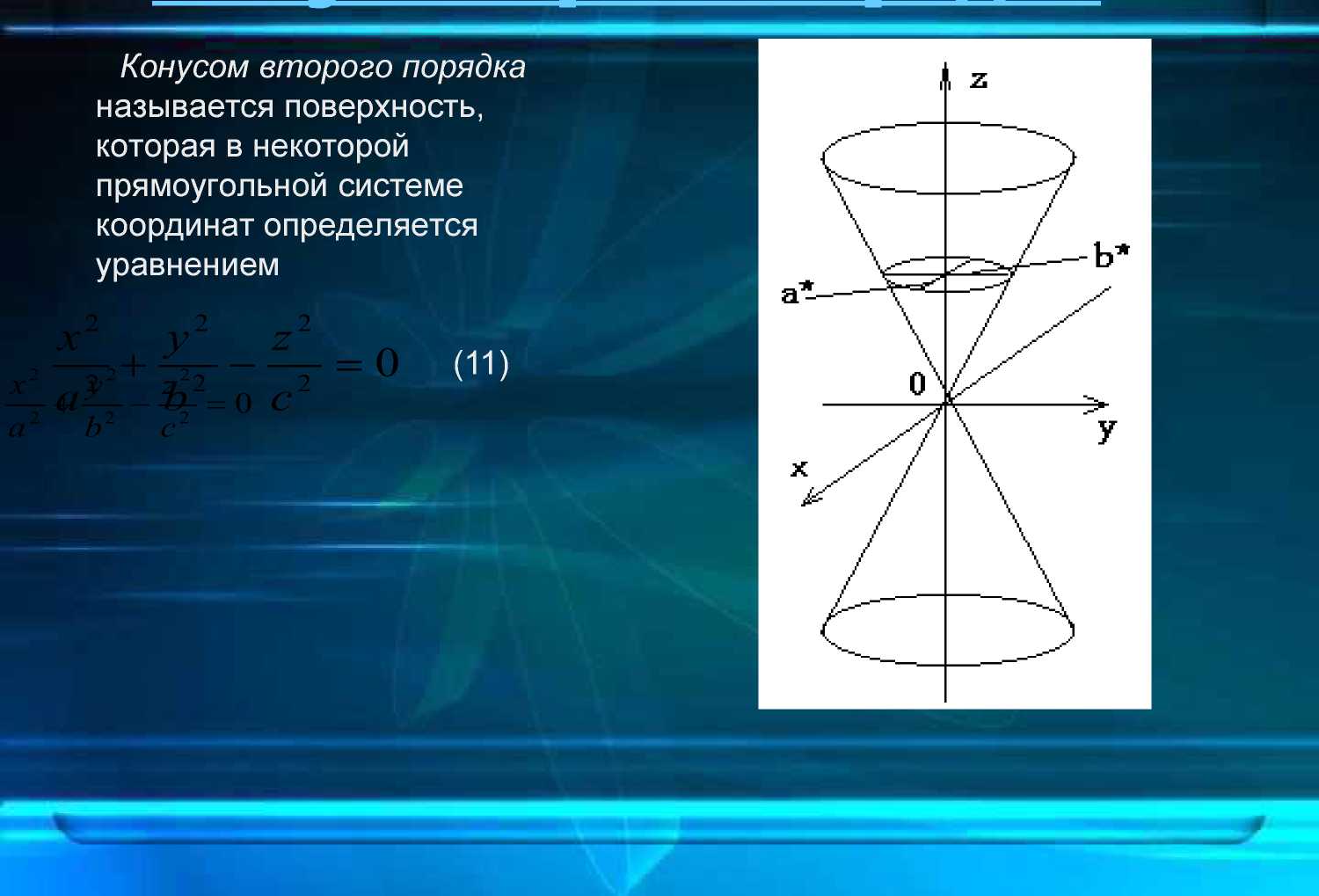
Конус второго порядка

Далеко не всякая поверхность, полученная вращением кривой второго порядка, является поверхностью второго порядка. Приведем пример.
Пример. Написать уравнение поверхности, образованной вращением параболы z2 — 2ру = 0, х = 0 вокруг оси Oz
Решение. В данном случае кривая не симметрична относительно оси вращения Oz, однако ординаты всех точек этой кривой неотрицательны, поэтому уравнение поверхности вращения имеет вид (2):
_ 2рух2 4- у® = о, или Z2= 2рVЛ'2
Если возвести обе части последнего равенства в квадрат, то получим уравнение поверхности в следующем виде:
z4 = 4р2 (х2 + у2). Легко видеть, что это уравнение эквивалентно предыдущему, поэтому в данном случае поверхность вращения является поверхностью четвертого порядка.
Уравнение сферической поверхности
Сферическая поверхность, или сфера, есть множество точек, равноудаленных от некоторой точки, называемой центром. Пусть в прямоугольной декартовой системе координат Oijk точка С (х0, у0, z0) является центром сферической поверхности радиуса г. Для того чтобы точка М (x, у, Z) принадлежала сферической поверхности, необходимо и достаточно, чтобы МС = r или
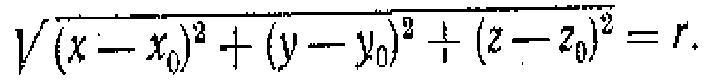
Возведём обе части уравнения в квадрат:
(х - Хо)2+ (у - Уо)2 + (z- Zo) = r2 (4)
_или в развернутом виде:
X2 + у2 + z2 - 2xox- 2УоУ - 2ZoZ+ Хо2 + Уо2 + Zo2 - r2 = 0. (5)
В частности, если точка С совпадает с началом координат, то уравнение сферы имеет вид:
x2+y2+z2=r2 (6)


Уравнение цилиндрической поверхности
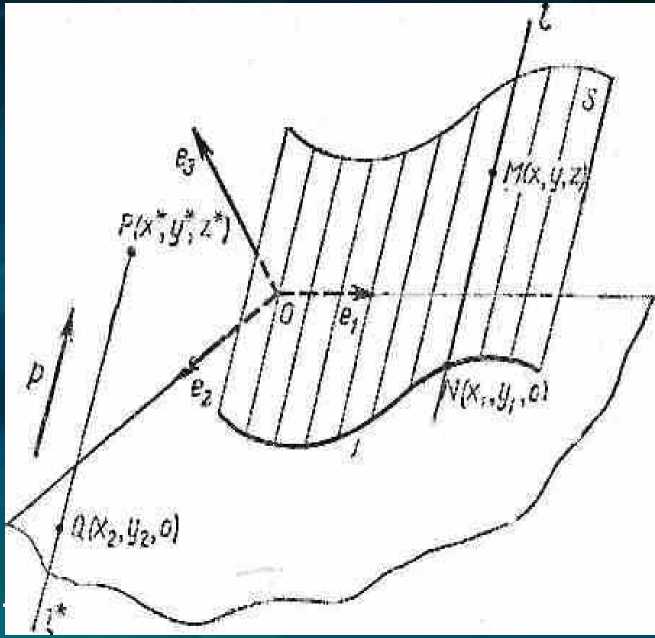
Рис. 182.
Поверхность, обладающая тем свойством, что
вместе с каждой точкой М она содержит всю
прямую, проходящую через М, параллельную
данному фиксированному
вектору р, называется цилиндрической
поверхностью или цилиндром.
Прямые, параллельные вектору р и
принадлежащие цилиндрической поверхности,
называются образующими этой поверхности.
Цилиндрическая поверхность может быть
образована следующим образом. Пусть L—
некоторая линия, а р — ненулевой вектор.
Поверхность, образованная прямыми,
проходящими через все точки линии L и
содержащими вектор р, будет цилиндрической
Прямые, содержащие вектор р, будут
образующими этой поверхности. В этом случае линия L называется направляющей этой поверхности (рис. 182).



Рис. 4.58. Касание поверхностей второго порядка в двух точках
Рис. 4.59. Построение круговых сечений на кривых поверхностях 2-го порядка
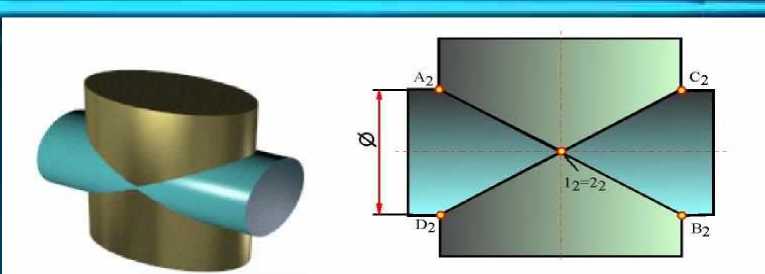
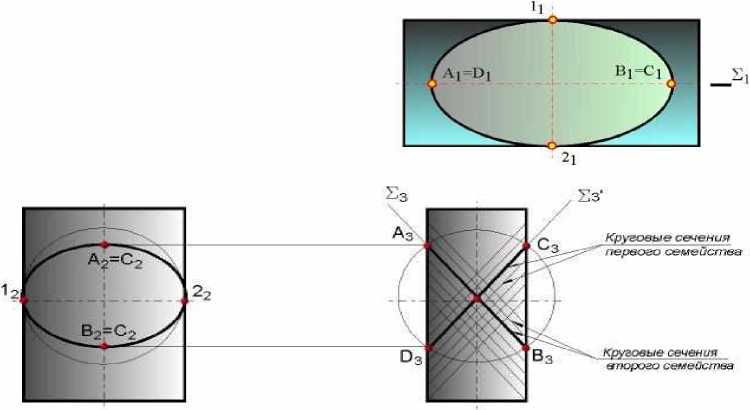
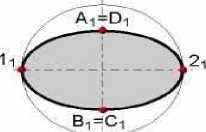
Теорема 1. Если две поверхности второго порядка имеют касание в двух точках (1 и 2 на рис. 4.58), то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания. Сфера, имеющая двойное касание с поверхностью второго порядка (рис. 4.59), может быть использована для нахождения круговых сечений тех поверхностей второго порядка, которые их имеют.
Г
Рис. 4.60. теорема Монжа 4.62 сфера пересекается с пирамидой
рис. 4.61 пересечение поверхностей сферы и эллиптического цилиндра
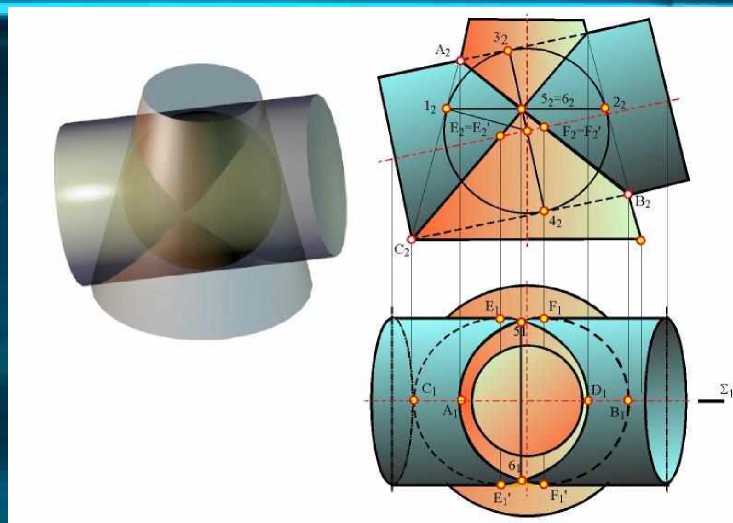
Теорема 2 (теорема Монжа).Если две
поверхности второго порядка описаны
около третьей или вписаны в неё(рис.
4.60), то линия их пересечения
распадается на две кривые второго
порядка, плоскости которых проходят
через прямую, соединяющую точки
пересечения линий касания
(прямая 5 - 6 ).
Теорема Монжа является частным
случаем теоремы 1.
4



Монж Гаспар (10.5.1746-28.7.1818)-
французский геометр и общественный
деятель, Член Парижской Академии Наук
(1780г.). Творец начертательной геометрии,
Монж дал обстоятельное изложение
дифференциальной геометрии
пространственных кривых и поверхностей:
изучил эволюты пространственных кривых,
кривизны поверхностей, исследовал
огибающие, развёртывающиеся поверхности и
т. д.
Монжу принадлежат также работы по
математическому анализу, химии, оптике,
метеорологии и практической механике.
V
вывод
Поверхности второго порядка - это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Для изучения формы поверхности пользуются так называемым методом сечений. Сущность этого метода заключается в следующем: поверхность S рассекается плоскостями, параллельными координатным плоскостям, и определяются линии пересечения поверхности с данными плоскостями. По виду этих линий судят о форме данной поверхности.
Некоторые поверхности могут быть образованны вращением некоторых кривых второго порядка (таких как эллипс, гипербола, парабола) - они называются поверхностями вращения. К ним относятся:
-
Эллипсоид. -
Однополостный гиперболоид. -
Двуполостный гиперболоид. -
Эллиптический параболоид. -
Гиперболический параболоид. -
Конус второго порядка
Существуют так же:
-
Сферические поверхности, или сферы - это множество точек, равноудаленных от некоторой точки, называемой центром. -
Цилиндрические поверхности или цилиндры, т. е. поверхности, обладающие тем свойством, что вместе с каждой точкой М она содержит всю прямую, проходящую через М, параллельную данному фиксированному вектору р. Прямые, параллельные вектору p и принадлежащие цилиндрической поверхности, называются образующими этой поверхности.

V
Список литературы
1. «Аналитическая геометрия» В.А. Ильин, Э.Г. Позняк
2. «Аналитическая геометрия» Л.С.
Атанасян