Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

КАФЕДРА ДИАГНОСТИЧЕСКИХ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Типовой расчет.
по дисциплине

Метрология информационно-измерительных систем
Выполнил студент:

Дроздов А.С.

Группа А-04м-22

Принял:

доцент Долгачева Е.А.
Москва 2022

Задание МИС_Рз2-4.

Рассчитать цифровой фильтр Баттерворта верхних частот восьмого порядка с частотой среза f_с = 100 Гц.

Необходимо:

1. Выбрать структурную схему фильтра и частоту дискретизации f_д.

2. Пояснить порядок работы схемы фильтра.

3. Найти аналитическое выражение для амплитудно-частотной характеристики фильтра A(f ) и построить её график.

1. Выбрать структурную схему фильтра и частоту дискретизации fд.

Структурная схема фильтра показана на рисунке 1.



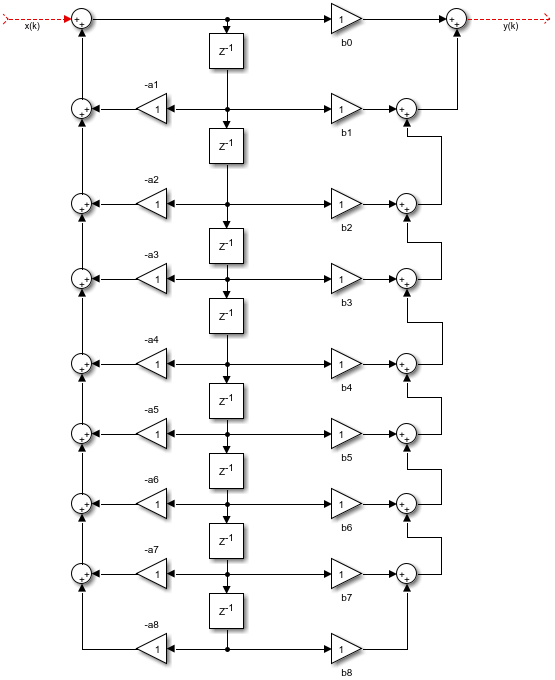
Рисунок 1. Структурная схема

Частота дискретизация выбрана в 2 раза больше, чем частота среза , 200 Гц.

2. Пояснить порядок работы схемы фильтра.

Задержка дискретной последовательности на один такт – это произведение z на z-1 (свойства z-преобразования). На структурной схеме такие элементы обозначаются как z-1. Порядок фильтра ­– это количество предыдущих отсчетов в схеме.

Предыдущие отсчеты сигнала хранятся в ячейках памяти, образующие дискретную линию задержки. Эти отсчеты умножаются на коэффициенты bk и ak и суммируются, формируя выходной отсчет y(n).
3. Найти аналитическое выражение для амплитудно-частотной характеристики фильтра A(f ) и построить её график.

---

Нахождение аналитического выражения и построение графика АЧХ выполнено в программе Matlab

clear, clc

N = 7; % Порядок фильтра

fc = 1000; % Частота среза

fs = 2000; % Частота дискретизации, выбрана как fc*2, частота Найквиста

Rp = 0.01; % Неравномерность в полосе пропускания

% Rs = 30; % Уровень подавления в полосе заграждения

wp = pi*fc/fs; % Нормированная частота среза

T = 2; % Интервал дискретизации

syms s z w; % Символьные переменные

Wp = tan(wp/2); % Расчет частоты среза аналогового фильтра

eps_p = sqrt(power(10, Rp/10)-1);

% eps_s = sqrt(power(10, Rs/10)-1);

% Ws = power(10, log(eps_s/eps_p)/N)*Wp

L = floor(N/2);

r = N-2*L;

alpha = 1/(power(eps_p, 1/N))

alpha = 1.5430

% Расчет передаточной характеристики аналогового нормированного ФВЧ

% Цикл расчета произведения

prod = 1;

for i = 1:L

teta = (2*i-1)/(2*N)*pi;

prod = prod*(s^2+2*alpha*sin(teta)*s+alpha^2);

end

Hh(s) = 1/(eps_p*(s+alpha)^r*prod); % Передаточная характеристика нормированного ФВЧ

vpa(Hh(s), 2)

ans = 



% Частотное преобразование передаточной характеристики аналогового нормированного ФВЧ

Hh1(s) = Hh(Wp/s);

vpa(Hh1(s), 2)

ans = 



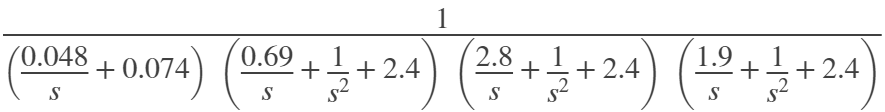
% Расчет передаточной характеристики цифрового фильтра

Hh2(z) = Hh1((2/T)*(1-z^-1)/(1+z^-1)); % Билинейное преобразование

vpa(Hh2(z), 2)

ans = 



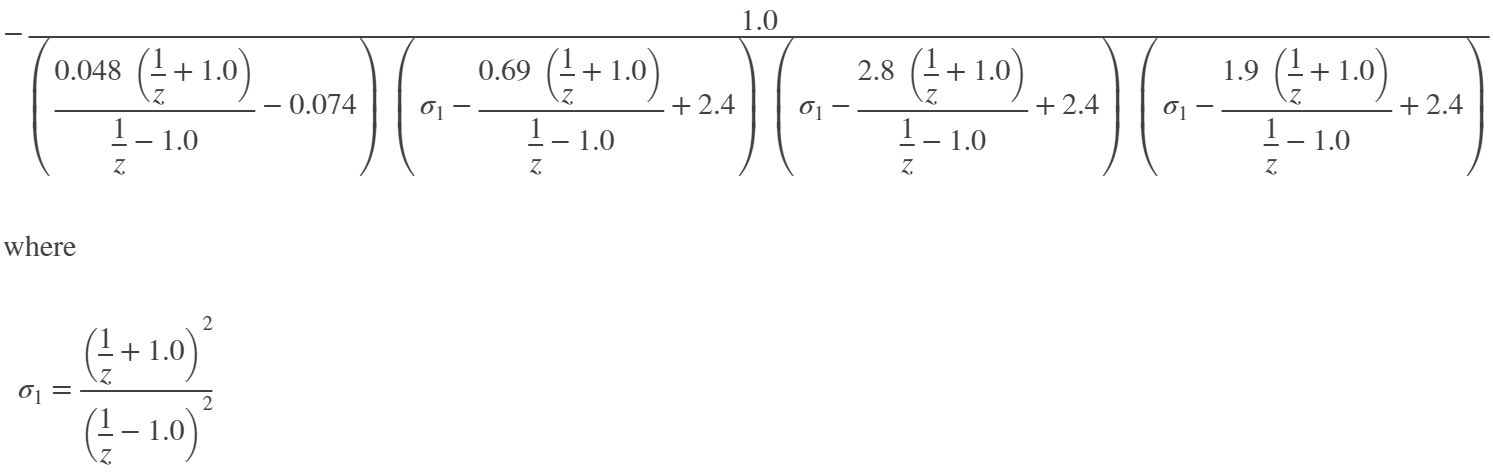
% Расчет АЧХ фильтра

w = 0.01:0.01:pi;

fq = double(abs(Hh2(exp(1i*w))).^2);

f = fs/length(w):fs/length(w):fs;

figure

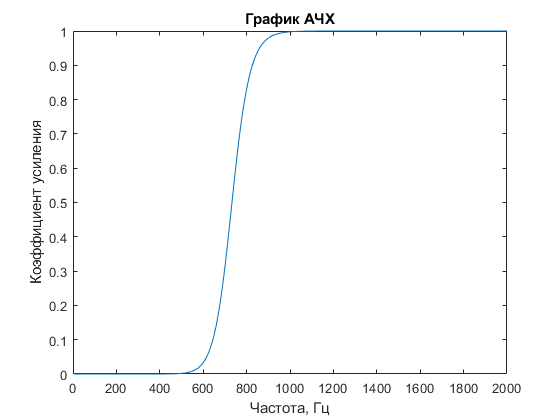
plot(f, fq)

title('График АЧХ')

xlabel('Частота, Гц')

ylabel('Коэффициент усиления')

---

Смотрите также файлы

• Выписка из Положения 10. Структура и объем выпускных квалификационных работ (вкр).docx

• Пояснительная записка выполняется на листах формата объем пояснительной записки должен составлять 5055 страниц.docx

• Отчёт по производственной практике по модулю ПМ. 04 Взаимодействие с родителями (лицами, их заменяющими) и сотрудниками образовательной организации (учреждения) (летняя в доу).docx

• Разночинец, рантье, метис, горожанин, пенсионер, ребенок.docx

• Подготовьте сообщение о научной деятельности сурдопедагогов xixxx веков.docx