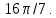ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 89
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Институт химии и энергетики
| (наименование института полностью) |
| Институт химии и энергетики |
| (Наименование учебного структурного подразделения) |
| 13.03.02 Электроэнергетика и электротехника |
| (код и наименование направления подготовки / специальности) |
| Электроснабжение |
| (направленность (профиль) / специализация) |
Практическое задание №5
по учебному курсу «Высшая математика 2»
(наименование учебного курса)
Вариант 1 (при наличии)
| Обучающегося | Аитбаев Ильдар Мурзагильдиевич | |
| | (И.О. Фамилия) | |
| Группа | ЭЭТбд-2101а | |
| | | |
| Преподаватель | Крылова Светлана Александровна | |
| | (И.О. Фамилия) | |
Тольятти 2023
Задача 1. Вычислить объём тела, заданного представленными уравнениями,
используя его поперечные сечения
Вариант 1.
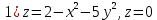
Решение. Построим рисунок поверхности, используя какой-нибудь онлайн сервис, например 3D Calculator - GeoGebra
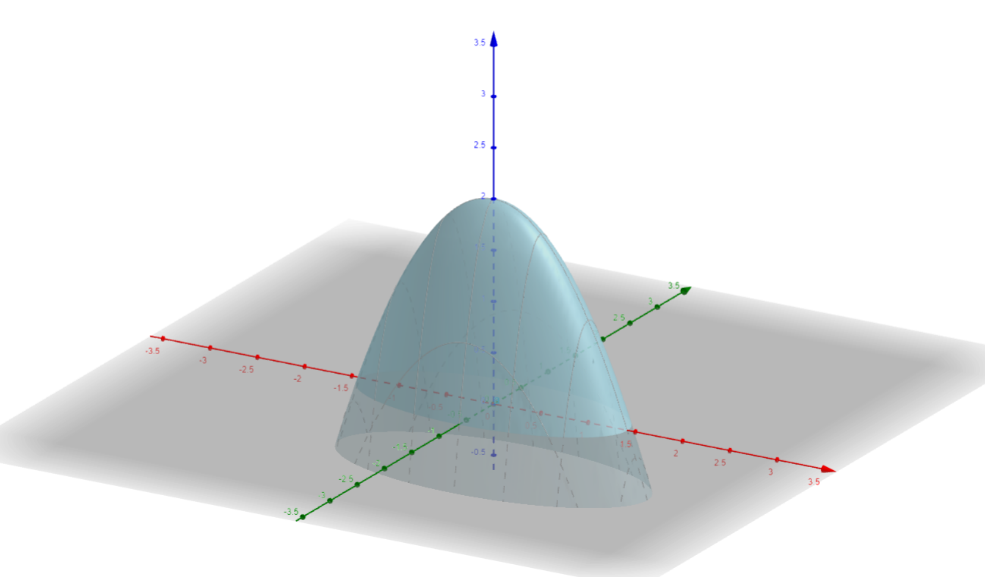
Рисунок 1. Заданная поверхность
Мы видим, что искомый объем нахрдится под куполом, заданным первым уравнением
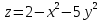, и снизу ограничен плоскостью 
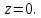Найдем пересечение поверхности с плоскостью, то есть: 
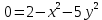, или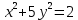 
, окончательно получаем уравнение эллипса: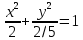
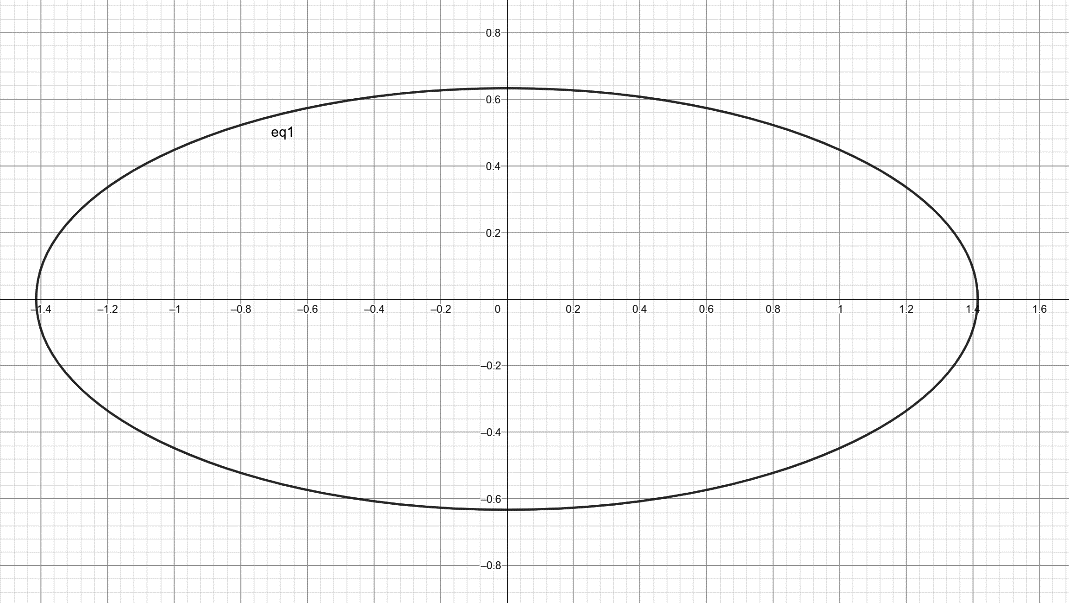
Рисунок 2. Линия пересечения
Таким образом, когда переменные
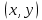меняются в пределах этого эллипса, переменная 
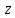меняется в пределах от 0 до поверхности 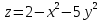.Введем новые переменные:
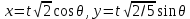
Тогда новые переменные изменяются в следующих пределах:
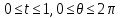
А переменная
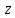, соответственно, от плоскости основания, до поверхности («купола»):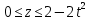
Таким образом, объем вычисляется как тройной интеграл:
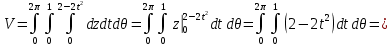
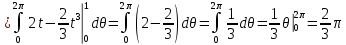
Ответ:
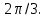
Задача 2. Вычислить объём тела, образованного вращением вокруг оси
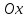фигуры, заданной представленными линиямиВариант 1.
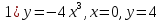
Решение. Построим поверхность вращения.
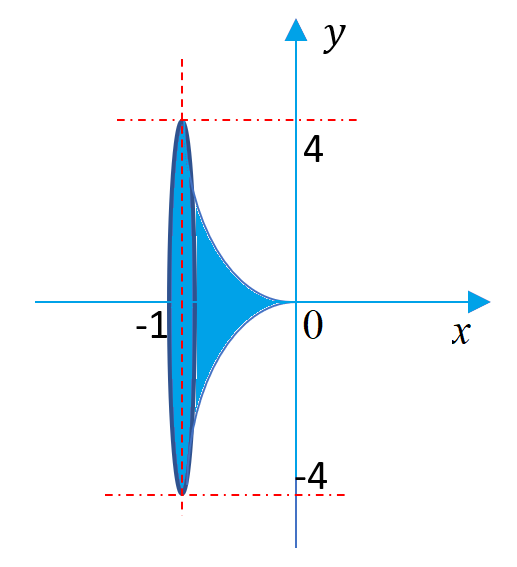
Рисунок 3. Фигура вращения
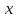меняется в пределах от -1 до 0. Таким образом, объем получаем по формуле: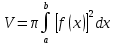
В нашем случаем,
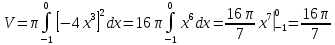
Ответ:
