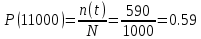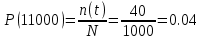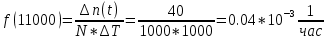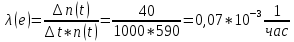ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа по дисциплине: Надежность информационных систем
Выполнена: Полетаевым Егором Руслановичем
студентом группы ИСз-218
направление подготовки: 09.03.02 Информационные системы и технологии
преподаватель: Куралесин Вячеслав Викторович.
Практическая работа № 1.
Тема: Расчет показателей надежности не резервированных
не восстанавливаемых систем.
Задача 1.
На испытание поставлено N = 400 изделий. За время t = 3000 час отказало 200 изделий, т.е. n(t) = 400 – 200 = 200. За интервал времени ∆t, где t = 100 час, отказало 100 изделий, т.е. n(t) = 100. Требуется определить Р(3000), P(3100), f (3000), λ(3000).
Решение.
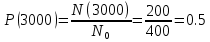
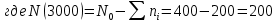
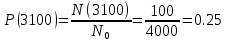
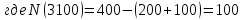
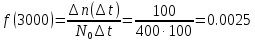
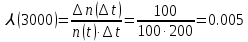
Задача 2.
На испытание поставлено 100 однотипных изделий. За 4000 час отказало 50 изделий. За интервал времени 4000 - 4100 час отказало ещё 20 изделий. Требуется определить f(t), λ(t) при t = 4000 час.
Решение.
В данном случае N=100; t=4000 час; Δt =100 час; Δn(t)=20; n(t)=50.
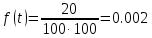
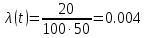
Задача 3. На испытание поставлено 100 однотипных изделий. За 4000 час отказало 50 изделий. Требуется определить P0(t) и Q0 (t) при t = 4000 час.
Решение.
В данном случае N= 100; n(t)=100-50=50; N-n(t)=100-50=50. По формулам определяем:
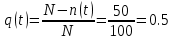
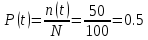
Задача 4.
В течение 1000 час из 10 гироскопов отказало 2. За интервал времени 1000 - 1100 час отказал еще один гироскоп. Требуется определить f(t), λ(t) при t =1000 час.
Решение.
В данном случае N=10; t=1000 час; Δt =100 час; Δn(t)=1; n(t)=8.
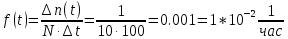
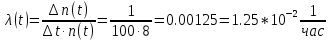
Задача 5.
На испытание поставлено 1000 однотипных электронных ламп. За первые 3000 час отказало 80 ламп. За интервал времени 3000 – 4000 час отказало еще 50 ламп. Требуется определить P0(t) и Q0 (t) при t = 4000 час.
Решение.
В данном случае N= 1000; n(t)=1000-80-50=870; N-n(t)=1000-870=130.
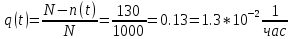
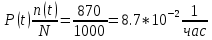
Задача 6.
На испытание поставлено 1000 изделий. За время t = 1300 час вышло из строя 288 штук изделий. За последующий интервал времени 1300-1400 час вышло из строя еще 13 изделий. Необходимо вычислить P0(t) при t = 1300 час и t =1400 час; f(t), λ(t) при t =1300 час.
Решение.
В данном случае N=1000; t=1300 час; Δt =100 час; Δn(t)=13; n(t)=288; n(1300)=1000-288=712; n(1400)=1000-288-13=699
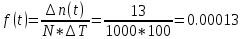
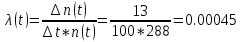
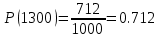
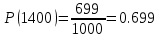
Задача 7.
На испытание поставлено 45 изделий. За время t = 60 час вышло из строя 35 штук изделий. За последующий интервал времени 60-65 час вышло из строя еще 3 изделия. Необходимо вычислить P0(t) при t = 60час и t = 65 час; P0(t) при t = 60 час.
Решение.
В данном случае N=45; t=60 час; Δt =5 час; Δn(t)=3; n(t)=35; n(60)=45-35=10; n(65)=45-35-3=7.
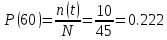
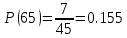
Задача 8.
В результате наблюдения за 45 образцами радиоэлектронного оборудования, которые прошли предварительную 80 - часовую приработку, получены данные до первого отказа всех 45 образцов, сведенные в табл.1.2. Необходимо определить mt.
| ti, час | ni | ti, час | ni | ti, час | ni |
| 0-10 | 19 | 30-40 | 3 | 60-70 | 1 |
| 10-20 | 13 | 40-50 | 0 | | |
| 20-30 | 8 | 50-60 | 1 | | |
Таблица 1.
Решение.
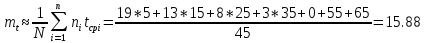
Задача 9.
На испытание поставлено 8 однотипных изделий. Получены следующие значения ti (ti - время безотказной работы i-го изделия): t1 = 560 час; t2 = 700 час; t3 = 800 час; t4 = 650 час; t5 = 580 час; t6 = 760 час; t7 = 920 час; t8 = 850час. Определить статистическую оценку среднего времени безотказной работы изделия.
Решение.
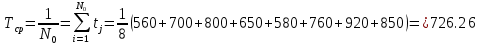
Статистическая оценка среднего времени безотказной работы.
Задача 10.
За наблюдаемый период эксплуатации в аппаратуре было зарегистрировано 6 отказов. Время восстановления составило: t1 = 15мин; t2 = 20 мин; t3 = 10 мин; t4 = 28 мин; t5 = 22 мин; t6 = 30 мин. Требуется определить среднее время восстановления аппаратуры mtâ .
Решение.
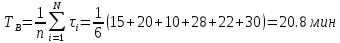
Получаем среднее время восстановления аппаратуры.
Задача 11.
На испытание поставлено 1000 изделий. За время t = 11000 час вышло из строя 410 изделий. За последующий интервал времени 11000- 12000 час вышло из строя еще 40 изделий. Необходимо вычислить P0(t) при t = 11000 час и t = 12000 час, а также f(t), λ(t) при t = 11000 час.
Решение.
N=1000, T=11000час, Δt=1000час, n(t)=(1000-410)=590, Δn(t)=40.