Файл: Задание 1. Методом изоклин построить интегральные уравнения.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 8

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Автономная некоммерческая организация высшего образования

«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления
Форма обучения: заочная


ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Математика



Группа 22М571в

Студент
В.С. Филатова


МОСКВА 2023

ТЕМА №13

Задание №1. Методом изоклин построить интегральные уравнения.



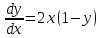
Если принять 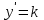, то уравнение изоклины для заданного уравнения: 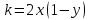или 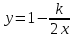– уравнение гипербол. Для примера ограничимся значениям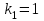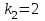и: , и .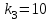

Построим интегральные кривые, пересекающие каждую из гипербол-изоклин под определённым углом: первую под углом, определяемым угловым коэффициентом 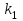, вторую под углом, определяемым угловым коэффициентом 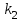и третью под углом, определяемым угловым коэффициентом .

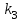Сделаем чертеж:



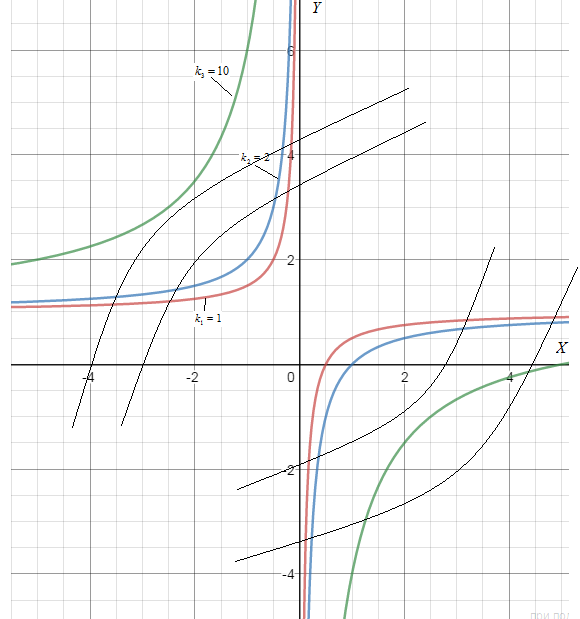
Ответ: на рисунке показаны интегральные кривые.

Задание №2. Решитьуравнения
, допускающие понижение порядка



























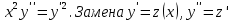
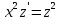
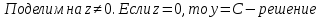
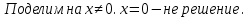
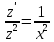
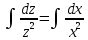
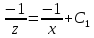
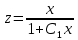
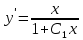
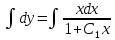
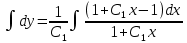
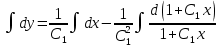
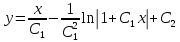
Ответ: ,


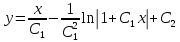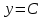
Задание № 3. Решить систему уравнений


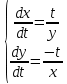
Решение:

Решаем методом подстановки:






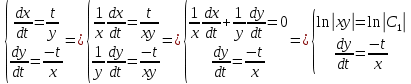
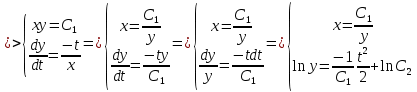
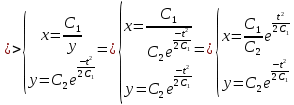
Ответ:

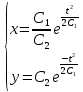
Задание №4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10?

Решение

Если производится 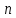независимых испытаний, при каждом из которых вероятность осуществления события 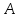постоянна и равна 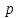, а вероятность противоположного события равна 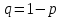, то число успехов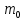
, при котором достигается наибольшая из возможных вероятностей, определяется как целое число на промежутке по формуле:



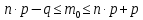
Для данного случая













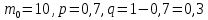
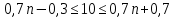
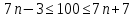
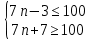
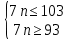
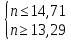
Поскольку – целое число, то .

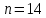Ответ:

Смотрите также файлы