Файл: Проведено тестирование студентов вгспу по следующим показателям.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 35
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Проведено тестирование студентов ВГСПУ по следующим показателям:
| № | F кист | F стан | H, см | балл | место | |||
| Рез-т | балл | Рез-т | балл | Рез-т | балл | | | |
| 1 | 45 | 48,06 | 140 | 50,00 | 43 | 40,51 | 138,56 | 4 |
| 2 | 44 | 46,12 | 155 | 58,48 | 47 | 53,16 | 157,77 | 2 |
| 3 | 55 | 67,48 | 160 | 61,31 | 45 | 46,84 | 175,62 | 1 |
| 4 | 42 | 42,23 | 120 | 38,69 | 44 | 43,67 | 124,59 | 5 |
| 5 | 44 | 46,12 | 125 | 41,52 | 51 | 65,82 | 153,46 | 3 |
Определить личный результат в баллах по каждому из предлагаемых тестов, применив стандартную Т-шкалу. Распределить места по сумме баллов в каждом тесте и занести в таблицу. Представить результаты тестирования в графической форме (профиле подготовленности)
Разработать нормы оценок для избранной совокупности
F кист
| № | Xi | Хi- 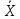 | (Хi- 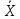 )² )² |
| 1 | 45 | -1 | 1 |
| 2 | 44 | -2 | 4 |
| 3 | 55 | 9 | 81 |
| 4 | 42 | -4 | 16 |
| 5 | 44 | -2 | 4 |
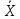 | 46 | | Ʃ= 106 |
 =(45+44+55+42+44)/5=46
=(45+44+55+42+44)/5=46σ=
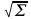 (Хi-
(Хi- )²/n-1=
)²/n-1=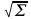 106/4=5,15
106/4=5,15Т=50+10* Хi-
 / σ
/ σТ1=50+10*(-1)/5,15=48,06
Т2=50+10*(-2)/5,15=46,12
Т1=50+10*9/5,15=67,48
Т1=50+10*(-4)/5,15=42,23
Т1=50+10*(-2)/5,15=46,12
F стан
| № | Xi | Хi-  | (Хi-  )² )² |
| 1 | 140 | 0 | 0 |
| 2 | 155 | 15 | 225 |
| 3 | 160 | 20 | 400 |
| 4 | 120 | -20 | 400 |
| 5 | 125 | -15 | 225 |
 | 140 | | Ʃ= 1250 |
 =(140+155+160+120+125+140)/5=140
=(140+155+160+120+125+140)/5=140σ=
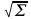 (Хi-
(Хi- )²/n-1=
)²/n-1=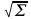 1250/4=17,68
1250/4=17,68Т=50+10* Хi-
 / σ
/ σТ1=50+10*(0)/17,68=50
Т2=50+10*15/17,68=58,48
Т1=50+10*20/17,68=61,31
Т1=50+10*(-20)/17,68=38,69
Т1=50+10*(-15)/17,68=41,52
H, см
| № | Xi | Хi-  | (Хi-  )² )² |
| 1 | 43 | -3 | 9 |
| 2 | 47 | 1 | 1 |
| 3 | 45 | -1 | 1 |
| 4 | 44 | -2 | 4 |
| 5 | 51 | 5 | 25 |
 | 46 | | Ʃ= 40 |
 =(43+47+45+44+51)/5=46
=(43+47+45+44+51)/5=46σ=
 (Хi-
(Хi- )²/n-1=
)²/n-1= 40/4=3,16
40/4=3,16Т=50+10* Хi-
 / σ
/ σТ1=50+10*(-3)/ 3,16=40,51
Т2=50+10*1/ 3,16=53,16
Т1=50+10*(-1)/3,16=46,84
Т1=50+10*(-2)/ 3,16=43,67
Т1=50+10*5/ 3,16=65,82
Профиль подготовленности для спортсменов
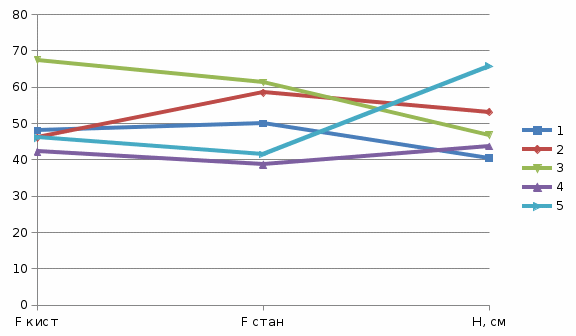
Вариант 1. Для совершенствования методики педагогического контроля физической подготовленности тяжелоатлетов изучалась взаимосвязь отдельных упражнений со спортивным результатом
Прыжок в высоту с места, см (Х)
Спортивный результат в толчке, кг (Y)
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Х | 57 | 60 | 58 | 61 | 63 | 58 | 55 | 64 | 65 | 64 | 66 | 61 |
| Y | 107,5 | 110 | 110 | 115 | 115 | 107,5 | 107 | 120 | 122,5 | 112,5 | 120 | 110 |
Представь результаты тестирования в графической форме (построить корреляционное поле), проанализировать график
Выбрать метод расчета коэффициента корреляции. Установить тесноту взаимосвязи. Оценить достоверность статистической взаимосвязи результатов
Составить уравнение регрессии Y на X и X на Y
Определить какой результат в толчке покажет штангист, если он прыгнет на 71 см
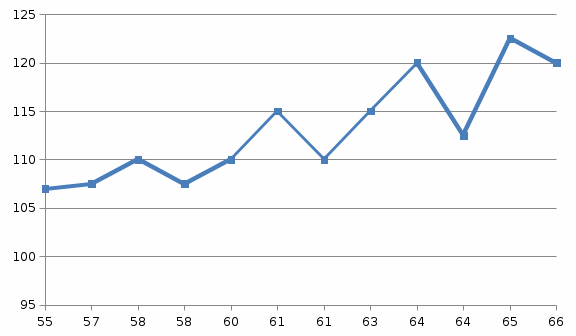
Таким образом у нас положительная прямо пропорциональная сильная взаимосвязь
Расчет коэффициента корреляции Бравэ — Пирсона
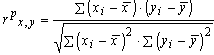
R=183/
 134*319,9=0,88
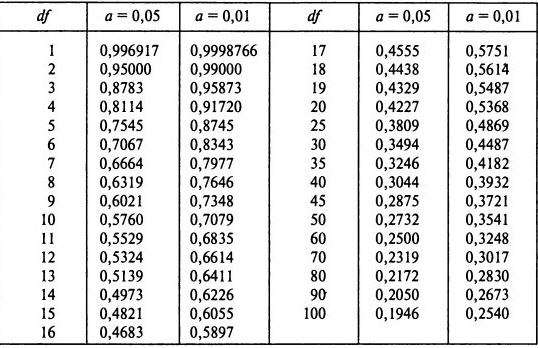
134*319,9=0,88Если полученное значение коэффициента корреляции превосходит табличное значение при заданном уровне значимости (r > rкрит), то наличие связи между результатами в прыжках в высоту с места и спортивном результате в толчке можно считать достоверным. По таблице (приложение) находим критическое значение при n=12-2=10. Это значение равно 0,71, следовательно, мы имеем неравенство r > rкрит (0,88 > 0,71), поэтому проявление связи достоверно (r= 0,88 при Р < 0,01). Это значит, что улучшение результата в прыжках в высоту с места связано с улучшением спортивного результата в толчке
Коэффициента детерминации (D), который вычисляют по формуле: D = r2*100 %.
D =0,88^2*100%=77,4
Следовательно, 77,4% взаимосвязи спортивных результатов объясняется их взаимовлиянием. Остальная часть вариации (100 % − 77,4 % = 22,6 %) объясняется влиянием других неучтенных факторов
| № | X | Y | Хi-  | (Yi- 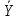 ) ) | (Хi-  )*(Yi- )*(Yi-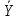 ) ) | (Хi-  )² )² | (Yi- 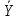 )² )² |
| 1 | 57 | 107,5 | -4 | -5,6 | 22,4 | 16 | 31,36 |
| 2 | 60 | 110 | -1 | -3,1 | 3,1 | 1 | 9,61 |
| 3 | 58 | 110 | -3 | -3,1 | 9,3 | 9 | 9,61 |
| 4 | 61 | 115 | 0 | 1,9 | 0 | 0 | 3,61 |
| 5 | 63 | 115 | 2 | 1,9 | 3,8 | 4 | 3,61 |
| 6 | 58 | 107,5 | -3 | -5,6 | 16,8 | 9 | 31,36 |
| 7 | 55 | 107 | -6 | -6,1 | 36,6 | 36 | 37,21 |
| 8 | 64 | 120 | 3 | 6,9 | 20,7 | 9 | 47,61 |
| 9 | 65 | 122,5 | 4 | 9,4 | 37,6 | 16 | 88,36 |
| 10 | 64 | 112,5 | 3 | -0,6 | -1,8 | 9 | 0,36 |
| 11 | 66 | 120 | 5 | 6,9 | 34,5 | 25 | 47,61 |
| 12 | 61 | 110 | 0 | -3,1 | 0 | 0 | 9,61 |
| Ʃ | 732 | 1357 | | | 183 | 134 | 319,92 |
| Х | 61 | 113,1 | | | | | |
σ=
 (Хi-
(Хi- )²/n-1
)²/n-1σх=
 134/11=3,49
134/11=3,49σy=
 319,92/11=5,39
319,92/11=5,39Исходя из представлений о корреляционной зависимости, уравнения регрессии при линейной взаимосвязи будут иметь следующий вид:
У= а1+ bу/хґ Х
Х = а2+ bх/уґ у
В первом уравнении величина У изменяется в зависимости от величины Х. Во втором уравнении наоборот: величина Х изменяется в зависимости от величины У.
Вычислим так называемый коэффициент регрессии. Так, если уже проводился корреляционный анализ, то коэффициенты bх/у и bу/х вычисляются по следующим формулам:
| | by/x r | y | 0,88* | 5,39 | =1,36 | |
| | | x | | 3,49 | | |
| | bx/y r | x | 0,84 | | 3,49 | =0,57 |
| | y | 5,39 | ||||
| | | | | |||
Коэффициенты а1 и а2 рассчитываются по формулам:
а1 = Y - bу/х *Х= 113,1 – 1,36 *61=30,14
а2 = X - bх/у Ч = 61 – 0,57 *113,1 = -3,467
У = ? Х = 71 см
У= а1 + bу/х ґ Х
У = 30,14 + 1,36 × 71 = 126,7
Таким образом, при прыжке71 см результат в толчке будет 126,7