Файл: Лабораторная работа 1 по теме Методы решения нелинейных уравнений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 121
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа №1
по теме
«Методы решения нелинейных уравнений»
1.1. Вопросы, подлежащие изучению
-
Постановка задачи численного решения нелинейных уравнений. -
Этапы численного решения уравнения. -
Аналитический и графический методы отделения корней. -
Уточнение корня методами половинного деления, итерации, Ньютона и хорд. -
Графическая иллюстрация методов половинного деления, итерации, Ньютона и хорд. -
Условие окончания вычислений при использовании методов половинного деления, итерации, Ньютона и хорд. -
Сходимость метода итерации, выбор начального приближения, правило выбора итерирующей функции и оценка погрешности метода итерации. -
Теорема о сходимости метода Ньютона и оценка погрешности метода. -
Правило выбора неподвижной точки, начальной точки и условие сходимости метода хорд. -
Условия окончания вычислений в методах итерации, Ньютона и хорд. -
Сравнение методов половинного деления, итерации, Ньютона и хорд.
1.2. Общее задание
-
Выбрать индивидуальное задание из табл. 1-1:
-
нелинейное уравнение; -
методы решения нелинейного уравнения для выполнения 3-х итераций;
-
Отделить корни заданного уравнения графическим и аналитическим методом с использованием средств пакета Scilab. -
Для каждого из заданных методов провести исследование функции нелинейного уравнения:
-
проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости; -
выбрать начальное приближение к корню; -
сформулировать условие окончания этапа уточнения корня.
-
С использованием итерационной формуле 1-го заданного методу провести расчет трех итераций с использованием средств мат. пакета. Результаты расчета свести в табл. 1-2. -
Оценить погрешность результата после 3-х итераций. -
Для 2-го заданного метода выполнить решение уравнения с точностью 10-4, создав программу, реализующую заданный метод. Произвести расчет, а результаты решений свести в табл. 1-2. -
Найти решение нелинейного уравнения на отделенном отрезке с использованием функции fsolve пакета Scilab.
1.3. Варианты задания
Таблица 1-1
| № | Уравнение | 1-й метод | 2-й метод | № | Уравнение | 1-й метод | 2-й метод |
| 1 | x - cos(x / 3) = 0 | 1 | 4 | 16 | sin(1 – 0.2x2) – x = 0 | 3 | 4 |
| 2 | x + ln(4x) – 1 = 0 | 3 | 1 | 17 | ex – e-x – 2 = 0 | 2 | 1 |
| 3 | ex – 4 e-x – 1 = 0 | 2 | 4 | 18 | x – sin(1 / x) = 0 | 4 | 1 |
| 4 | x ex – 2 = 0 | 3 | 2 | 19 | ex + ln(x) – x = 0 | 1 | 2 |
| 5 | 4 (x2 + 1) ln(x) – 1 = 0 | 1 | 3 | 20 | 1–x+sin(x)–ln(1+x) = 0 | 1 | 3 |
| 6 | 2 – x – sin(x / 4) = 0 | 4 | 1 | 21 | (1–x)1/2–cos(1–x) = 0 | 4 | 1 |
| 7 | x2 + ln(x) – 2 = 0 | 1 | 2 | 22 | sin(x2)+cos(x2)–10x = 0 | 3 | 2 |
| 8 | cos(x)–(x + 2)1/2 + 1 = 0 | 2 | 3 | 23 | x2 – ln(1 + x) – 3 = 0 | 2 | 3 |
| 9 | 4 (1 + x1/2) ln(x) – 1 = 0 | 2 | 1 | 24 | cos(x / 2) ln(x – 1) = 0 | 1 | 2 |
| 10 | 5 ln(x) – x1/2 = 0 | 2 | 3 | 25 | cos(x/5) (1+x)1/2–x = 0 | 1 | 3 |
| 11 | ex + x3 – 2 = 0 | 1 | 4 | 26 | 3x – e-x = 0 | 4 | 2 |
| 12 | 3 sin (x1/2) + x – 3 = 0 | 3 | 1 | 27 | 4(1+x1/2) ln(x)–10 = 0 | 1 | 3 |
| 13 | 0.1x2 – x ln(x) = 0 | 1 | 4 | 28 | sin(x)–31/2cos(x)+4x–4 = 0 | 3 | 4 |
| 14 | cos(1 + 0.2x2) – x = 0 | 1 | 3 | 29 | x – 1 / (3 + sin(3.6x)) = 0 | 1 | 3 |
| 15 | 3 x – 4 ln(x) – 5 = 0 | 1 | 2 | 30 | 0.25x3 + cos(x / 4) = 0 | 4 | 2 |
В табл. 1-1 номера методов: 1 – половинное деление;2 – итерации;3 – Ньютона; 4 – хорд.
1.4. Содержание отчета
-
Индивидуальное задание (уравнение, методы для выполнения 3-х итераций). -
Результат отделения корней (график функции, таблица значений функции и её производных, вывод об отделённом отрезке, содержащем один корень). -
Результаты исследования функции уравнения для проведения расчетов. Привести для каждого метода:
-
условие сходимости вычислительного процесса; -
начальное приближение; -
условие окончания этапа уточнения корня.
-
В сценарии мат. пакета создать функции для проведения расчета 1-м методом. Результаты расчета по каждому методу свести в табл. 1-2.
Таблица 1-2
| к | x | f(x) |
| 1 | | |
| 2 | | |
| 3 | | |
| 4 | | |
-
Оценки погрешностей результатов расчетов после 3-х итераций с использованием формулы, соответствующего метода. -
Создать программу для решения уравнения 2-м заданный методом с точностью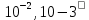 10-4. Построить график зависимости количества итераций от точности в логарифмическом масштабе.Решение нелинейного уравнения с использованием функции fsolve.
10-4. Построить график зависимости количества итераций от точности в логарифмическом масштабе.Решение нелинейного уравнения с использованием функции fsolve.
1.5. Пример выполнения задания с использованием мат. пакета MathCad
-
Решить уравнение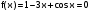 ;
; -
методы решения нелинейных уравнений – половинного деления, итерации, Ньютона и хорд;
Этап отделения корней.
Используем для этого математический пакет MathCad. Отделение корней произведем как графическим методом (график функции), так и аналитически (таблица).
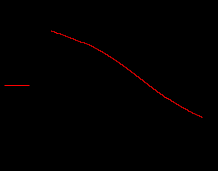     |
Рис.1. Графическое и аналитическое отделение корней уравнения.
Из построенного графика функции f(x) видно, что на отрезке (0, 1) есть один корень. На этом графический способ отделения корней заканчивается.
Другой вариант отделения корня – решить задачу аналитически.
Для аналитического отделения корня построена таблица рис.1. Она требует пояснений. В столбцах таблицы выведены некоторые значения аргумента x на заданном отрезке, а также значения функций f(x),
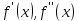 при этих значениях x.
при этих значениях x. Видно, что на отрезке (0, 1) функция f(x) меняет знак, значит существует, по крайней мере, один корень.
Значения первой производной
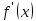 в заданных точках отрезка (0, 1) не меняет знак, что вызывает некоторую надежду о том, что
в заданных точках отрезка (0, 1) не меняет знак, что вызывает некоторую надежду о том, что 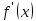 не меняет знак на всем отрезке (0, 1), но делать вывод об этом не совсем корректно с точки зрения математики. Однако анализ аналитического выражения
не меняет знак на всем отрезке (0, 1), но делать вывод об этом не совсем корректно с точки зрения математики. Однако анализ аналитического выражения 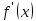 = –sin(x)–3 приводит к выводу, что
= –sin(x)–3 приводит к выводу, что 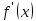 <= -2 при любых значениях x. А это значит, что
<= -2 при любых значениях x. А это значит, что 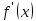 отрицательно на всем отрезке (0, 1), и уже из этого следует, что на отрезке (0, 1) функция f(x) монотонна и имеет один корень.
отрицательно на всем отрезке (0, 1), и уже из этого следует, что на отрезке (0, 1) функция f(x) монотонна и имеет один корень.Значения первой и второй производной
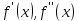 на отрезке (0, 1) из таблицы рис.1 будут использованы в методах Ньютона, хорд и итераций.
на отрезке (0, 1) из таблицы рис.1 будут использованы в методах Ньютона, хорд и итераций.Этап уточнения корня
Метод половинного деления
-
Исследование задания
-
Метод половинного деления сходится, если на выбранном отрезке отделен один корень. Так как на отрезке [0;1] функция меняет знак (
меняет знак (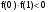 ) и монотонна (f′(x)<0), то условие сходимости выполняется.
) и монотонна (f′(x)<0), то условие сходимости выполняется. -
Выберем за начальное приближение середину отрезка
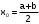 =0.5.
=0.5.-
Условие окончания процесса уточнения корня. Для оценки погрешности метода половинного деления справедливо условие
|bn – an|<ε , т.е. длина отрезка, полученного на n-ом шаге должна быть меньше заданной точности -
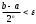
-
Результаты «ручного расчета» трех итераций
| 1 итерация 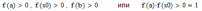 следовательно, 2 итерация 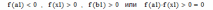 следовательно, 3 итерация 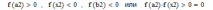 следовательно, и т.д. |