Графический способ решения систем двух уравнений первой степени с двумя неизвестными( учебник С.М. Никольский Алгебра 8 )Тип урока. урок изучения и первичного закрепления новых знаний, который является первым в системе уроков по теме « Графический способ решения систем уравненийЦель урока ознакомить учащихся с графическим способом решения систем и научить его применять при решении систем.Триединая дидактическая задача

• 
  Общеобразовательный аспект
  

1. 
   Продолжить формирование общеучебных умений и навыков:
   

• 
  умение планировать свою деятельность на уроке;
  
• 
  умение контролировать свою деятельность на уроке;
  
• 
  умение рассуждать, обобщать, делать выводы;
  
• 
  умение выполнять задания вычислительного и аналитического характера;
  
• 
  умение работать по образцу и в сходной ситуации при первичном закреплении.
  

Продолжить формирование специальных умений и навыков:

• 
  умение использовать теоретические сведения.
  

Развивающий аспект:

1. 
   продолжить развитие умения выделять главное, существенное, обобщать полученные факты:
   
2. 
   продолжить развитие логического мышления
   
3. 
   развивать познавательный интерес к предмету.
   

• 
  Воспитательный аспект:
  

Реализовать комплексный подход к воспитанию:

1. 
   воспитание воли, умение доводить начатое до конца, преодолевать трудности;
   
2. 
   формировать самооценку знаний, критическое отношение к себе, творческую активность, аккуратность, дисциплину, внимание
   

Методы и приёмы исследовательский и проблемный

Форма организации деятельности учащихся фронтальная, индивидуальная, самоанализ

Обоснование выбора формы проведения урока

Выбрана такая форма урока, которая смогла бы донести знания до учащихся как можно интереснее и доступнее, а это поиск и исследование. Поэтому, важной составляющей урока явился факт поиска общего в решении систем и графиком линейной функции и вывод, который сделают сами учащиеся.

---

Методы обучения на уроке

• 
  математические методы—моделирование, использование математического языка;
  
• 
  методы педагогики—методы организации и стимулирования учебной деятельности;
  
• 
  методы психологии—развитие мыслительных операций: анализ и синтез, сравнение и обобщение.
  

Организация учебной деятельности с учётом личностно- ориентированной технологии обучения

• 
  создание атмосферы взаимной заинтересованности в работе учащихся и учителя;
  
• 
  стимулирование учащихся к высказываниям, без боязни ошибиться, получить неправильный ответ;
  
• 
  оценка деятельности ученика не только по конечному результату( правильно-неправильно), но и по процессу его достижения;
  
• 
  создание педагогических ситуаций на уроке, позволяющих каждому ученику проявлять инициативу, самостоятельность;
  
• 
  создание ситуации выбора и успеха;
  
• 
  создание обстановки для естественного самовыражения ученика.
  

Организация учебной деятельности с учётом здоровьесберегающей технологии обучения

• 
  своевременная подготовка к уроку и его мобилизующее начало;
  

• 
  доброжелательная атмосфера, способствующая положительному и эмоциональному настрою
  
• 
  чёткая организация учебного труда;
  
• 
  смена видов деятельности учащихся
  

Оборудование: Учебник « Алгебра 8»под ред. С.М. Никольского; переносные доски с координатной плоскостьюСтруктура урока:

1. 
   организационный момент
   
2. 
   актуализация знаний
   
3. 
   получение новых знаний: наблюдая, обобщая
   
4. 
   применение полученных знаний
   
5. 
   домашнее задание
   
6. 
   итог урока
   

ХОД УРОКА1..Вступительное слово учителя Постановка цели урокаСегодня на уроке мы с вами познакомимся ещё с одним способом решения систем линейных уравнений с двумя неизвестными. Вы подниметесь ещё на одну ступеньку знаний, сделаете ещё одно маленькое открытие. Я вам в этом буду помогать. А для этого вы должны вспомнить те знания, которые вам помогут это открытие получить

---

2.Актуализация знаний

• 
  Устная работа ( на доске написано задание )
  

Выразить у через х 1. х + у =5 2. 2х – у = 0 3. у + 5х = 74. 3х + 4у = 0 5. х – 3у = 2 6. 2х – 2у = 4Ученики устно выполняют задание, и ответы записывают в тетрадь. Потом идёт проверка. Результат проверки ученики оценивают сами, На полях они выставляют себе столько баллов, сколько верно сделано заданий.

• 
  Работа в тетрадях и на доске
  

1. 
   Решить системы ( каждому ряду своя система, кто решает свою – решает следующую. Кто решит все три правильно—получает отметку) На доске три человека решают эти системы.
   

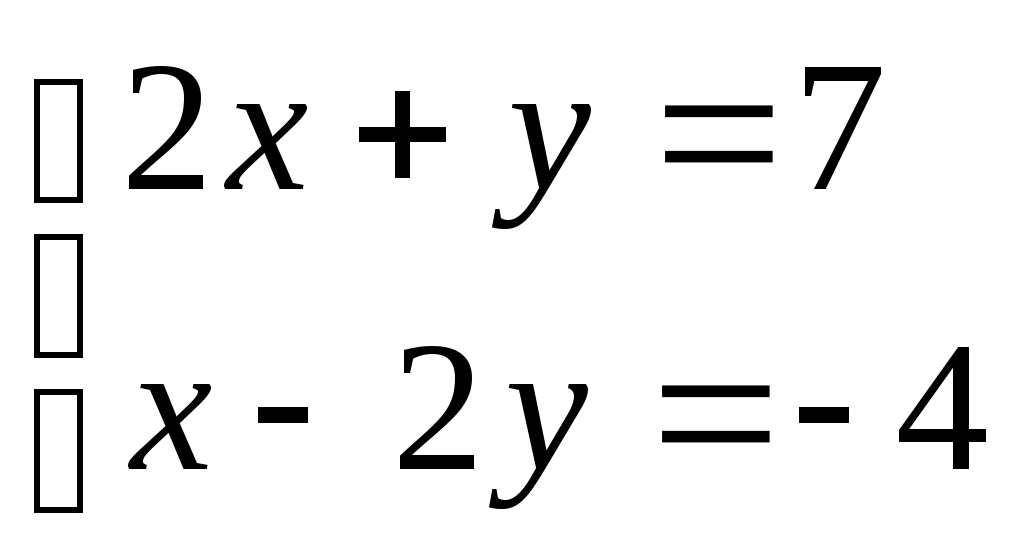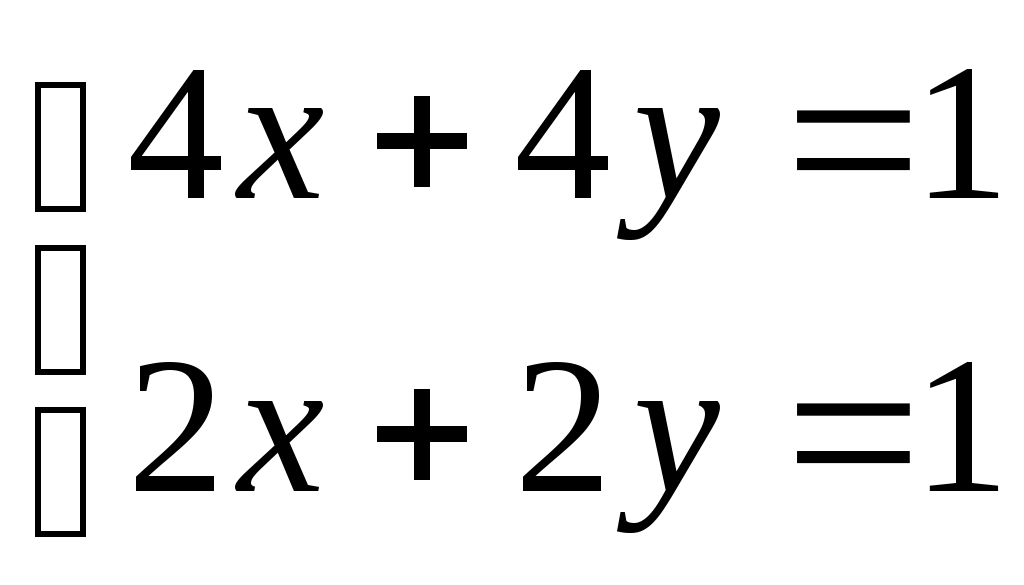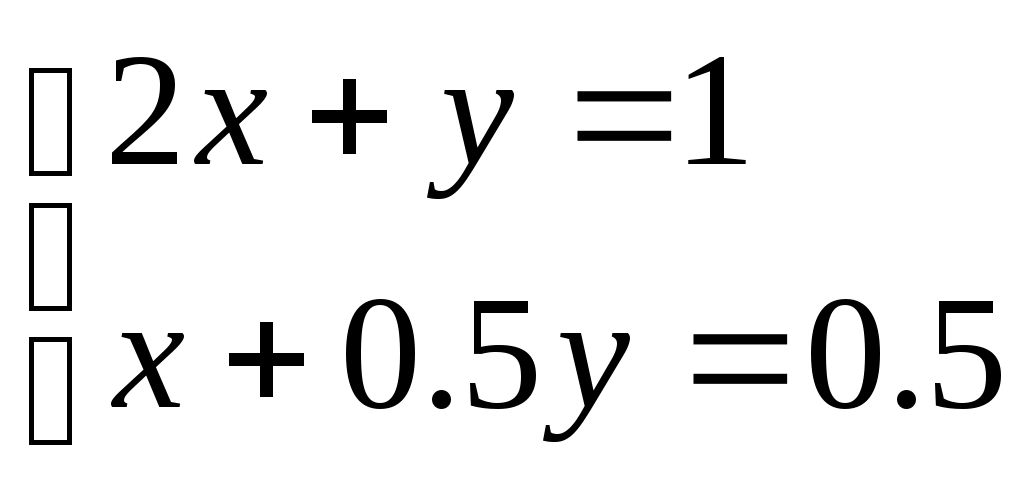
1. 2. 3. отв. ( 2;3) отв. нет решений отв. бесконечное мно-жество решенийВопросы отвечающим у доски:

1. 
   Что значит решить систему уравнений?
   
2. 
   Какие способы решения систем ты знаешь?
   
3. 
   Что является решением системы?
   
4. 
   Как проверить решение системы?
   

Решение систем проверяется. Отвечающим у доски выставляются отметки. Остальные --оценивают себя сами на полях. Опять количество баллов соответствует количеству правильно решённых системВопрос классу: Какие случаи могут встретиться при решении системы линейных уравнений с двумя неизвестными? Ершова Т.В. СОШ №4 им. В. Бурова г.Бежецк Тверская облОтвет учеников: одно решение, бесконечное множество решений, нет решений. Этот вывод заранее записан за доской.. 2.Построить графики функций ( каждому ряду своя функция, а четвёртая функция для тех, кто справится со своим заданием ) У доски графики строят 4 человека.1. у = 2х -1 2. у = - 3х 3. у = 3 4. 2х + у = 7Графики строят на переносных досках с координатной плоскостью. Выполнение заданий проверяется. Подробно разбирается 4 задание.

---

Вопросы отвечающим у доски:

1. 
   Что это за функции?
   
2. 
   Что является графиком линейной функции?
   
3. 
   Как строится график линейной функции?
   
4. 
   Какие графики будут параллельными прямыми и почему?
   
5. 
   К каждой функции задайте функцию, график которой будет ей параллелен.
   

Отвечающие у доски получают отметки, а все остальные на полях выставляют себе баллы по прежнему принципу.Вопрос классу: Как могу располагаться прямые на плоскости? Ответ учеников: пересекаться –одна общая точка; параллельные – нет общих точек; совпадать – бесконечное множество общих точек. Это вывод заранее записан за доской.3.Получение новых знанийРабота с классом. Обратить внимание учеников на то, что системы линейных уравнений состоят из линейных уравнений, а те в свою очередь являются линейными функциями. Возникает вопрос—а можно ли «связать» это вместе???Давайте ещё раз вернёмся к нашим выводам , сделанным на уроке. Открываются доски, на которых эти выводы записаныСистемыПрямые1.одно решение 1. пересекаются ( одна точка )2. нет решений 2. параллельные ( нет общих точек)3. бесконечное множество решений 3. совпадают ( бесконечное множество об- щих точек).Подвести учеников к выводу, что системы линейных уравнений с двумя переменными можно решать с помощью графиков. Это ещё один способ решения систем линейных уравнений.Проверим наши выводы на решённых системах в начале урока. Вернёмся к первой системе1. График первой функции у нас уже построен. Построим график второй функции в этой же координатной плоскости. У доски работает ученик. Графики пересеклись. Все находят координаты точки пересечения прямых и сравнивают их с ответом, полученным в начале урока. Они совпали. Попробуем составить алгоритм графического способа решения систем. Вместе с учениками составляется алгоритм. Открывается доска, на которой этот алгоритм был написанАлгоритм 1.1 уравнение: выразить

---

у через х и построить график | графики строить в одной2.2 уравнение: выразить у через х и построить график | координатной плоскости3.Сделать вывод:

• 
  если прямые пересеклись—есть решение и надо найти координаты точки пересечения—это и будет решением системы;
  
• 
  если прямые параллельны—то система не имеет решений;
  
• 
  если прямые совпали—то система имеет бесконечное множество решений
  

Остались ещё две системы. Под руководством учителя они решаются графически: ученик у доски, а все остальные в тетрадях. Ответы совпадают. Значит предположение и выводы были сделаны верно: системы можно решать графически.4 Применение полученных знанийЗадание из учебника № 822 (а)—решает один ученик у доски, объясняя свои действия.№822 (д) –решают все самостоятельно, а два ученика решают за доской для проверки и получают отметки, при их желании.5. Задание на дом п.9.1, записать в « шпаргалку» алгоритм решения систем графическим способом, № 822(б,г).6. Итог урока Вопрос классу. Что нового вы для себя узнали сегодня на уроке?Повторим алгоритм графического способа решения систем уравнений.Я могу вас сегодня только похвалить за активность и хорошую работу на уроке. Думаю, что проблем с домашним заданием у вас не будет. А теперь вы должны сами себя оценить. Сложите свои полученные баллы:Кто хочет поставить оценку в журнал вместе с тетрадью подойдёт к учителю. Кто не доволен своим результатом--- у вас всё впереди. Урок окончен. Спасибо всемРезультат деятельности учащихся:

• 
  понимание сути графического метода решения систем уравнений;
  
• 
  приобщение к процессу творчества, открытия для самого себя;
  
• 
  каждый ученик получил оценку своего труда на уроке и по желанию поставил её в журнал;
  
• 
  хорошее настроение.
  

---

Смотрите также файлы

• С. Москвичи "если бы вы попросили меня назвать наиболее значительное совершенно очевидной. С момента появления человеческого рода и до Возрождения горизонтом человека всегда было сообщество "мы" его группа или е.rtf

• Вопросы и задания Сформулируйте цели оценки персонала.docx

• Отчет по практической работе 1 По дисциплине.docx

• Протокол от план воспитательной работы 6 б класса мбоу сош 23.docx

• 10. Тепловой расчёт главного двигателя. План.docx