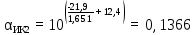
Кабельные потери вычисляем по формуле (20):





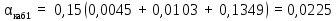
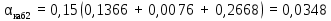
Суммировав полученные величины затухания, формула (21), вычислим величину полного затухания:





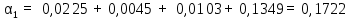
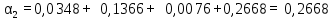
8. Расчет коэффициентов материальной, волноводной и хроматической дисперсии.

Коэффициент удельной материальной дисперсии [пс/(нм∙км)] определяется как:

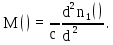(33)

Проведя вычисления в среде программирования Matlab получим следующий результат:





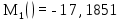
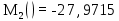
Коэффициент удельной волноводной дисперсии [пс/(нм∙км)] вычисляется по формуле:

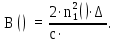(34)

Проведя вычисления в среде программирования Matlab получим следующий результат:





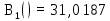
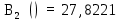
Коэффициент удельной хроматической дисперсии является суммой 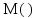и :

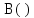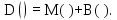(35)

Подставив значения, получим:





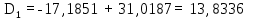
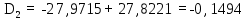
9. Определение длины волны нулевой дисперсии и вычисление наклона дисперсии в этой точке.

Наклон кривой хроматической дисперсии определяется в точке D = 0 по формуле:

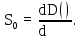(36)

Полученное значение:



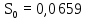
Длина волны нулевой дисперсии определяется при значении D = 0:



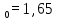
10. Построение графиков зависимости потерь от величины смещения на стыках разъемных соединений.

---

Зависимость потерь при радиальном смещении от величины смещения рассчитывается по формуле (20). Подставив значения получим график зависимости:



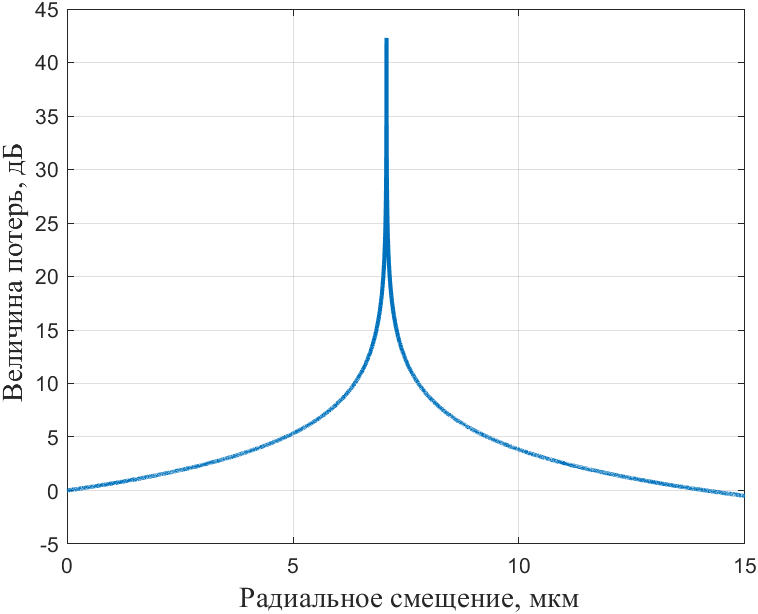
Рисунок 9 – График величины радиальных потерь

Потери при угловом смещении получим по формуле (17).



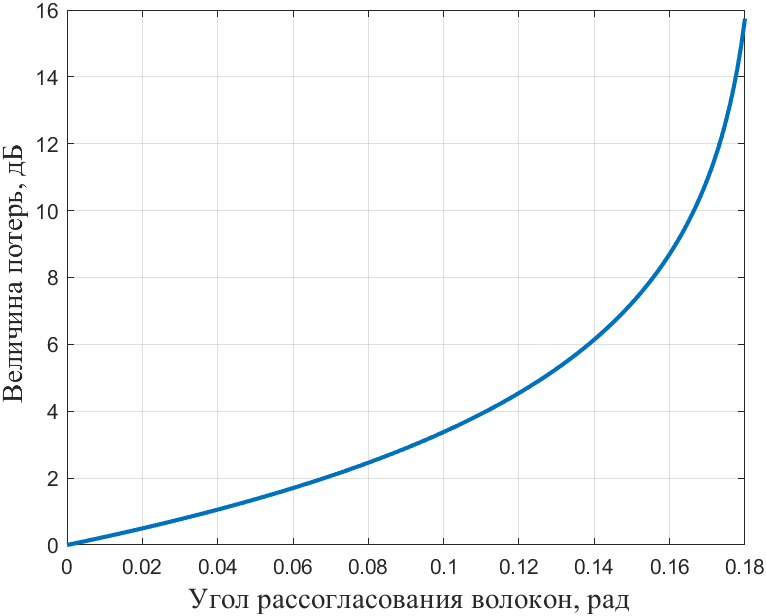
Рисунок 10 – График величины потерь при угловом смещении

Величину потерь при осевом смещении получим по формуле (26).



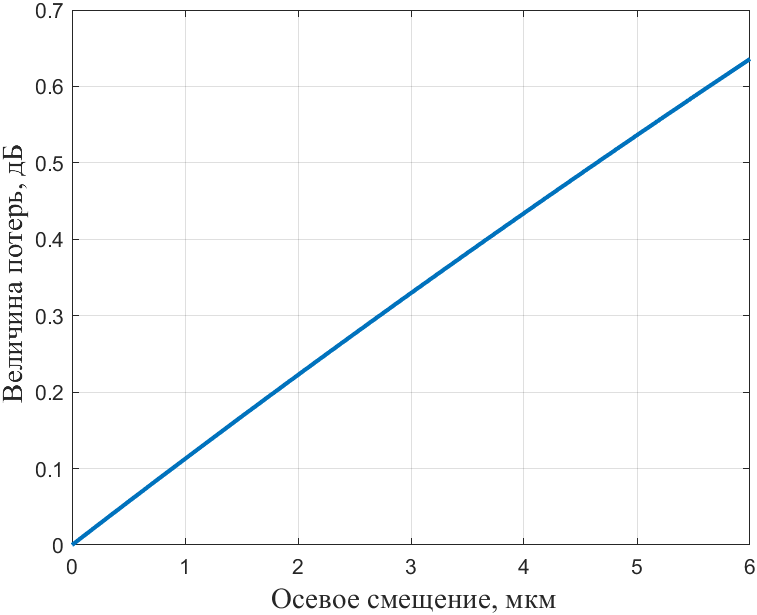
Рисунок 11 – График величины потерь при осевом смещении

11. Построение на одном графике зависимости коэффициентов дисперсии от длины волны.

Построим зависимости для коэффициентов: удельной материальной дисперсии по формуле (33), удельной волноводной дисперсии по формуле (34), удельной хроматической дисперсии по формуле (35).



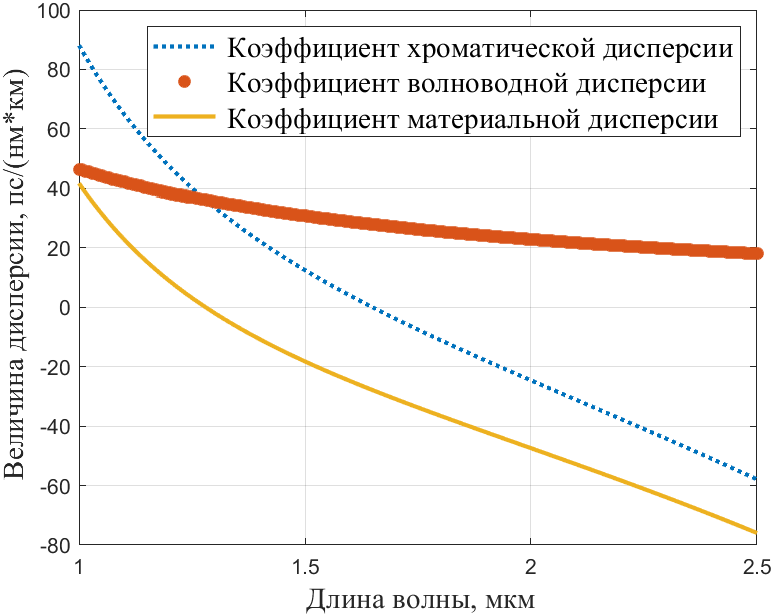
Рисунок 12 – График зависимости дисперсий от длины волны

Приложение

1.Многомодовый

clc;

clear;

lumbda1 = 0.846; % длина волны

lumbda2 = 1.29;

d = 50; % диаметр сердцевины волокна

D = 123;

delta = 0.02;

A1 = 0.6993390; % коэффициент Селмейера

A2 = 0.4111269;

A3 = 0.9035275;

my1 = 0.0617482; % коэффициент Селмейера

my2 = 0.1242404;

my3 = 9.896158;

% расчет числовой апертуры

n11 = sqrt(1+(lumbda1)^2*(A1/(lumbda1^2-my1^2)+A2/(lumbda1^2-my2^2)+A3/(lumbda1^2-my3^2)));

n21 = n11*(1-delta);

n12 = sqrt(1+(lumbda2)^2*(A1/(lumbda2^2-my1^2)+A2/(lumbda2^2-my2^2)+A3/(lumbda2^2-my3^2)));

n22 = n12*(1-delta);

NA1 = sqrt(n11^2-n21^2);

NA2 = sqrt(n12^2-n22^2);

%2 рассчет нормированный частоты

V1 = pi*d/lumbda1*NA1;

V2 = pi*d/lumbda2*NA2;

M1 = 0.5*V1^2; % число мод для ступенчатого ОВ

M2 = 0.5*V2^2;

M3 = 0.25*V1^2; % число мод для градиентного ОВ

M4 = 0.25*V2^2;

%3 межмодовая дисперсия

Lc1 = 6; % длина межмодовой связи для СП

Lc2 = 10; % длина межмодовой связи для ГП

L1 = 4; % длина линии передач для СП

L2 = 14; % длина линии передач для ГП

c = 3e5; % скорость света

TAY1 = (n11*delta/c)*L1; %для сппп

TAY2 = (n12*delta^2/(2*c))*L1; % для гппп

TAY3 = (n21*delta/c)*sqrt(L2*Lc1); %для сспп

TAY4 = (n22*delta^2/(2*c))*sqrt(L2*Lc2); % для гппп

%4 коэф широкополосности

dF1 = 0.44/TAY1; % для спп МГц\км

---

dF2 = 0.44/TAY2; % для гпп

dF3 = 0.44/TAY3; % для спп МГц\км

dF4 = 0.44/TAY4; % для гпп

%5 Коэффициент затухания

C = 0.6; % постоянный коэффициент

K1r = C*(n11^2-1)/lumbda1^4; % Рэлеевские потери

K1yf = 10^(2/lumbda1)/2154; % потери за счет поглощения в УФ области

K1ik = 10^(-21.9/lumbda1+12.4); % потери в ИК области

K1cab = 0.15*(K1r+K1yf+K1ik); % кабельные потери

K1 = K1r+K1yf+K1ik+K1cab; % затухание в ОВ дБ/км

K2r = C*(n12^2-1)/lumbda2^4;

K2yf = 10^(2/lumbda2)/2154;

K2ik = 10^(-21.9/lumbda2+12.4);

K2cab = 0.15*(K2r+K2yf+K2ik);

K2 = K2r+K2yf+K2ik+K2cab;

%6 графики

L = 0.5:0.001:1.9;

n1 = sqrt(1+(L).^2.*(A1./(L.^2-my1^2)+A2./(L.^2-my2^2)+A3./(L.^2-my3^2)));

Kr = C*(n1.^2-1)./L.^4; % Рэлеевские потери

Kyf = 10.^(2./L)/2154; % потери за счет поглощения в УФ области

Kik = 10.^(-21.9./L+12.4); % потери в ИК области

figure(1)

plot(L,Kr,'DisplayName','\fontname{Times New Roman}\fontsize{14} Рэлеевские потери','LineWidth', 2)

hold on

plot(L,Kyf,':','DisplayName','\fontname{Times New Roman}\fontsize{14} Потери в УФ области','LineWidth', 2)

plot(L,Kik,'--','DisplayName','\fontname{Times New Roman}\fontsize{14} Потери в ИК области','LineWidth', 2)

xlabel('\fontname{Times New Roman}\fontsize{14} Длина волны, мкм');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина потерь, дБ/км');

lgd=legend;

grid on

%7 затухание на макро и микро

N = 1:100;

R = 1e4:1e4:20e4;

Lmicr1 = N.*((32*(0.5)^2*d^4*n11^2)/(D^6*NA1^6));

Lmicr2 = N.*((32*(0.5)^2*d^4*n12^2)/(D^6*NA2^6));

Lmacr1 = - 10*log10(abs(1-d*n11^2/NA1^2./R)); % ДБ

Lmacr2 = - 10*log10(abs(1-d*n21^2/NA2^2./R)); % ДБ

figure(2)

plot(N,Lmicr1,'DisplayName','\fontname{Times New Roman}\fontsize{14} Микроизгибы для первой волны','LineWidth', 2)

hold on

plot(N,Lmicr2,':','DisplayName','\fontname{Times New Roman}\fontsize{14} Микроизгибы для второй волны','LineWidth', 2)

xlabel('\fontname{Times New Roman}\fontsize{14} Число микроизгибов');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина потерь, дБ');

lgd=legend;

grid on

figure(3)

plot(R/10e3,Lmacr1,'DisplayName','\fontname{Times New Roman}\fontsize{14} Макроизгибы для первой волны','LineWidth', 2)

hold on

plot(R/10e3,Lmacr2,'*','DisplayName','\fontname{Times New Roman}\fontsize{14} Макроизгибы для второй волны','LineWidth', 2)

xlabel('\fontname{Times New Roman}\fontsize{14} Радиус изгибов, см');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина потерь, дБ');

lgd=legend;

grid on

%8 потери на стыках

X1 = 0:0.01:50;

AAL = -10*log10(1-4*X1/pi/d);

X2 = 0:0.001:0.50;

AAS = -10*log10(1-2*X2/pi/asin(NA1));

X3 = 0:0.01:50;

n0 = 1;

AAO = -10*log10(1./(1+2*X3./d*tan(asin(NA1/n0))));

figure(4)

plot (X1,AAL,'LineWidth', 2), grid

xlabel('\fontname{Times New Roman}\fontsize{14} Радиальное смещение, мкм');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина потерь, дБ');

figure(5)

plot (X2,AAS,'LineWidth', 2), grid

xlabel('\fontname{Times New Roman}\fontsize{14} Угол рассогласования волокон, рад');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина потерь, дБ');

figure(6)

plot (X3,AAO,'LineWidth', 2), grid

xlabel('\fontname{Times New Roman}\fontsize{14} Осевое смещение, мкм');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина потерь, дБ');

2.Одномодовый

clc;

clear;

lumbda1 = 1.485; % длина волны

lumbda2 = 1.651;

d = 9; % диаметр сердцевины волокна

---

delta_d = 9 + 0.6; % погрешность изготовления

delta = 0.0033;

A1 = 0.6993390; % коэффициент Селмейера

A2 = 0.4111269;

A3 = 0.9035275;

my1 = 0.0617482; % коэффициент Селмейера

my2 = 0.1242404;

my3 = 9.896158;

% числовая апертура

n11 = sqrt(1+(lumbda1)^2*(A1/(lumbda1^2-my1^2)+A2/(lumbda1^2-my2^2)+A3/(lumbda1^2-my3^2)));

n21 = n11*(1-delta); % показатель преломления

n12 = sqrt(1+(lumbda2)^2*(A1/(lumbda2^2-my1^2)+A2/(lumbda2^2-my2^2)+A3/(lumbda2^2-my3^2)));

n22 = n12*(1-delta);

NA1 = sqrt(n11^2-n21^2); % числовая апертура

NA2 = sqrt(n12^2-n22^2);

% нормированная частота

V1 = pi*d/lumbda1*NA1;

V2 = pi*d/lumbda2*NA2;

% длина волны отсечки

Lo1 = pi*d*NA1/2.405;

Lo2 = pi*d*NA2/2.405;

% макс диаметр

Dmax1 = lumbda1*2.405/pi/NA1;

Dmax2 = lumbda2*2.405/pi/NA2;

% нормированная частота с погрешностью

V1err = pi*delta_d/lumbda1*NA1;

V2err = pi*delta_d/lumbda2*NA2;

% диаметр поля моды

w1 = d*(0.65+1.62*V1^(-3/2)+2.879*V1^(-6));

w2 = d*(0.65+1.62*V2^(-3/2)+2.879*V2^(-6));

% эффективная площадь модового поля

AA1 = pi*w1^2/4;

AA2 = pi*w2^2/4;

% Коэффициент затухания

C = 0.6;

K1r = C*(n11^2-1)/lumbda1^4; % Рэлеевские потери

K1yf = 10^(2/lumbda1)/2154; % потери за счет поглощения в УФ области

K1ik = 10^(-21.9/lumbda1+12.4); % потери в ИК области

K1cab = 0.15*(K1r+K1yf+K1ik); % кабельные потери

K1 = K1r+K1yf+K1ik+K1cab; % затухание в ОВ дБ/км

K2r = C*(n12^2-1)/lumbda2^4;

K2yf = 10^(2/lumbda2)/2154;

K2ik = 10^(-21.9/lumbda2+12.4);

K2cab = 0.15*(K2r+K2yf+K2ik);

K2 = K2r+K2yf+K2ik+K2cab;
% распределение поля по сечению

R = 0:0.01:4.0;

E1 = exp(-(R/w1).^2);

figure(1)

plot(R,E1,'LineWidth', 2), grid;

xlabel('\fontname{Times New Roman}\fontsize{14} Радиус поперечного сечения,мкм');

ylabel('\fontname{Times New Roman}\fontsize{14} Энергия поля, В');

xlim([0 4]);

E2 = exp(-(R/w2).^2);

figure(2)

plot(R,E2,'LineWidth', 2), grid;

xlabel('Радиус поперечного сечения,мкм')

ylabel('Энергия поля, В'), grid

xlim([0 4]);
% рассчет коэф. дисперсии

c = 3e5;

x1 = -(lumbda1/n11)*(A1*my1^2/(lumbda1^2-my1^2)^2+A2*my2^2/(lumbda1^2-my2^2)^2+A3*my3^2/(lumbda1^2-my3^2)^2);

M1 = lumbda1/n11/c*(A1*my1^2*(3*lumbda1^2+my1^2)/(lumbda1^2-my1^2)^3+A2*my2^2*(3*lumbda1^2+my2^2)/(lumbda1^2-my2^2)^3+A3*my3^2*(3*lumbda1^2+my3^2)/(lumbda1^2-my3^2)^3-x1^2)*1e9; % материальная дисперсия

B1 = 2*n11^2*delta/lumbda1/c*1e9; % удельная волноводная дисперсия

BM1 = M1 + B1;

x2 = -(lumbda2/n12)*(A1*my1^2/(lumbda2^2-my1^2)^2+A2*my2^2/(lumbda2^2-my2^2)^2+A3*my3^2/(lumbda2^2-my3^2)^2);

M2 = lumbda2/n12/c*(A1*my1^2*(3*lumbda2^2+my1^2)/(lumbda2^2-my1^2)^3+A2*my2^2*(3*lumbda2^2+my2^2)/(lumbda2^2-my2^2)^3+A3*my3^2*(3*lumbda2^2+my3^2)/(lumbda2^2-my3^2)^3-x2^2)*1e9;

B2 = 2*n12^2*delta/lumbda2/c*1e9;

BM2 = M2 + B2;
L11 = 1:0.005:2.5;

n111 = (sqrt(1+(L11).^2.*(A1./(L11.^2-my1^2)+A2./(L11.^2-my2^2)+A3./(L11.^2-my3^2))));

x11 = -(L11./n111).*(A1*my1^2./(L11.^2-my1^2).^2+A2*my2^2./(L11.^2-my2^2).^2+A3*my3^2./(L11.^2-my3^2).^2);

M11 = 1e9.*L11./n111./c.*(A1*my1.^2*(3*L11.^2+my1.^2)./(L11.^2-my1.^2).^3+A2*my2.^2*(3*L11.^2+my2.^2)./(L11.^2-my2.^2).^3+A3*my3.^2*(3*L11.^2+my3.^2)./(L11.^2-my3.^2).^3-x11.^2); % материальная дисперсия

B11 = 2*n111.^2*delta./L11/c*1e9; % удельная волноводная дисперсия

BM11 = M11 + B11;

figure(3)

plot(L11,BM11,':','DisplayName','\fontname{Times New Roman}\fontsize{14} Коэффициент хроматической дисперсии','LineWidth', 2)

---

hold on

plot(L11,B11,'*','DisplayName','\fontname{Times New Roman}\fontsize{14} Коэффициент волноводной дисперсии','LineWidth', 2)

plot(L11,M11,'DisplayName','\fontname{Times New Roman}\fontsize{14} Коэффициент материальной дисперсии','LineWidth', 2)

xlabel('\fontname{Times New Roman}\fontsize{14} Длина волны, мкм');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина дисперсии, пс/(нм*км)');

lgd=legend;

grid on
% потери на стыках

X1 = 0:0.001:15;

AAL = -10*log10(1-4*X1/pi/d);

X2 = 0:0.001:0.18;

AAS = -10*log10(1-2*X2/pi/asin(NA1));

X3 = 0:0.01:6;

n0 = 1;

AAO = -10*log10(1./(1+2*X3./d*tan(asin(NA1/n0))));

figure(4)

plot (X1,AAL,'LineWidth', 2), grid

xlabel('\fontname{Times New Roman}\fontsize{14} Радиальное смещение, мкм');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина потерь, дБ');

figure(5)

plot (X2,AAS,'LineWidth', 2), grid

xlabel('\fontname{Times New Roman}\fontsize{14} Угол рассогласования волокон, рад');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина потерь, дБ');

figure(6)

plot (X3,AAO,'LineWidth', 2), grid

xlabel('\fontname{Times New Roman}\fontsize{14} Осевое смещение, мкм');

ylabel('\fontname{Times New Roman}\fontsize{14} Величина потерь, дБ');

% наклон

Nul = 1.993;

syms L11;

F = 1e9.*L11./(sqrt(1+(L11).^2.*(A1./(L11.^2-my1^2)+A2./(L11.^2-my2^2)+A3./(L11.^2-my3^2))))./c.*(A1*my1.^2*(3*L11.^2+my1.^2)./(L11.^2-my1.^2).^3+A2*my2.^2*(3*L11.^2+my2.^2)./(L11.^2-my2.^2).^3+A3*my3.^2*(3*L11.^2+my3.^2)./(L11.^2-my3.^2).^3-(-(L11./(sqrt(1+(L11).^2.*(A1./(L11.^2-my1^2)+A2./(L11.^2-my2^2)+A3./(L11.^2-my3^2))))).*(A1*my1^2./(L11.^2-my1^2).^2+A2*my2^2./(L11.^2-my2^2).^2+A3*my3^2./(L11.^2-my3^2).^2)).^2)+2*(sqrt(1+(L11).^2.*(A1./(L11.^2-my1^2)+A2./(L11.^2-my2^2)+A3./(L11.^2-my3^2)))).^2*delta./L11/c*1e9;

dv = diff(F, 'L11', 1);

dy1 = subs(dv, 'L11', Nul);

df1 = double(dy1)/1e3;

---

Смотрите также файлы

• Сестринский уход при дисфункции кишечника.pdf

• В процессе организации своей работы какиелибо документы, неизбежно сталкивается с необходимостью их обработки.docx

• Вариант 1 Прочитай текст. Трусиха.doc

• Курсовая работа Конкурентоспособность России.docx

• Учебнометодические разработки для проведения лабораторных занятий по учебной дисциплине химия нефти и газа специальность направление подготовки.pdf