Файл: Курсовая работа по дисциплине Основы программирования систем управления (наименование дисциплины).docx
Добавлен: 04.12.2023
Просмотров: 40
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| |  | |
| МИНОБРНАУКИ РОССИИ | ||
| Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА – Российский технологический университет» РТУ МИРЭА | ||
| Институт искусственного интеллекта | ||
| (наименование института, филиала) | ||
| Кафедра проблем управления | ||
| (наименование кафедры) | ||
| КУРСОВАЯ РАБОТА |
по дисциплине «Основы программирования систем управления»
(наименование дисциплины)
Тема курсовой работы: «Решение нелинейного уравнения методом половинного деления»
Студент группы КВБО-02-21 Редько Артемий Вадимович _____________________
(учебная группа, фамилия, имя, отчество студента) (подпись студента)
Руководитель курсовой работы: Старший преподаватель, Петухов Алексей Михайлович
_______________________
(подпись руководителя)
Работа представлена к защите «___» _______________ 2022 г.
Допущен к защите «___» _______________ 2022 г.
Москва 2022 г.
| | | |
| МИНОБРНАУКИ РОССИИ | ||
| Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА – Российский технологический университет» РТУ МИРЭА | ||
| Институт искусственного интеллекта | ||
| (наименование института, филиала) | ||
| Кафедра проблем управления | ||
| (наименование кафедры) | ||
| | Утверждаю |
| | Заведующий кафедрой ПУ _________________ /Романов М.П./ подпись ФИО |
| | «___» ____________ 2022 г. |
| ЗАДАНИЕ | |
| на выполнение курсовой работы по дисциплине «Основы программирования систем управления» | |
Студент Редько Артемий Вадимович Группа КВБО-02-21
Тема «Решение нелинейного уравнения методом половинного деления»
Исходные данные:
Срок представления к защите курсовой работы: до «___» ___________ 2022 г. |
| |
| Задание на выполнение курсовой работы выдал ____________________ (Петухов А.М.) подпись руководителя Ф.И.О. руководителя |
«___» _______________ 2022 г.
Задание на курсовую работу получил __________________ (Редько А.В.)
подпись обучающегося Ф.И.О. исполнителя
Содержание
Введение
Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня. В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума. В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений. В простейшем случае у нас имеется функция ƒ, заданная на отрезке (a, b) и принимающая определенные значения. Каждому значению
x из этого отрезка мы можем сопоставить число ƒ(x), это и есть функциональная зависимость, ключевое понятие математики. Нам нужно найти такое значение x, при котором ƒ(x) = 0, такие x называются корнями функции ƒ. Визуально нам нужно определить точку пересечения графика функции ƒ(x) с осью абсцисс.
Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений. В данной работе будет представлено решение нелинейного уравнения
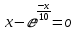. Основная часть
-
Описание метода
Простейшим методом нахождения корней уравнения ƒ(x) = 0 является метод деления пополам или дихотомия. Дихотоми́я (греч. διχοτομία: δῐχῆ, «надвое» + τομή, «деление») — раздвоенность, последовательное деление на две части, более связанные внутри, чем между собой. Способ логического деления класса на подклассы, который состоит в том, что делимое понятие полностью делится на два взаимоисключающих понятия. Дихотомическое деление в математике, философии, логике и лингвистике является способом образования подразделов одного понятия или термина и служит для образования классификации элементов. Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.
Алгоритм состоит в следующем: предположим, мы нашли две точки a и b, такие что ƒ(a) и ƒ(b) имеют разные знаки. Тогда между этими точками находится хотя бы один корень функции ƒ. Поделим отрезок [a, b] пополам и введем среднюю точку
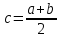. Тогда либо ƒ(a)ƒ(c) <0, либо ƒ(c)ƒ(b) <0.Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее до достижения требуемой точности. Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его. Описанный алгоритм применим для любой непрерывной функции.
Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое: чем больше сделано итераций, тем точнее определен корень.
-
Преимущества и недостатки метода
Дихотомическое деление привлекательно своей простотой. Действительно, при дихотомии мы всегда имеем дело лишь с двумя классами, которые исчерпывают объём делимого понятия. Таким образом, дихотомическое деление всегда соразмерно;
члены деления дополняют друг друга, так как каждый объект делимого множества попадает только в один из классов а или не а; деление проводится по одному основанию — наличие или отсутствие некоторого признака. Обозначив делимое понятие буквой а и выделив в его объёме некоторый вид, скажем, b, можно разделить объём а на две части — b и не b.
Дихотомическое деление имеет недостаток: при делении объёма понятия на два понятия каждый раз остаётся крайне неопределённой та его часть, к которой относится частица «не». Если разделить учёных на историков и не историков, то вторая группа оказывается весьма неясной. Кроме того, если в начале дихотомического деления обычно довольно легко установить наличие противоречащего понятия, то по мере удаления от первой пары понятий найти его становится всё труднее.
Вышеописанные преимущества и недостатки описываются в общем случае. Касаемо поиска корней нелинейного уравнения, мы имеем следующее: к достоинствам метода деления пополам следует отнести его высокую надежность и простоту; недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.
-
Применение
Дихотомия обычно используется как вспомогательный приём при установлении классификации.
Она известна также благодаря достаточно широко используемому методу поиска, так называемому методу дихотомии. Он применяется для нахождения значений действительно-значной функции, определяемых по какому-либо критерию (это может быть сравнение на минимум, максимум или конкретное число).
Рассмотрим метод на конкретном примере: Вася задумал целое число от одного до десяти включительно. Он честно отвечает на вопросы Пети «да» или «нет». Какое минимальное число вопросов потребуется Пете, чтобы гарантированно отгадать задуманное число?
Под фразой «гарантированно отгадать» следует понимать, что какое бы число из диапазона [1…10]{\displaystyle [1..10]} ни было загадано, задавая вопросы в соответствии с некоторым правилом, Пете заведомо хватит{\displaystyle M} M вопросов, где M {\displaystyle M} — искомый минимум. Строго говоря, предлагается не только ответить на вопрос задачи, но и составить
алгоритм отгадывания задуманного числа за минимальное число вопросов.
Отвлечёмся и вспомним более простую задачу. Для этого вспомним, что такое один бит информации. Бит — это количество информации, уменьшающее степень неопределённости в два раза.
Классический пример — представим себе, что Вася не готовился к контрольной работе по математике, и может получить любую из оценок от двойки до пятерки. И, по окончании работы, на вопрос «Как контрольная?» следует ответ: «Четыре!». Сколько бит информации сообщил Вася?
Для того, чтобы ответить на этот вопрос, разобьём наш вопрос «Как контрольная?» на этапы, причём таким образом, чтобы на каждом этапе неопределённость уменьшалась ровно в два раза. С точки зрения нормального человека это довольно необычный способ узнать ответ на вопрос, но, тем не менее, приступим.
Первым этапом может быть, например, вопрос: «Оценка выше тройки?» Всего различных оценок четыре, этот вопрос разделяет их на две группы — «больше трёх» и «меньше либо равно трём». Очень важно, что эти группы одинаковы по количеству элементов — в каждой ровно по две возможных оценки. В первой группе находятся «отлично» и «хорошо», во второй — «удовлетворительно» и «неудовлетворительно». Теперь нам предстоит определить одну оставшуюся оценку из двух, то есть уменьшить неопределённость ещё в два раза и получить ещё один бит информации. Отсюда следует, что искомое число бит в ответе Васи «Четвёрка!» равно двум — первый бит из четырёх возможных вариантов выбирает два, второй — выбирает из двух один.
Необходимо отметить, что разбиение потенциальных оценок на «группы» — исключительно дело вкуса, нужно лишь чтобы эти группы состояли из одинакового числа элементов. Вопрос первого этапа мог бы звучать, например, так: «Твоя оценка — двойка или пятерка?»
Очевидно, что в данном случае в ответ закрадываются степени двойки. Для того, чтобы передать один из двух возможных вариантов, требуется один бит. Два бита могут передать один из 2×2=4 вариантов. Три бита — один из 2×2×2=8 вариантов. С помощью n бит можно передать один из
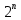вариантов.В какую минимальную степень n необходимо возвести двойку, чтобы она стала больше десяти? В четвёртую,
