Файл: Курсовая работа по дисциплине Основы программирования систем управления (наименование дисциплины).docx
Добавлен: 04.12.2023
Просмотров: 41
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Из предыдущего абзаца следует, что четырёх вопросов будет достаточно для отгадывания. Первая часть задачи решена.
А как следует задавать вопросы, чтобы уложиться в дозволенные четыре вопроса? Уж точно не отгадывать число по порядку, начиная с единицы — это ведёт в худшем случае к девяти вопросам. Общее правило одно — нужно каждым вопросом уменьшать неопределённость в два раза. Если число вариантов не является степенью двойки, то в некоторых вопросах количество вариантов в «половинах» может различаться, но не более, чем на единицу. Итак, перед первым вопросом мы имеем десять различных вариантов. Десять пополам — пять. Спросим: «Задуманное число больше пяти?» Теперь самое главное не ошибиться нигде на единицу: не сказать, не подумав «больше» вместо «больше либо равно» и наоборот.
После ответа на первый вопрос вариантов осталось пять. Нам нужно разбить их на группы, состоящие из двух и трёх элементов. Например, если выяснилось, что задуманное число больше пяти, корректно будет спросить: «Верно ли, что задуманное число больше либо равно восьми?»
Третьим вопросом мы снижаем число вариантов с двух до одного либо с трёх до двух. Если после второго вопроса осталось всего два варианта (например, на вопрос: «Число больше либо равно восьми?» последовал отрицательный ответ), то потребуется всего три, а не четыре вопроса. В любом случае, последним вопросом мы выбираем между двумя оставшимися числами и узнаём ответ.
Рассмотрим более актуальную задачу: поиск элемента в массиве. Пусть мы имеем упорядоченный по неубыванию массив M из, скажем,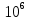
элементов. Нам необходимо найти индекс i-го элемента, значение которого равно x:
M[i] = x, i = ?
Как решить эту задачу максимально быстро, то есть за возможно меньшее число обращений к массиву? Ясно, что проверять все элементы массива начиная с первого — не лучшая идея. Необходимо придумать способ, который подстраивал бы следующую «попытку» на основании предыдущих. Не подойдет ли здесь метод дихотомии?
Вспомним поиск в словаре незнакомого слова — для простоты положим, что мы точно знаем написание. Но перебор всех слов с начала словаря не является оптимальным вариантом поиска. Если это словарь русского языка, в котором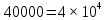
слов, и наша «скорость сканирования» составляет одно слово в секунду (не считая переворачивания страниц), то процесс пролистывания словаря займёт
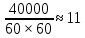часов.
Вероятнее всего, вначале мы найдём первую букву искомого слова. Это обычно несложно сделать, учитывая то, что первые буквы в словаре обычно помечены специальным образом. Затем, когда мы знаем, с какой по какую страницу искать искомое слово, логично искать вторую букву (строго говоря, человеческий мозг использует несколько другой механизм поиска, который грубо можно аппроксимировать градиентным методом оптимизации, тем не менее, пример со словарем достаточно показателен), за ней третью и так далее. В итоге либо искомое слово будет найдено, либо найдутся два слова, между которыми оно должно быть, но его там нет.
Похожим образом мы ищем элемент в упорядоченном массиве. Пусть для простоты мы заранее проверили, что M[1] < x и M[N] > x. Обратим внимание на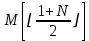
. Если мы «промахнулись» мимо искомого элемента (что более чем вероятно для первой итерации) — не беда, мы теперь точно знаем в какой половине массива искать. Метод дихотомии преуспевает в решении и этой задачи.
Маленькая хитрость — при поиске элемента в массиве, и вообще, если подбираемый параметр — целое число, область поиска можно запоминать не как отрезок [a; b] или интервал (a; b), а как полуинтервал [a; b). В большинстве случаев это упрощает переход от итерации к следующей, и сильно экономит время, затраченное впоследствии на отладку программы.
Нельзя не упомянуть и метод сортировки массива, алгоритм которого несколько напоминает алгоритм поиска корня нелинейного уравнения при использовании метода половинного деления. Эта сортировка имеет название «Быстрая сортировка». Алгоритм состоит из трёх шагов. Сначала из массива нужно выбрать один элемент — его обычно называют опорным. Затем другие элементы в массиве перераспределяют так, чтобы элементы меньше опорного оказались до него, а большие или равные — после. А дальше рекурсивно применяют первые два шага к подмассивам справа и слева от опорного значения. Следует отметить, что быстрая сортировка имеет асимптотическую сложность O(N×log N), и это лучшая возможная асимптотика времени сортировки.
Быструю сортировку изобрели в 1960 году для машинного перевода: тогда словари хранились на магнитных лентах, а сортировка слов обрабатываемого текста позволяла получить переводы за один прогон ленты, без перемотки назад.
Часто бывает непросто увидеть метод дихотомии в хорошей задаче по информатике. В завершение обоснования актуальности приведу пример — задача «Провода́» с полуфинала чемпионата мира по программированию ACM, проходившему в Санкт-Петербурге в октябре 2002 года.
На складе имеется N проводов целочисленной длины. Необходимо из них получить K кусков провода одинаковой и как можно большей длины L. Провода нельзя спаивать.
В первой строчке указаны числа N и K, 1 ≤ N, K ≤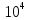
. Далее разделённые пробельными символами перечислены N натуральных чисел — длины имеющихся проводов. Они не превосходят 
.
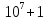Выведите целое максимальное число L — такое, что можно из имеющихся проводов получить K кусочков длины L.
Рассуждения о способах разрезания проводов, конечно, могут привести к решению, но гораздо более простой путь — дихотомия по длине провода. Функция общего числа проводов от проверяемой длины легко вычисляется, она, очевидно, является монотонной, и искать решение можно, например, на интервале от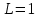
до 
.
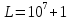Задача сводится к классической дискретной дихотомии, и её решение оказывается на удивление простым.
Ход работы
Перед непосредственным выполнением работы, была составлена блок – схема (Рис.1), описывающая работу программы, а также изучена вышеописанная теоретическая часть работы метода половинного деления. Наличие блок – схемы, в общем случае, облегчает написание кода, за счет обеспечивания легкой «читаемости» алгоритма.
Рассмотрим схему: на вход подается три числа; a, b – начало и конец заданного отрезка соответственно; е – допустимая погрешность (она же заданная точность). Затем вычисляется произведение значений функции от чисел a и b. Если произведение меньше нуля, то условие сходимости выполнено, то есть на концах отрезка функция принимает разные по знаку значения, значит есть точка x в этом отрезке такая, что ƒ(x) = 0, другими словами, x – корень нашего уравнения. Тогда мы можем инициализировать счетчик итераций нулем и объявить цикл. В цикле мы ищем серидину нашего исходного отрезка (точка
x), количество итераций увеличиваем на единицу. Если значение функции в середине отрезка меньше заданной точности, то проверяем условие сходимости: если на концах отрезка [a; x] функция имеет разные знаки, то за начало отрезка берем a, а за конец – x. В противном случае началом отрезка становится x, а концом – b. Описанные операции будут выполняться до тех пор, пока абсолютное значение функции в середине отрезка не станет меньше допустимой погрешности. Как только мы выходим из цикла – выводим значение корня уравнения и количество итераций, x и N соответственно.
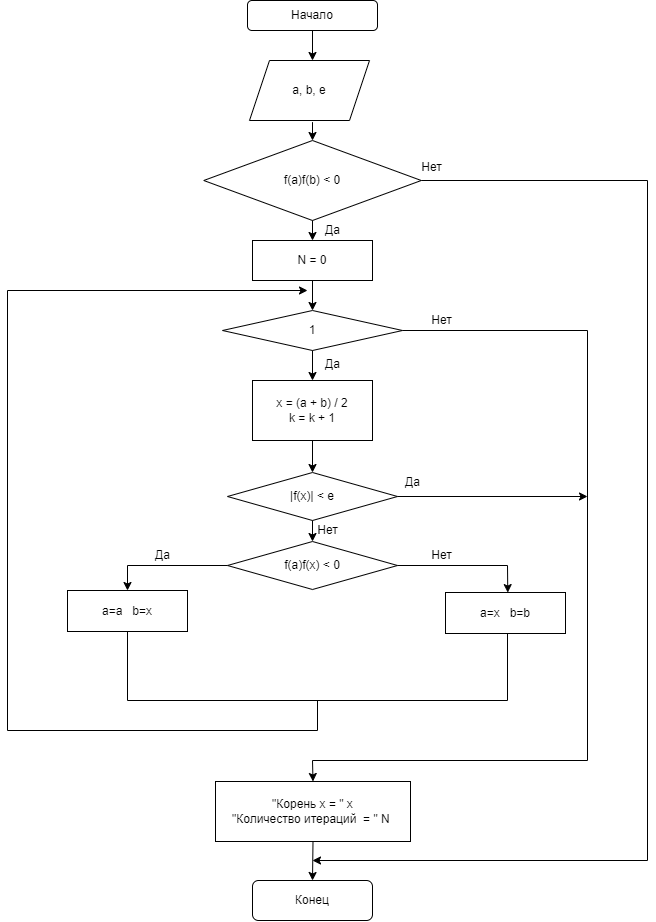
Рис.1. Алгоритм работы метода половинного деления.
Листинг кода представлен в приложении А. Для начала подключим библиотеку «iostream». Iostream объявляет объекты, управляющие чтением из стандартных потоков и записью в них. Это часто является единственным заголовком, который требуется выполнить в программе C++ для ввода и вывода. Следующим шагом объявим пространство имён std, которое открывает пространство имён библиотеки iostream. После чего описываем функцию с нашим уравнением
. В качестве возвращаемого значения указываем значение функции ƒ. Следующая функция под названием «solve» реализует метод половинного деления, алгоритм которого был проиллюстрирован в блок – схеме (Рис.1) и описан в первой части хода работы. Setlocale был добавлен для подключения русского языка, иначе говоря – более удобного считывания выходных данных. Стоит отметить, что x был инициализирован единицей (double x = 1) , так как, по условию задачи,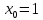 
– начальное приближение. Также, в конце каждой итерации цикла while выводились значения x и n для наглядности работы алгоритма и обработки результатов. В главной функции main инициализируются и выводятся на экран исходные данные. После чего происходит вызов функции «solve». Так как имя функции является её указателем, а результатом работы является значение искомого x, то при вызове функции по указателю в главную функцию передается результат работы программы.
Рассмотрим результаты работы программы (Рис. 2):
Р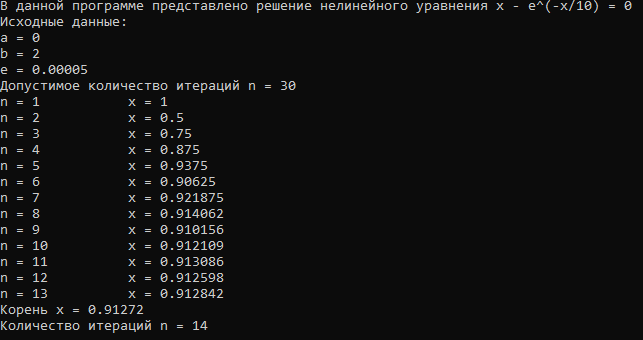
ис. 2. Выходные данные.
Условия задачи соблюдены: сначала были напечатаны исходные данные (их вывод был реализован в главной функции), затем результат вычислений. Видно, что при каждой итерации значение следующего x все меньше отличается от предыдущего. Точность вычислений можно увеличить уменьшением значения заданной точности, но при этом возрастет количество итераций.
Заключение
В результате выполнения курсовой работы по дисциплине «Основы программирования систем управления» было решено нелинейное уравнение . Программа написана в среде разработки Microsoft Visual Studio Enterprise 2019 на языке C++.
В руках опытного программиста метод дихотомии представляет собой мощный инструмент для поиска точных ответов в случае дискретных, и приближённых, но весьма точных, — в случае непрерывных задач. Является наиболее простым для решения уравнений в численных методах.
Список литературы
приложение А
Листинг 1
#include
#include
using namespace std;
double f(double x)
{
double f;
f = x - exp(-x / 10);
return f;
}
void solve(double a, double b, double e)
{
setlocale(LC_ALL, "rus");
double x = 1;
int n;
if (f(a) * f(b) < 0)
{
n = 0;
while (1)
{
x = (a + b) / 2.0;
n++;
if (fabs(f(x)) < e) break;
if (f(a) * f(x) < 0)
{
a = a; b = x;
}
else
{
a = x; b = b;
}
cout << "n = " << n << "\t\t";
cout << "x = " << x << endl;
}
cout << "Корень x = " << x << endl;
cout << "Количество итераций n = " << n << endl;
}
}
int main()
{
double a, b, e, x;
int n;
setlocale(LC_ALL, "rus");
a = 0.0; b = 2.0; e = 0.00005;
cout << "В данной программе представлено решение нелинейного уравнения x - e^(-x/10) = 0\n";
cout << "Исходные данные:\n";
cout << "a = " << a << endl;
cout << "b = " << b << endl;
cout << "e = 0.00005" << endl;
cout << "Допустимое количество итераций n = 30" << endl;
solve(a, b, e);
}
А как следует задавать вопросы, чтобы уложиться в дозволенные четыре вопроса? Уж точно не отгадывать число по порядку, начиная с единицы — это ведёт в худшем случае к девяти вопросам. Общее правило одно — нужно каждым вопросом уменьшать неопределённость в два раза. Если число вариантов не является степенью двойки, то в некоторых вопросах количество вариантов в «половинах» может различаться, но не более, чем на единицу. Итак, перед первым вопросом мы имеем десять различных вариантов. Десять пополам — пять. Спросим: «Задуманное число больше пяти?» Теперь самое главное не ошибиться нигде на единицу: не сказать, не подумав «больше» вместо «больше либо равно» и наоборот.
После ответа на первый вопрос вариантов осталось пять. Нам нужно разбить их на группы, состоящие из двух и трёх элементов. Например, если выяснилось, что задуманное число больше пяти, корректно будет спросить: «Верно ли, что задуманное число больше либо равно восьми?»
Третьим вопросом мы снижаем число вариантов с двух до одного либо с трёх до двух. Если после второго вопроса осталось всего два варианта (например, на вопрос: «Число больше либо равно восьми?» последовал отрицательный ответ), то потребуется всего три, а не четыре вопроса. В любом случае, последним вопросом мы выбираем между двумя оставшимися числами и узнаём ответ.
Рассмотрим более актуальную задачу: поиск элемента в массиве. Пусть мы имеем упорядоченный по неубыванию массив M из, скажем,
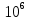элементов. Нам необходимо найти индекс i-го элемента, значение которого равно x:M[i] = x, i = ?
Как решить эту задачу максимально быстро, то есть за возможно меньшее число обращений к массиву? Ясно, что проверять все элементы массива начиная с первого — не лучшая идея. Необходимо придумать способ, который подстраивал бы следующую «попытку» на основании предыдущих. Не подойдет ли здесь метод дихотомии?
Вспомним поиск в словаре незнакомого слова — для простоты положим, что мы точно знаем написание. Но перебор всех слов с начала словаря не является оптимальным вариантом поиска. Если это словарь русского языка, в котором
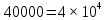слов, и наша «скорость сканирования» составляет одно слово в секунду (не считая переворачивания страниц), то процесс пролистывания словаря займёт
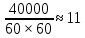часов.Вероятнее всего, вначале мы найдём первую букву искомого слова. Это обычно несложно сделать, учитывая то, что первые буквы в словаре обычно помечены специальным образом. Затем, когда мы знаем, с какой по какую страницу искать искомое слово, логично искать вторую букву (строго говоря, человеческий мозг использует несколько другой механизм поиска, который грубо можно аппроксимировать градиентным методом оптимизации, тем не менее, пример со словарем достаточно показателен), за ней третью и так далее. В итоге либо искомое слово будет найдено, либо найдутся два слова, между которыми оно должно быть, но его там нет.
Похожим образом мы ищем элемент в упорядоченном массиве. Пусть для простоты мы заранее проверили, что M[1] < x и M[N] > x. Обратим внимание на
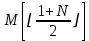. Если мы «промахнулись» мимо искомого элемента (что более чем вероятно для первой итерации) — не беда, мы теперь точно знаем в какой половине массива искать. Метод дихотомии преуспевает в решении и этой задачи.Маленькая хитрость — при поиске элемента в массиве, и вообще, если подбираемый параметр — целое число, область поиска можно запоминать не как отрезок [a; b] или интервал (a; b), а как полуинтервал [a; b). В большинстве случаев это упрощает переход от итерации к следующей, и сильно экономит время, затраченное впоследствии на отладку программы.
Нельзя не упомянуть и метод сортировки массива, алгоритм которого несколько напоминает алгоритм поиска корня нелинейного уравнения при использовании метода половинного деления. Эта сортировка имеет название «Быстрая сортировка». Алгоритм состоит из трёх шагов. Сначала из массива нужно выбрать один элемент — его обычно называют опорным. Затем другие элементы в массиве перераспределяют так, чтобы элементы меньше опорного оказались до него, а большие или равные — после. А дальше рекурсивно применяют первые два шага к подмассивам справа и слева от опорного значения. Следует отметить, что быстрая сортировка имеет асимптотическую сложность O(N×log N), и это лучшая возможная асимптотика времени сортировки.
Быструю сортировку изобрели в 1960 году для машинного перевода: тогда словари хранились на магнитных лентах, а сортировка слов обрабатываемого текста позволяла получить переводы за один прогон ленты, без перемотки назад.
Часто бывает непросто увидеть метод дихотомии в хорошей задаче по информатике. В завершение обоснования актуальности приведу пример — задача «Провода́» с полуфинала чемпионата мира по программированию ACM, проходившему в Санкт-Петербурге в октябре 2002 года.
На складе имеется N проводов целочисленной длины. Необходимо из них получить K кусков провода одинаковой и как можно большей длины L. Провода нельзя спаивать.
В первой строчке указаны числа N и K, 1 ≤ N, K ≤
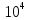. Далее разделённые пробельными символами перечислены N натуральных чисел — длины имеющихся проводов. Они не превосходят 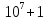.Выведите целое максимальное число L — такое, что можно из имеющихся проводов получить K кусочков длины L.
Рассуждения о способах разрезания проводов, конечно, могут привести к решению, но гораздо более простой путь — дихотомия по длине провода. Функция общего числа проводов от проверяемой длины легко вычисляется, она, очевидно, является монотонной, и искать решение можно, например, на интервале от
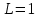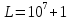до .Задача сводится к классической дискретной дихотомии, и её решение оказывается на удивление простым.
Ход работы
-
Подготовка к выполнению
Перед непосредственным выполнением работы, была составлена блок – схема (Рис.1), описывающая работу программы, а также изучена вышеописанная теоретическая часть работы метода половинного деления. Наличие блок – схемы, в общем случае, облегчает написание кода, за счет обеспечивания легкой «читаемости» алгоритма.
Рассмотрим схему: на вход подается три числа; a, b – начало и конец заданного отрезка соответственно; е – допустимая погрешность (она же заданная точность). Затем вычисляется произведение значений функции от чисел a и b. Если произведение меньше нуля, то условие сходимости выполнено, то есть на концах отрезка функция принимает разные по знаку значения, значит есть точка x в этом отрезке такая, что ƒ(x) = 0, другими словами, x – корень нашего уравнения. Тогда мы можем инициализировать счетчик итераций нулем и объявить цикл. В цикле мы ищем серидину нашего исходного отрезка (точка
x), количество итераций увеличиваем на единицу. Если значение функции в середине отрезка меньше заданной точности, то проверяем условие сходимости: если на концах отрезка [a; x] функция имеет разные знаки, то за начало отрезка берем a, а за конец – x. В противном случае началом отрезка становится x, а концом – b. Описанные операции будут выполняться до тех пор, пока абсолютное значение функции в середине отрезка не станет меньше допустимой погрешности. Как только мы выходим из цикла – выводим значение корня уравнения и количество итераций, x и N соответственно.
Рис.1. Алгоритм работы метода половинного деления.
-
Реализация кода
Листинг кода представлен в приложении А. Для начала подключим библиотеку «iostream». Iostream объявляет объекты, управляющие чтением из стандартных потоков и записью в них. Это часто является единственным заголовком, который требуется выполнить в программе C++ для ввода и вывода. Следующим шагом объявим пространство имён std, которое открывает пространство имён библиотеки iostream. После чего описываем функцию с нашим уравнением
. В качестве возвращаемого значения указываем значение функции ƒ. Следующая функция под названием «solve» реализует метод половинного деления, алгоритм которого был проиллюстрирован в блок – схеме (Рис.1) и описан в первой части хода работы. Setlocale был добавлен для подключения русского языка, иначе говоря – более удобного считывания выходных данных. Стоит отметить, что x был инициализирован единицей (double x = 1) , так как, по условию задачи, 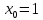– начальное приближение. Также, в конце каждой итерации цикла while выводились значения x и n для наглядности работы алгоритма и обработки результатов. В главной функции main инициализируются и выводятся на экран исходные данные. После чего происходит вызов функции «solve». Так как имя функции является её указателем, а результатом работы является значение искомого x, то при вызове функции по указателю в главную функцию передается результат работы программы. -
Обработка результатов
Рассмотрим результаты работы программы (Рис. 2):
Р
ис. 2. Выходные данные.
Условия задачи соблюдены: сначала были напечатаны исходные данные (их вывод был реализован в главной функции), затем результат вычислений. Видно, что при каждой итерации значение следующего x все меньше отличается от предыдущего. Точность вычислений можно увеличить уменьшением значения заданной точности, но при этом возрастет количество итераций.
Заключение
В результате выполнения курсовой работы по дисциплине «Основы программирования систем управления» было решено нелинейное уравнение
. Программа написана в среде разработки Microsoft Visual Studio Enterprise 2019 на языке C++.В руках опытного программиста метод дихотомии представляет собой мощный инструмент для поиска точных ответов в случае дискретных, и приближённых, но весьма точных, — в случае непрерывных задач. Является наиболее простым для решения уравнений в численных методах.
Список литературы
-
https://studfile.net/preview/2455645/page:2/ – 28.04.2022 -
https://ru.wikipedia.org/wiki/Дихотомия – 28.04.2022 -
http://www.machinelearning.ru/wiki/ – 30.04.2022 -
http://statistica.ru/branches-maths/chislennye-metody-resheniya-uravneniy/ – 04.05.2022 -
https://ru.wikibooks.org/wiki/ – 04.05.2022 -
http://bpascal.ru/download/desc/319.php – 04.05.2022 -
https://academy.yandex.ru/posts/osnovnye-vidy-sortirovok-i-primery-ikh-realizatsii – 12.05.2022
приложение А
Листинг 1
#include
#include
using namespace std;
double f(double x)
{
double f;
f = x - exp(-x / 10);
return f;
}
void solve(double a, double b, double e)
{
setlocale(LC_ALL, "rus");
double x = 1;
int n;
if (f(a) * f(b) < 0)
{
n = 0;
while (1)
{
x = (a + b) / 2.0;
n++;
if (fabs(f(x)) < e) break;
if (f(a) * f(x) < 0)
{
a = a; b = x;
}
else
{
a = x; b = b;
}
cout << "n = " << n << "\t\t";
cout << "x = " << x << endl;
}
cout << "Корень x = " << x << endl;
cout << "Количество итераций n = " << n << endl;
}
}
int main()
{
double a, b, e, x;
int n;
setlocale(LC_ALL, "rus");
a = 0.0; b = 2.0; e = 0.00005;
cout << "В данной программе представлено решение нелинейного уравнения x - e^(-x/10) = 0\n";
cout << "Исходные данные:\n";
cout << "a = " << a << endl;
cout << "b = " << b << endl;
cout << "e = 0.00005" << endl;
cout << "Допустимое количество итераций n = 30" << endl;
solve(a, b, e);
}