ЛЕКЦИЯЛЫҚ КЕШЕН

Лекция 1
Тақырыбы: Жиындар, берілу тәсілдері.

Эйлер-Венн диаграммалары.

Жиындарға қолданылатын амалдар.

Жоспар

1. 
   Жиын ұғымы және жиынның элементтері.
   
2. 
   Жиынның берілу тәсілдері.
   
3. 
   Эйлер-Венн диаграммалары. Жиындарға амалдар қолдану және қасиеттері.
   
4. 
   Жиындардың толықтауышы және кластарға бөлу.
   

1. "Жиын" деген сөз математикада "көптіктің" мағынасында, оның бір баламасы ретінде қолданылады. Ол сөз жоғарыда айтқанымыздай "жинақ", "жиынтық" мағынасын білдіреді. Жиындар алуан-алуан объектілерден құралуы мүмкін, ол объектілер жиынның мүшелері немесе элементтері деп аталады. Мысалы, "адамдар жиыны" тірі табиғат объектілерінен құралса, "кітаптар жиыны" жансыз табиғат объектілерінен кұралады. Ал бүтін сандар жиынын алсақ, бұл жиын нақтылы объектілерден емес, дерексіз ұғымыдардан тұрады. Сөйтіп, не туралы пікір қорытып, ойлай алатын болсақ, солардың бәрі де жиын элементі бола алады. Сондай-ақ, жиын атаулының бәрі біртектес объектілерден кұралуы да шарт емес. Мысалы, элементтері оқушы, кітап, қалам, дәптер болатын жиын немесе үстел үстіндегі нәрселердің: шам, кітап, алма, қалам жиыны туралы сөз етуге болады. Жиын жалғыз ғана элементтен де құралуы мүмкін. Мысалы, Жердің барлық табиғи серіктерінің жиыны жалғыз серіктен - Айдан тұрады. Жиынның элементтерінің өздері жиындар болуы мүмкін. Мысалы, элементтерінің саны екіге тең жиындардың жиынын алатын болсақ, мұндай жиынның элементтері деп "су" сөзіндегі әріптер жиыны, адамның құлақтарының, көздерінің, қолдарының, құстың қанаттарының т.с.с. жиынын айтуға болады. Жиын латын алфавитінің үлкен әріптерімен A, B,C, ,….Z белгіленеді. Бір де бір элементі болмайтын жиынды құр (бос) жиын деп атайды. Оны Ø түрінде белгілейді. Жиынның элементтері латын алфавитінің кіші әріптерімен белгіленеді. Жиынның кез-келген элементінің ол жиынға жататындығы (тиістілігі) немесе оған жатпайтындығы (тиісті еместігі) тағайындалған болса, ондай жиын толығынан анықталған жиын деп аталады. а элементінің М жиынына жататындығын тиістілік таңбасы арқылы белгілейміз: а 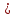М Бұлай белгілеуді сөзбен түрліше айтуға болады.

а дегеніміз М жиынының элементі;

а элементі М-ге тиісті ;

а

---

элементі М-ге енеді ;

а элементі М-нің құрамындағы элемент.

а элементінің М жиынына жатпайтындығын а М деп белгілеп, оны да әртүрлі оқуға болады:

а дегеніміз М жиынының элементі емес ;

а элементі М-ге тиісті емес ;

а элементі М-ге енбейді ;

а элементі М-нің құрамындағы элемент емес.

2. Егер жиын ақырлы санды элементтерден тұрса, оны ақырлы жиын деп атайды. Ақырлы жиын саналымды жиын деп те аталады. Өйткені оның барлық элементтерін "біртіндеп санап" шығуға, яғни тізбектей нөмірлеуге болады. Мысалы, а₁,а₂,а₃,...а_n, сонда барлық элемент те нөмірленіп, әртүрлі элемент түрліше нөмірленеді.

Егер жиын ақырсыз санды элементтерден тұрса, оны ақырсыз жиын деп атайды. Ақырсыз жиын элементтерін біртіндеп санап шығуға болмайды. Құр емес жиынның әртүрлі элементтері болмаса, ондай жиын бірлік жиын деп аталады. Сонымен, егер жалғыз а элементі болып, ол М жиынында жататын болса, онда М жиыны бір элементті жиын деп аталады. Мұны былай жазып көрсетеміз: М = а.

Жиын өзінің элементтері арқылы анықталады, яғни егер кез келген объект жөнінде ол осы жиынға тиісті немесе тиісті емес екендігін анықтауға болса, онда жиын берілген деп есептеледі.

1) Жиын оның барлық элементтерін тізіп көрсету арқылы беріледі. Мысалы, А жиыны 3, 4, 5, 6 элементтерінен тұрса, оның барлық элементтерін тізіп жазу арқылы көрсетуге болады. Мұндай жағдайда элементгер фигуралы жақшаға алынып А = {3, 4, 5, 6} түрінде жазылады. Бұл тәсілмен тек қана шектеулі жиындар беріледі.

Шексіз жиындарды тізіммен беру мүмкін емес. Мысалы, барлық тақ сандардын немесе екі нүктеден бірдей кашықтықта жататын нүктелердің жиынын тізім арқылы беру, яғни ол жиындардың барлық элементтерін тізіп жазу, мүмкін емес.

2) Мұндай жағдайда жиынды оның элементтеріиің сипаттамалық қасиеті арқылы береді.

Ол көрсетілген қасиет тек сол жиынның элементтеріне ғана тән болып, ал жиынның элементі бола алмайтын нәрселердің ешқайсысында ондай қасиет болмауы керек. Мысалы, eгер A жиыны екі орынды сандардың жиыны болса, 21 саны А жиынына тиісті, ал 145 саны екі орынды сан болмағандықтан А жиынына тиісті емес.

---

Жиынды элементтерінің сипаттамалық қасиеті арқылы беру геометрияда жиі қолданылады. Белгілі бір сипаттамалык касиеті бар нүктелердің жиынын нүктелердің геометриялық орны дейміз.

Кейде бір жиынды оның барлық элементтерінің тізімі арқылы да немесе сипаттамалық қасиеті арқылы да беруге болады. Мысалы: В = {1, 3, 5, 7, 9} жиыны тізім арқылы беріліп тұр. Ал осы жиынды сипаттамалық қасиетін көрсету арқылы да, яғни "бір таңбалы тақ сандардың жиыны" деп беруге де болады.

Кейбір жағдайдарда, әртүрлі сипаттамалық касиеттер бір ғана жиынды анықтауы мүмкін. Мысалы, А жиыны бірдей екі цифрдан құралған екі таңбалы сандардың жиыны болсын: A = {11, 22, 33, 44, 55, 66, 77, 88, 99}

Бұл жиынды 11 -ге бөлінетін екі таңбалы сандардың жиыны ретінде де анықтауға болады.

Шексіз жиындарды да фигуралы жақша арқылы көп нүктені пайдаланып белгілеуге болады. Мысалы, натурал сандар жиынын былай, N = {1, 2, 3, …n…} белгілейміз.

Сипаттамалық қасиеті бойынша анықталған элементтердің жиынын былай белгілеуге болады: фигуралы жақшаның ішінде алдымен жиынның элементін белгілейтін әріп жазылып, тік сызықтан кейін сипаттамалық қасиет жазылады. Мысалы, А = {x |x = 3k, k z|}, бұл А жиыны барлық 3-ке еселі сандардың жиыны екендігін көрсетеді.

3. А = {a, b, с, d, е} және в = {b, d, к, f} жиындары берілсін. b мен J элементтері А және В жиындарында жататынын көреміз. b мен J элементтерін А және В жиындарының ортақ элементтері деп атап, бұл жиындарды қиылысады дейді.

Егер жиындардың ортақ элементтері болмаса, онда оларды қиылыспайды дейді.

Енді A = {a, b, c, d, e} және в = {c, d, e} жиындарын қарастырайық. Бұл жиындар қиылысады, сонымен қатар В жиынының барлық элементтері А жиынының да элементтері болып табылады.

Анықтама: Егер В жиынының әрбір элементі A жиынының да элементі болса, онда В жиыны А жиынының ішкі жиыны деп аталады. Бұл қатыс былай жазылады

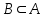
Оқылуы: В жиыны А жиынында қамтылған немесе В жиыны A жиынының ішкі жиыны.

_{Мысалы, егер А мектептегі бесінші сынып оқушыларының жиыны, ал В- осы сыныптағы ер балалар жиыны болса, онда В жиыны А жиынының ішкі жиыны болады, яғни .}

---

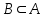Құр жиын кез-келген жиынның ішкі жиыны болады, яғни 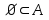сонымен қатар жиын өзінің де ішкі жиыны болады, .

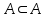Анықтама. Егер А жиынының әрбір элементі В жиынының да элементі болса және керісінше, В жиынының әрбір элементі А жиынының да элементі болса, онда А мен В жиындары тең деп аталады да былай жазылады: А = В.

Бұл анықтаманы былай да айтуға болады: егер 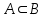және 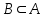болса, онда А және В жиындары тең деп аталады.

Көрнекілік үшін жиындарды дөңгелек не сопақ тәрізді фигуралармен бейнелейді. Оның ішінде сол жиынның элементтері ғана орналасады. Ол дөңгелектерді Эйлер дөңгелектері деп атайды.

Мысалы, A = {a, b, c, d, e}, B = {c, d, e} болса, В жиыны A жиынында қамтылады (ішкі жиыны болады) деген қатысты Эйлер дөңгелегі арқылы 1 сызбадағыдай көрсетіледі.

A = {a, b, c, d, e}, B = {b, d, k, e} жиындары қиылысады, бірақ біреуі екіншісінің ішкі жиыны болмайды. Сондықтан олар Эйлер дөңгелегі арқылы 2 сызбадағыдай бейнеленеді.

Қиылыспайтын жиындар ортақ нүктелері болмайтын екі дөңгелек арқылы көрсетіледі. (3-сызба)



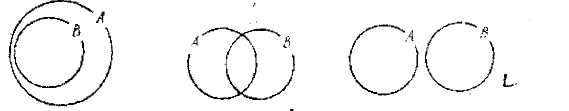
1-сызба 2-сызба 3-сызба
A = {2, 4, 6, 8} және B = {5, 6, 7, 8, 9} жиындары берілсін. А және В жиындарының ортақ элементтерінен тұатын С жиынын құрайық, С = {6, 8}. Сонымен алынған С жиыны А және В жиындарының қиылысуы деп аталады.

Анықтама: А жиынына да В жиынына да тиісті элементтерден тұратын С жиынын А және В жиындарының қиылысуы деп атайды.

А және В жиындарының қиылысуы былай белгіленеді: 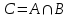. Егер А, В жиындарын Эйлер дөңгелегі арқылы бейнелесек, екі жиынның қиылысуы 4- сызбадағы штрихталған облыс болады.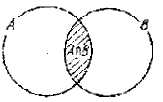



4 сызба.

Анықтама. А және В екі жиынның бірігуі деп олардың ең болмағанда біреуіне тиісті элементтерден тұратын жиынды айтады. Екі жиынның бірігуі былай белгіленеді: .

---

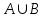Егер қиылысатын А мен В жиындарын Эйлер дөңгелегі арқылы бейнелесек, онда олардың бірігуі 5- сызбадағыдай штрихталған облысты береді. А және В жиындары қиылыспаса, онда олардың бірігуі 6 -сызбадағыдай бейнеленеді. Егер А және В жиындарының элементтері тізіммен берілсе, элементтерін табу үшін осы екі жиынның ең болмағанда біреуінде жататын элементтердін тізімін жазу керек. болсын, сонда ={2, 4, 5, 6, 7, 8, 9} болады.



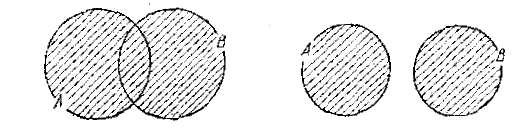
5-сызба 6-сызба





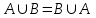
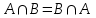
Бұл жиындардың бірігуі мен қиылысуы үшін ауыстырымдылық заңының тура екендігін көрсетеді.

Кез келген А, В, С жиындарының бірігуі мен қиылысуы үшін терімділік заңы тура болады:





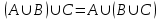
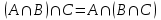
Егер қарастырылған мысалды жалпыласақ мынаған келеміз: а элементтен тұратын жиыннан b элементтен тұратын оның ішкі жиынын шығарып тастасақ қалған жиын a - ь элементтен тұрады.

Эйлер дөңгелегінің көмегімен оны 10 – сызбадағыдай кескіндеуге болады, мұндағы штрихталған бөлік А жиынынан В жиынын


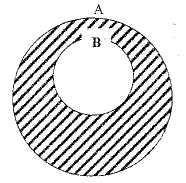
10 – сызбы.

шығарып тастағандағы жиынға сәйкес келеді.

Осы бөлікті В жиынының А жиынына дейінгі толықтауышы деп атайды.

4. Анықтама: болсын. А жиынының В жиынына тиіс ті емес элементтерінің жиыиын В жиынының А жиынына дейінгі толықтауышы деп атайды.

Жиынның толықтауышын табу амалы жиындарды азайту деп аталып, а/в түрінде белгіленеді.

Кез-келген классификация қандай-да бір объектілер жиынын ішкі жиындарға жіктеумен байланысты. Бұл жағдайда әрбір элемент ішкі жиындардың тек біреуіне ғана тиісті болады, ал барлық алынған ішкі жиындардын бірігуі берілген жиынмен беттеседі, сонда берілген жиынды қиылыспайтын ішкі жиындарға немесе кластарға бөлінді деп айтады.

---

Смотрите также файлы

• Язык танца Содержание.pptx

• Проверочный тест Августин и Фома Аквинский.docx

• Контрольная работа по дисциплине Библиотековедение Лапчук И. А., студентка 2ого курса, заочного отделения.docx

• Тестовое задание для 10 б класса Задание.docx

• Практическая работа Приемка товаров по количеству Цель приобрести навыки в документальном оформлении результатов приемки.docx