Добавлен: 04.12.2023
Просмотров: 115
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
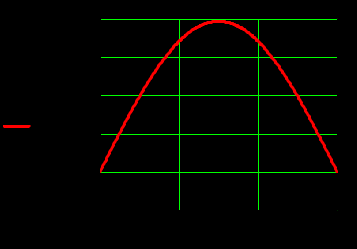
Рисунок 7-12
3. Графики зависимостей амплитуд составляющих векторов поля от координаты z вдоль линии x=0.5a; y=0.25b в интервале
на частоте 
, рисунки 13-18.  |  |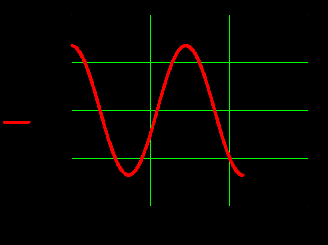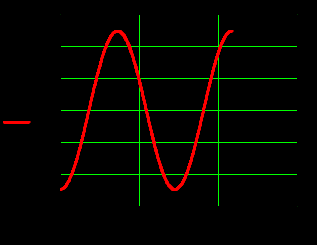
 |  |
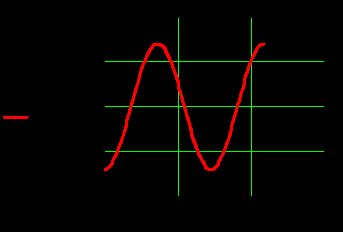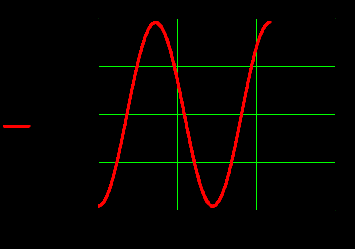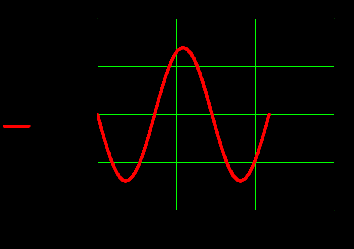
Рисунок 19-23
4.Графики зависимостей амплитуд составляющих векторов поля от координаты z вдоль линии x=0.5a; y=0.25b в интервале
на частоте 
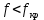, рисунки 24-28.  |  |
 |  |
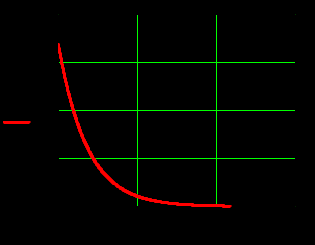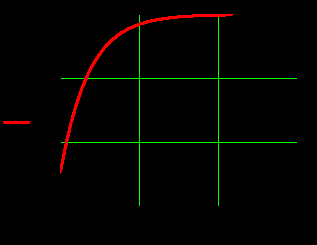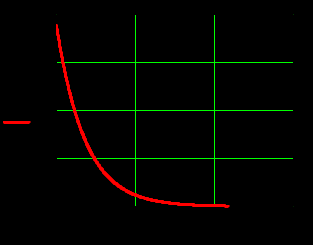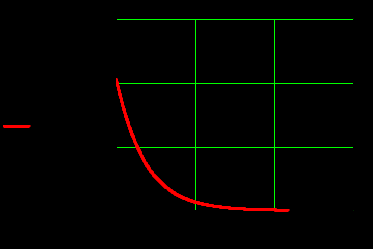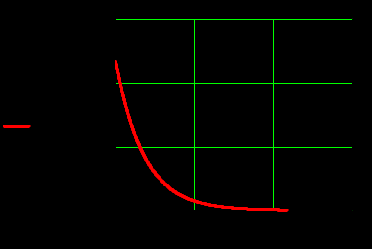
5. Проверить выполнение граничных условий для касательных составляющих вектора
и нормальной составляющей вектора 
на верхней (y=b) стенке трубы.Проверка граничных условий заключается в проверке истинности утверждени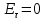й
и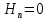 
, т.е. равенста нулю касательной вектора и нормальной вектора проекций (составляющих).Для верхней стенки волновода (y=b), касательными составляющими вектора электрического поля являются составляющие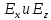 
, а нормальной составляющей вектора магнитного поля является составляющая 
.
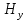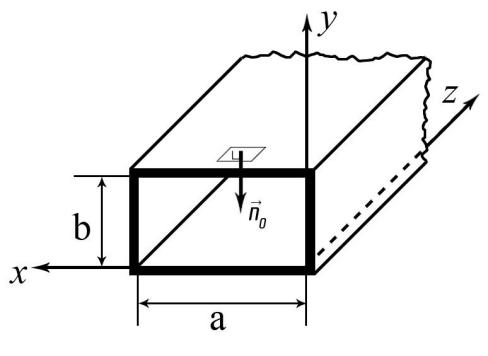
Рисунок 29
Возьмем необходимые ненулевые составляющие и подставим y=b.
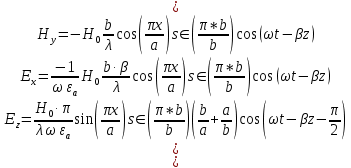
Получаем, что:
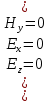
Таким образом, граничные условия на верхней стенке трубы волновода выполняются.
6. Найти комплексные амплитуды плотностей поверхностных токов и зарядов на боковой (x=a) стенке трубы.
Комплексную амплитуду поверхностного тока можно найти по формуле:
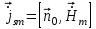
Комплексную амплитуду плотности зарядов можно найти по формуле:
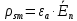
Для левой стенки волновода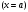 
нормаль противоположна вектору 
: 
.
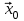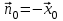
Рисунок 30
Касательными к этой стенке составляющими вектора
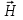являются составляющие вдоль осей y и z, то есть: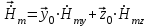
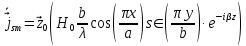
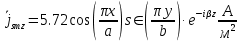
Нормальной к этой стенке составляющей вектора
будет составляющая 
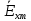. Тогда комплексная амплитуда плотности поверхностных зарядов будет равна: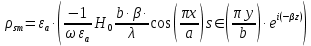
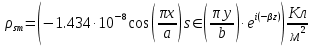
7. Вычислить средние за период значения объемных плотностей энергий электрического и магнитного полей.
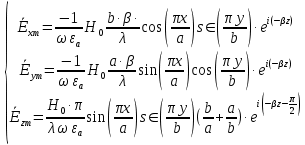
Объемная плотность энергии может быть найдена по формулам:
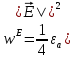
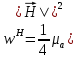
В данном случае, преобразуем эти выражения следующим образом:
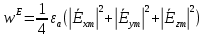
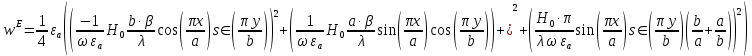
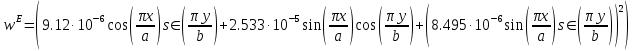
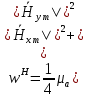
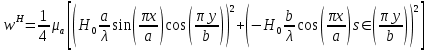
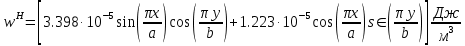
8. Записать выражение для комплексного вектора Пойтинга для двух случаев: когда частота принадлежит найденному в п. 2 диапазону и когда она не принадлежит этому диапазону. Определить среднее за период значение плотности потока энергии и амплитуду плотности реактивного потока энергии.
Комплексное значение вектора Пойнтинга запишем по формуле:
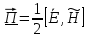
Где
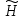
-комплексно-сопряженное выражение
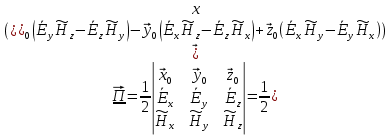
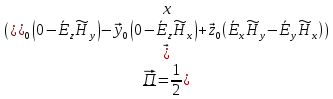
а) Рассмотрим режим бегущей волны:
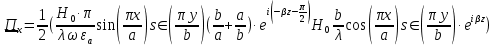
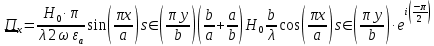
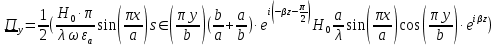
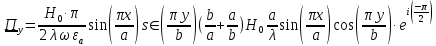
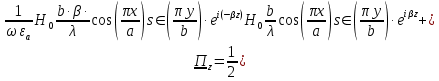
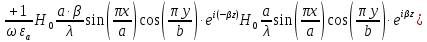
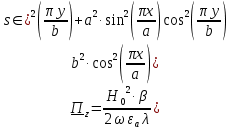
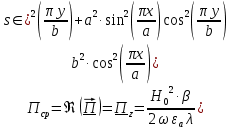
Cоставляющие по оси x, y чисто мнимые, следовательно:
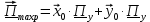
б) Во втором случае (f
В этом случае вектор Пойтинга чисто мнимый и переноса энергии не происходит.
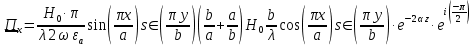
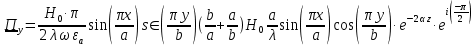
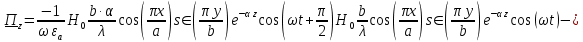
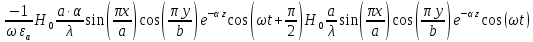
9. Записать выражения для мгновенных значений плотностей активного и реактивного потоков энергии для двух случаев, указанных п.8
Запись выражений для мгновенного значения вектора Пойнтинга:
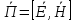
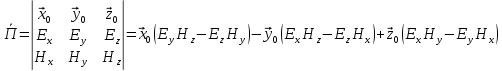
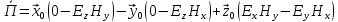
а) Рассмотрим режим бегущей волны:
 | |
 | |
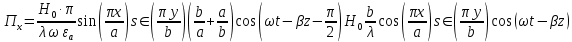
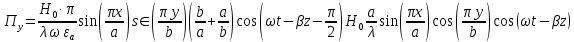
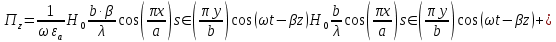
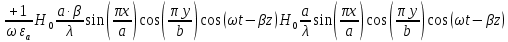
б) Во втором случае (f
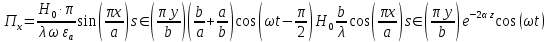
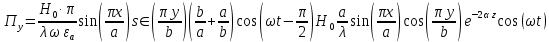
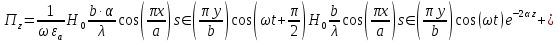
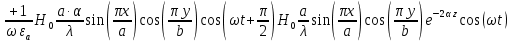
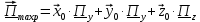
10. Вычислить средний за период поток энергии через поперечное сечение трубы.
Мощность за период потока энергии через поперечное сечение волновда определяется по формуле:
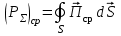
Вычисления производим на частоте f (
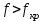)Выражения для среднего значения вектора Пойнтинга найдем по формуле:
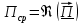
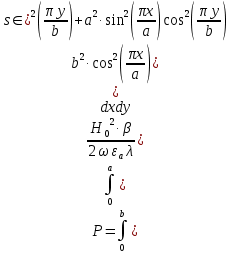
Расчет произведём в MathCad:
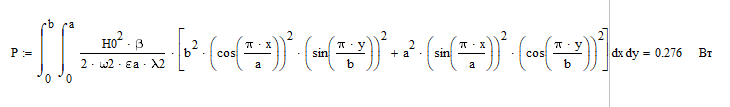
11. Определить фазовую скорость
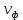и скорость распространения энергии 
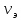рассматриваемой волны. Рассчитать и построить графики зависимосте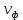й и 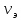от частоты. Фазовую скорость вычисляем по формуле: