Файл: Решение Сначала построим график функции и определим интервалы нахождении корней уравнения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Для удобства представим результаты в виде таблицы
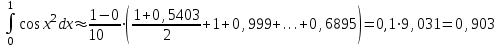
5. Применяя методы Эйлера и Рунге–Кутта решить уравнения (а), (б) (число шагов для каждого уравнения n = 15).
а)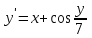
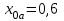
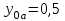
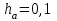
Решение:
Метод Эйлера:
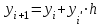
Т.к.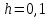 и
и 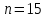 , то:
, то:
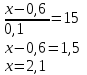
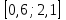 - отрезок.
- отрезок.
Оформим в таблице:
Метод Рунге-Кутта:
б)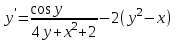
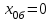
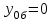
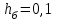
Решение:
Метод Эйлера:

Т.к. и
и  , то:
, то:
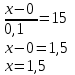
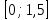 - отрезок.
- отрезок.
Оформим в таблице:
Метод Рунге-Кутта:
Для удобства представим результаты в виде таблицы
| i | xi | yi |
| 0 | 0 | 1 |
| 1 | 0,1 | 1 |
| 2 | 0,2 | 0,9992 |
| 3 | 0,3 | 0,996 |
| 4 | 0,4 | 0,9872 |
| 5 | 0,5 | 0,9689 |
| 6 | 0,6 | 0,9359 |
| 7 | 0,7 | 0,8823 |
| 8 | 0,8 | 0,8021 |
| 9 | 0,9 | 0,6895 |
| 10 | 1 | 0,5403 |
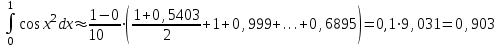
5. Применяя методы Эйлера и Рунге–Кутта решить уравнения (а), (б) (число шагов для каждого уравнения n = 15).
а)
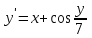
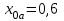
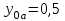
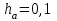
Решение:
Метод Эйлера:
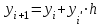
Т.к.
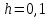 и
и 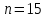 , то:
, то: 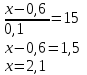
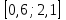 - отрезок.
- отрезок.Оформим в таблице:
| i | xi | yi | y' |
| 0 | 0,6 | 0,5 | 1,597450064 |
| 1 | 0,7 | 0,659745006 | 1,695561823 |
| 2 | 0,8 | 0,829301189 | 1,792990445 |
| 3 | 0,9 | 1,008600233 | 1,889637595 |
| 4 | 1 | 1,197563993 | 1,985401378 |
| 5 | 1,1 | 1,39610413 | 2,080176996 |
| 6 | 1,2 | 1,60412183 | 2,173857493 |
| 7 | 1,3 | 1,821507579 | 2,266334589 |
| 8 | 1,4 | 2,048141038 | 2,357499591 |
| 9 | 1,5 | 2,283890997 | 2,447244394 |
| 10 | 1,6 | 2,528615437 | 2,535462544 |
| 11 | 1,7 | 2,782161691 | 2,622050369 |
| 12 | 1,8 | 3,044366728 | 2,706908163 |
| 13 | 1,9 | 3,315057544 | 2,789941405 |
| 14 | 2 | 3,594051685 | 2,871062004 |
| 15 | 2,1 | 3,881157885 | |
Метод Рунге-Кутта:
| i | h | xi | yi | f(xi, yi) | k1 | f(xi+h/2, yi+k1/2) | k2 | f(xi+h/2, yi+k2/2) | k3 | f(xi+h, yi+k3) | k4 | dyi |
| 0 | 0,1 | 0,6 | 0,5000 | 1,5975 | 0,1597 | 1,6328 | 0,1633 | 1,6465 | 0,1647 | 1,6955 | 0,1695 | 0,1370 |
| 1 | 0,1 | 0,7 | 0,6370 | 1,6959 | 0,1696 | 1,7276 | 0,1728 | 1,7447 | 0,1745 | 1,7933 | 0,1793 | 0,1451 |
| 2 | 0,1 | 0,8 | 0,7821 | 1,7938 | 0,1794 | 1,8214 | 0,1821 | 1,8422 | 0,1842 | 1,8905 | 0,1890 | 0,1532 |
| 3 | 0,1 | 0,9 | 0,9353 | 1,8911 | 0,1891 | 1,9141 | 0,1914 | 1,9392 | 0,1939 | 1,9870 | 0,1987 | 0,1612 |
| 4 | 0,1 | 1 | 1,0964 | 1,9878 | 0,1988 | 2,0057 | 0,2006 | 2,0354 | 0,2035 | 2,0828 | 0,2083 | 0,1691 |
| 5 | 0,1 | 1,1 | 1,2655 | 2,0837 | 0,2084 | 2,0962 | 0,2096 | 2,1309 | 0,2131 | 2,1778 | 0,2178 | 0,1770 |
| 6 | 0,1 | 1,2 | 1,4425 | 2,1788 | 0,2179 | 2,1853 | 0,2185 | 2,2255 | 0,2226 | 2,2718 | 0,2272 | 0,1848 |
| 7 | 0,1 | 1,3 | 1,6273 | 2,2731 | 0,2273 | 2,2731 | 0,2273 | 2,3192 | 0,2319 | 2,3649 | 0,2365 | 0,1925 |
| 8 | 0,1 | 1,4 | 1,8198 | 2,3664 | 0,2366 | 2,3594 | 0,2359 | 2,4119 | 0,2412 | 2,4570 | 0,2457 | 0,2001 |
| 9 | 0,1 | 1,5 | 2,0199 | 2,4587 | 0,2459 | 2,4442 | 0,2444 | 2,5035 | 0,2504 | 2,5479 | 0,2548 | 0,2076 |
| 10 | 0,1 | 1,6 | 2,2276 | 2,5498 | 0,2550 | 2,5274 | 0,2527 | 2,5940 | 0,2594 | 2,6375 | 0,2638 | 0,2150 |
| 11 | 0,1 | 1,7 | 2,4426 | 2,6397 | 0,2640 | 2,6090 | 0,2609 | 2,6832 | 0,2683 | 2,7259 | 0,2726 | 0,2224 |
| 12 | 0,1 | 1,8 | 2,6649 | 2,7284 | 0,2728 | 2,6889 | 0,2689 | 2,7711 | 0,2771 | 2,8130 | 0,2813 | 0,2295 |
| 13 | 0,1 | 1,9 | 2,8945 | 2,8157 | 0,2816 | 2,7670 | 0,2767 | 2,8576 | 0,2858 | 2,8986 | 0,2899 | 0,2366 |
| 14 | 0,1 | 2 | 3,1311 | 2,9016 | 0,2902 | 2,8433 | 0,2843 | 2,9426 | 0,2943 | 2,9826 | 0,2983 | 0,2435 |
| 15 | 0,1 | 2,1 | 3,3746 | | | | | | | | | |
б)
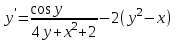
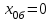
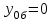
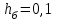
Решение:
Метод Эйлера:

Т.к.
 и
и  , то:
, то: 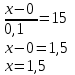
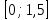 - отрезок.
- отрезок.Оформим в таблице:
| i | xi | yi | y' |
| 0 | 0 | 0 | 0,5 |
| 1 | 0,1 | 0,05 | 0,646923195 |
| 2 | 0,2 | 0,114692319 | 0,771259079 |
| 3 | 0,3 | 0,191818227 | 0,869976625 |
| 4 | 0,4 | 0,27881589 | 0,938051533 |
| 5 | 0,5 | 0,372621043 | 0,971305987 |
| 6 | 0,6 | 0,469751642 | 0,969018136 |
| 7 | 0,7 | 0,566653455 | 0,935182257 |
| 8 | 0,8 | 0,660171681 | 0,877927051 |
| 9 | 0,9 | 0,747964386 | 0,807450313 |
| 10 | 1 | 0,828709418 | 0,733503561 |
| 11 | 1,1 | 0,902059774 | 0,663508191 |
| 12 | 1,2 | 0,968410593 | 0,601834859 |
| 13 | 1,3 | 1,028594079 | 0,550108221 |
| 14 | 1,4 | 1,083604901 | 0,508041911 |
| 15 | 1,5 | 1,134409092 | |
Метод Рунге-Кутта:
| i | h | xi | yi | f(xi, yi) | k1 | f(xi+h/2, yi+k1/2) | k2 | f(xi+h/2, yi+k2/2) | k3 | f(xi+h, yi+k3) | k4 | dyi |
| 0 | 0,1 | 0 | 0,5000 | -0,2806 | -0,0281 | -0,1483 | -0,0148 | -0,1635 | -0,0163 | -0,0434 | -0,0043 | -0,0133 |
| 1 | 0,1 | 0,1 | 0,4867 | -0,0503 | -0,0050 | 0,0547 | 0,0055 | 0,0427 | 0,0043 | 0,1382 | 0,0138 | 0,0038 |
| 2 | 0,1 | 0,2 | 0,4905 | 0,1393 | 0,0139 | 0,2220 | 0,0222 | 0,2123 | 0,0212 | 0,2871 | 0,0287 | 0,0179 |
| 3 | 0,1 | 0,3 | 0,5084 | 0,2950 | 0,0295 | 0,3582 | 0,0358 | 0,3506 | 0,0351 | 0,4069 | 0,0407 | 0,0294 |
| 4 | 0,1 | 0,4 | 0,5377 | 0,4210 | 0,0421 | 0,4666 | 0,0467 | 0,4609 | 0,0461 | 0,5003 | 0,0500 | 0,0385 |
| 5 | 0,1 | 0,5 | 0,5762 | 0,5201 | 0,0520 | 0,5496 | 0,0550 | 0,5456 | 0,0546 | 0,5696 | 0,0570 | 0,0455 |
| 6 | 0,1 | 0,6 | 0,6217 | 0,5946 | 0,0595 | 0,6094 | 0,0609 | 0,6073 | 0,0607 | 0,6172 | 0,0617 | 0,0506 |
| 7 | 0,1 | 0,7 | 0,6723 | 0,6470 | 0,0647 | 0,6485 | 0,0648 | 0,6482 | 0,0648 | 0,6457 | 0,0646 | 0,0540 |
| 8 | 0,1 | 0,8 | 0,7263 | 0,6799 | 0,0680 | 0,6697 | 0,0670 | 0,6714 | 0,0671 | 0,6582 | 0,0658 | 0,0558 |
| 9 | 0,1 | 0,9 | 0,7821 | 0,6960 | 0,0696 | 0,6762 | 0,0676 | 0,6796 | 0,0680 | 0,6578 | 0,0658 | 0,0565 |
| 10 | 0,1 | 1 | 0,8386 | 0,6987 | 0,0699 | 0,6712 | 0,0671 | 0,6762 | 0,0676 | 0,6477 | 0,0648 | 0,0562 |
| 11 | 0,1 | 1,1 | 0,8948 | 0,6909 | 0,0691 | 0,6577 | 0,0658 | 0,6642 | 0,0664 | 0,6308 | 0,0631 | 0,0551 |
| 12 | 0,1 | 1,2 | 0,9499 | 0,6757 | 0,0676 | 0,6386 | 0,0639 | 0,6462 | 0,0646 | 0,6096 | 0,0610 | 0,0536 |
| 13 | 0,1 | 1,3 | 1,0035 | 0,6557 | 0,0656 | 0,6161 | 0,0616 | 0,6246 | 0,0625 | 0,5862 | 0,0586 | 0,0518 |
| 14 | 0,1 | 1,4 | 1,0553 | 0,6330 | 0,0633 | 0,5922 | 0,0592 | 0,6013 | 0,0601 | 0,5621 | 0,0562 | 0,0498 |
| 15 | 0,1 | 1,5 | 1,1051 | | | | | | | | | |