Файл: Решение Сначала построим график функции и определим интервалы нахождении корней уравнения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 47
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
в последний раз пересечет область допустимых решений, функция z достигает своего наибольшего значения.
Функция z достигает наибольшего значения в точке A.
Координаты точки A (52/3, 11/3).
Вычислим значение функции z в точке A (52/3, 11/3):
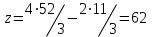
Найдем минимум функции. Решим задачу графически.
Строим область ограничения функции и целевую функцию.
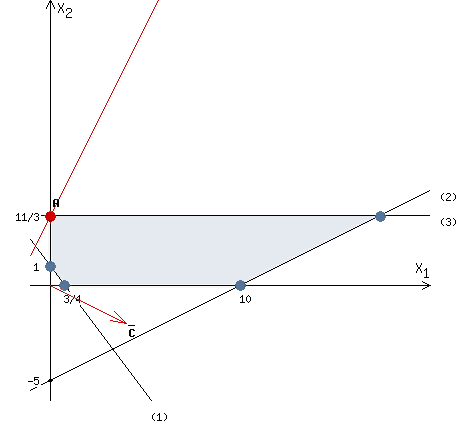
Прямую
будем двигать параллельно до первого касания с нашей областью ограничения. В точке, в которой прямая в первый раз пересечет область допустимых решений, функция z достигает своего наименьшего значения.
Функция z достигает наименьшего значения в точке A.
Координаты точки A (0,11/3).
Вычислим значение функции z в точке A (0,11/3):
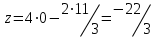
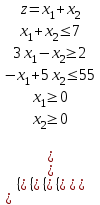
Решение:
Найдем максимум функции. Решим задачу графически.
Строим область ограничения функции и целевую функцию.
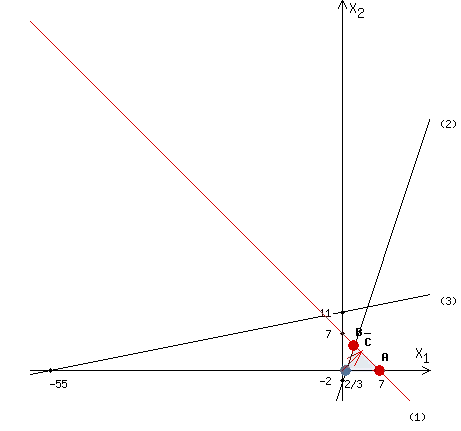
Прямую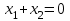
будем двигать параллельно до последнего касания с нашей областью ограничения. В точке, в которой прямая 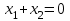в последний раз пересечет область допустимых решений, функция z достигает своего наибольшего значения.
Координаты точки A (7,0)
Вычислим значение функции F в точке A (7,0):
z(A) = 1 * 7 + 1 * 0 = 7
Найдем координаты точки B: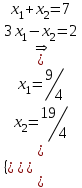
Вычислим значение функции F в точке B (9/4,19/4):
z(B) = 1 * 9/4 + 1 * 19/4 = 7
F(A) = F(B)
Значит, функция F достигает своего наибольшего значения в любой точке отрезка AB.
Найдем минимум функции. Решим задачу графически.
Строим область ограничения функции и целевую функцию.
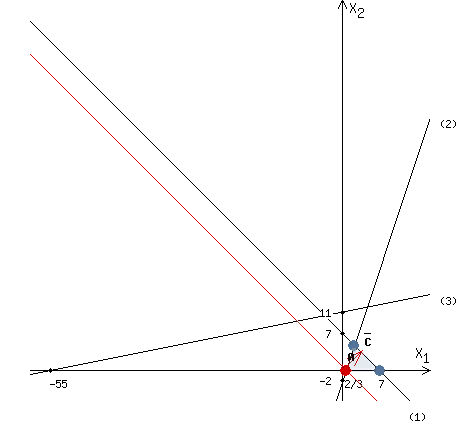
Прямую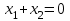 будем двигать параллельно до первого касания с нашей областью ограничения. В точке, в которой прямая
в первый раз пересечет область допустимых решений, функция z достигает своего наименьшего значения.
Функция z достигает наименьшего значения в точке A.
Координаты точки A (2/3, 0).
Вычислим значение функции z в точке A (2/3, 0):
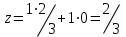
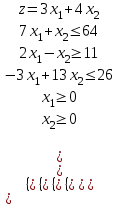
Решение:
Находим максимум функции, решаем Симплекс-методом:
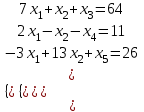
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Оптимальный план можно записать так: x1 = 827/47, x2 = 346/47.
zmax = 3*827/47 + 4*346/47 = 4130/47
Найдем минимум функции:
Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи.
Оптимальный план можно записать так:
x1 = 51/2, x2 = 0.
zmin = 3*51/2 + 4*0 = 161/2.
Функция z достигает наибольшего значения в точке A.
Координаты точки A (52/3, 11/3).
Вычислим значение функции z в точке A (52/3, 11/3):
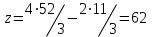
Найдем минимум функции. Решим задачу графически.
Строим область ограничения функции и целевую функцию.
Прямую
будем двигать параллельно до первого касания с нашей областью ограничения. В точке, в которой прямая в первый раз пересечет область допустимых решений, функция z достигает своего наименьшего значения.Функция z достигает наименьшего значения в точке A.
Координаты точки A (0,11/3).
Вычислим значение функции z в точке A (0,11/3):
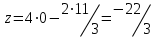
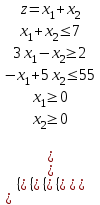
Решение:
Найдем максимум функции. Решим задачу графически.
Строим область ограничения функции и целевую функцию.
Прямую
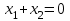будем двигать параллельно до последнего касания с нашей областью ограничения. В точке, в которой прямая 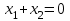в последний раз пересечет область допустимых решений, функция z достигает своего наибольшего значения.Координаты точки A (7,0)
Вычислим значение функции F в точке A (7,0):
z(A) = 1 * 7 + 1 * 0 = 7
Найдем координаты точки B:
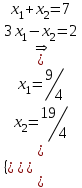
Вычислим значение функции F в точке B (9/4,19/4):
z(B) = 1 * 9/4 + 1 * 19/4 = 7
F(A) = F(B)
Значит, функция F достигает своего наибольшего значения в любой точке отрезка AB.
Найдем минимум функции. Решим задачу графически.
Строим область ограничения функции и целевую функцию.
Прямую
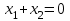будем двигать параллельно до первого касания с нашей областью ограничения. В точке, в которой прямая
в первый раз пересечет область допустимых решений, функция z достигает своего наименьшего значения.Функция z достигает наименьшего значения в точке A.
Координаты точки A (2/3, 0).
Вычислим значение функции z в точке A (2/3, 0):
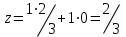
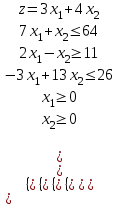
Решение:
Находим максимум функции, решаем Симплекс-методом:
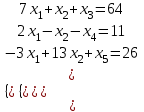
| 7 | 1 | 1 | 0 | 0 | 64 |
| -2 | 1 | 0 | 1 | 0 | -11 |
| -3 | 13 | 0 | 0 | 1 | 26 |
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
| Базис | B | x1 | x2 | x3 | x4 | x5 | min |
| x3 | 51/2 | 0 | 9/2 | 1 | 7/2 | 0 | 17/3 |
| x1 | 11/2 | 1 | -1/2 | 0 | -1/2 | 0 | - |
| x5 | 85/2 | 0 | 23/2 | 0 | -3/2 | 1 | 85/23 |
| z | 0 | 0 | -11/2 | 0 | -3/2 | 0 | 0 |
| Базис | B | x1 | x2 | x3 | x4 | x5 | min |
| x3 | 204/23 | 0 | 0 | 1 | 94/23 | -9/23 | 102/47 |
| x1 | 169/23 | 1 | 0 | 0 | -13/23 | 1/23 | - |
| x2 | 85/23 | 0 | 1 | 0 | -3/23 | 2/23 | - |
| z | 935/46 | 0 | 0 | 0 | -51/23 | 11/23 | 0 |
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x4 | 102/47 | 0 | 0 | 23/94 | 1 | -9/94 |
| x1 | 403/47 | 1 | 0 | 13/94 | 0 | -1/94 |
| x2 | 187/47 | 0 | 1 | 3/94 | 0 | 7/94 |
| z | 2363/94 | 0 | 0 | 51/94 | 0 | 25/94 |
Оптимальный план можно записать так: x1 = 827/47, x2 = 346/47.
zmax = 3*827/47 + 4*346/47 = 4130/47
Найдем минимум функции:
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x3 | 51/2 | 0 | 9/2 | 1 | 7/2 | 0 |
| x1 | 11/2 | 1 | -1/2 | 0 | -1/2 | 0 |
| x5 | 85/2 | 0 | 23/2 | 0 | -3/2 | 1 |
| z | -33/2 | 0 | 11/2 | 0 | 3/2 | 0 |
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x3 | 51/2 | 0 | 9/2 | 1 | 7/2 | 0 |
| x1 | 11/2 | 1 | -1/2 | 0 | -1/2 | 0 |
| x5 | 85/2 | 0 | 23/2 | 0 | -3/2 | 1 |
| z | 0 | 0 | -11/2 | 0 | -3/2 | 0 |
Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи.
Оптимальный план можно записать так:
x1 = 51/2, x2 = 0.
zmin = 3*51/2 + 4*0 = 161/2.