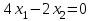6. Найти минимум заданной целевой функции в заданном интервале с заданной точностью: в интервале [0, 10], = 0,1.Решение:Используем для этого Метод золотого сечения.Положим: a₁ = a, b₁ = b. Вычислим: λ₁ = a₁ + (1 – 0,618)*(b₁ – a₁) = 3,82, μ₁ = a₁ + 0,618*(b₁ – a₁) = 6,18.Вычислим: f(λ₁) = 1476,0303, f(μ₁) = 196505327,9042Поскольку: f(λ₁) < f(μ₁), то b₂ = 6,18, a₂ = a₁, μ₂ = 3,82, f(μ₂) =196505327,9042λ₂ = a₂ + (1 – 0,618)*(b₂ – a₂) = 0 + (1 – 0,618)*(6,18 – 0) = 3,82, f(3,82) = 1476,0303Поскольку f(λ₂) < f(μ₂), то b₃ = 3,82, a₃ = a₂, μ₃ = 2,3608, f(μ₃) =1476,0303λ₃ = a₃ + (1 – 0,618)*(b₃ – a₃) = 0 + (1 – 0,618)*(3,82 – 0) = 2,3608, f(2,3608) = 17,0429Поскольку f(λ₃) < f(μ₃), то b₄ = 2,3608, a₄ = a₃, μ₄ = 1,4592, f(μ₄) = 17,0429λ₄ = a₄ + (1 – 0,618)*(b₄ – a₄) = 0 + (1 – 0,618)*(2.3608 – 0) = 1,4592, f(1,4592) = 7,6478Поскольку f(λ₄) > f(μ₄), то a₅ = 0,9018, b₅ = b₄, λ₅ = 1,4592, f(λ₅) = 10,3065

---

μ₅ = a₅ + 0,618*(b₅ – a₅) = 0,9018 + 0,618*(2,3608 – 0,9018) = 1,8034, f(1,8034) = 7,6478Остальные расчеты сведем в таблицу:

N	an	bn	bn-an	λn	μn	F(λn)	F(μn)
1	0	10	10	3,82	6,18	1476,0303	196505327,9042
2	0	6,18	6,18	2,3608	3,82	17,0429	1476,0303
3	0	3,82	3,82	1,4592	2,3608	7,6478	17,0429
4	0	2,3608	2,3608	0,9018	1,4592	10,3065	7,6478
5	0,9018	2,3608	1,4589	1,4592	1,8034	7,6478	7,948
6	0,9018	1,8034	0,9016	1,2462	1,4592	8,3254	7,6478
7	1,2462	1,8034	0,5572	1,4592	1,5906	7,6478	7,5159
8	1,4592	1,8034	0,3442	1,5906	1,672	7,5159	7,5734
9	1,4592	1,672	0,2127	1,5405	1,5906	7,5361	7,5159
10	1,5405	1,672	0,1315	1,5906	1,6217	7,5159	7,524
11	1,5405	1,6217	0,08124	1,5715	1,5906	7,5189	7,5159

---

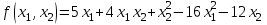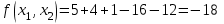
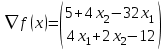
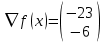
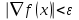
|7,5179 – 7,5167| ≤ 0,1Находим x как середину интервала [a, b]: x = (1,6217 + 1,5405)/2 = 1,5811183883908Ответ: x = 1,5811183883908; F(x) = 7,51677. 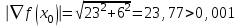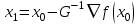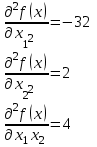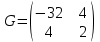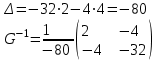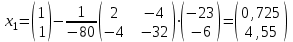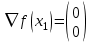Найти минимум многомерной целевой функции с заданной точностью: , Решение:Вычислим значение функции в начальной точке:В качестве направления поиска выберем вектор градиент в текущей точке:Значение градиента в точке X₀: Проверим критерий остановки: Имеем: Сделаем шаг вдоль ньютоновского направления:Найдем матрицу Гессе и обратный гессиан:Матрица Гессе: Обратный гессиан:Получим:В этой точке 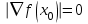и матрица Гессе положительно определена, следовательно,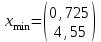

---

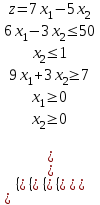
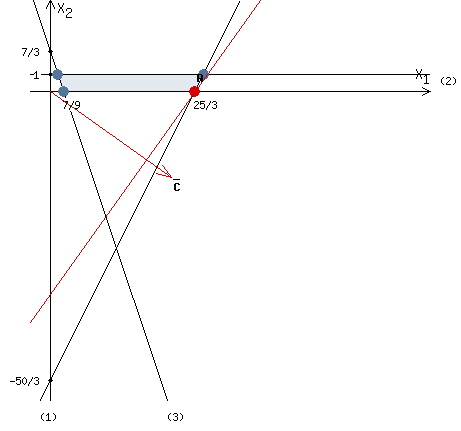
8. Решить стандартную задачу линейного программирования:Решение:Найдем максимум функции. Решим задачу графически.Строим область ограничения функции и целевую функцию. Прямую 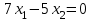будем двигать параллельно до последнего касания с нашей областью ограничения. 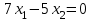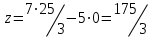В точке, в которой прямая в последний раз пересечет область допустимых решений, функция z достигает своего наибольшего значения.Функция z достигает наибольшего значения в точке A.Координаты точки A (25/3,0).Вычислим значение функции z в точке A (25/3,0):Найдем минимум функции. Решим задачу графически.Строим область ограничения функции и целевую функцию. 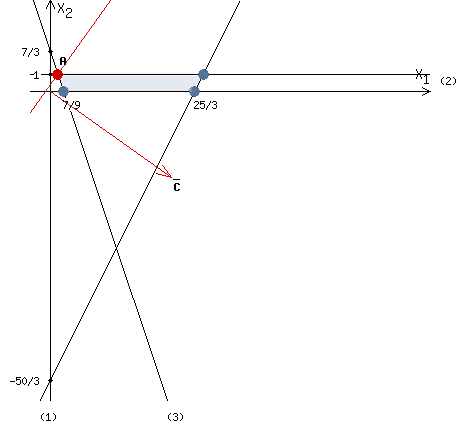Прямую 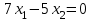будем двигать параллельно до первого касания с нашей областью ограничения. 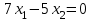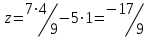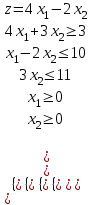В точке, в которой прямая в первый раз пересечет область допустимых решений, функция z достигает своего наименьшего значения.Функция z достигает наименьшего значения в точке A.Координаты точки A (4/9,1).Вычислим значение функции z в точке A (4/9,1):Решение:Найдем максимум функции. Решим задачу графически.Строим область ограничения функции и целевую функцию. 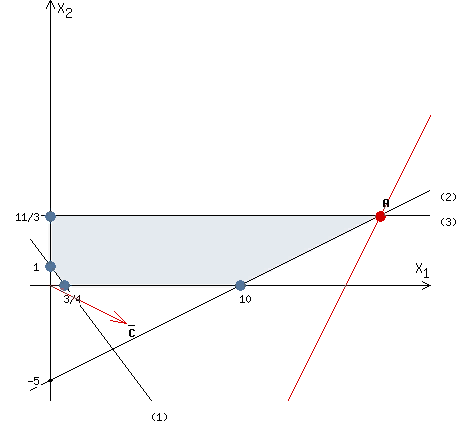Прямую 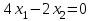будем двигать параллельно до последнего касания с нашей областью ограничения. В точке, в которой прямая

---

Смотрите также файлы

• Петровка, село Павловского района Воронежской области.doc

• Эссе по фильмам Три веселые смены и Завтрак на траве.docx

• 1. Решите неравенство. В ответе укажите номер правильного варианта. 1 2 3 4 2.docx

• Отчет по учебной ознакомительной практике студента 2 курса 062150 группы юи тгу иванова Ивана Ивановича.docx

• Вопрос 1 Субъекты Российской Федерации и муниципальные образования создавать региональные и муниципальные информационные системы в сфере закупок, при условии их интеграции с еис. Выберите один ответ обязаны вправе Правильный ответ вправе Вопрос 2.docx