Данные таблицы 3 позволяют построить гистограмму значений случайной величины (рис.1). Гистограмма – статистическая фигура, состоящая из прямоугольников с основанием в виде отрезков, соответствующие длинам интервалов и высотам, соответствующим частостям. Для построения гистограммы по оси абсцисс откладываются интервалы, по оси ординат – частоты в виде ступенек. Для построения полигона рассеивания в серединах классов откладываются ординаты, пропорциональные абсолютным частотам. Вершины ординат соединяют линиями. 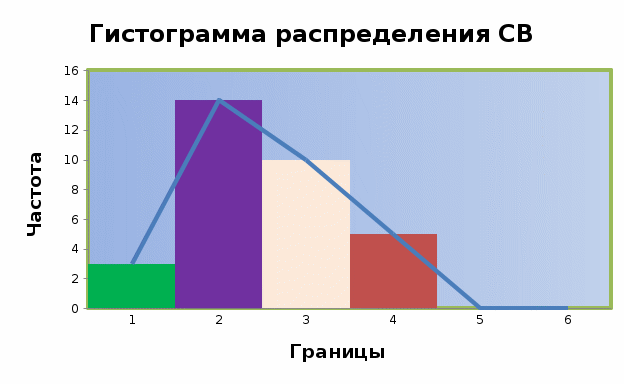Рисунок 1. Гистограмма распределения случайной величиныВыводВ процессе выполнения данной расчетно-графической работы были определены основные статистические оценки выборки, при анализе выборки была найдена дисперсия и среднеквадратичное отклонение. При обработке статистического материала я выявил наличие «выскакивающих значений» или грубых ошибок. Данные ошибки я выявил при помощи метода Шовене и правила «трёх сигм». После отбраковки грубых ошибок мною был произведен пересчет значений и составлена новая таблица с данными. Далее была произведена группировка данных, определен размах ряда, длина и число интервалов на основе этих данных составлена гистограмма и полигон. Данный график наглядно показал и подтвердил точность выше произведенных расчетов.

2. 
   Оценка значимости различия средних значений двух выборок.
   

В таблице представлены значения случайных величин первой и второй выборки:

№ опыта	Рейсовая скорость бурения, м/с	№ опыта	Рейсовая скорость бурения, м/с
1	10,5	1	14,0
2	12,0	2	14,5
3	12,5	3	10,0
4	13,0	4	3,7
5	15,0	5	12,0
6	8	6	12,5
7	11,0	7	16,0
8	12,0	8	18,0
9	13,5	9	20,5
10	9,5	10	17,0
11	7,0	11	32,0
12	13,0	12	15,0
13	13,5	13	16,0
14	11,5	14	19,0
15	12,5	15	20,0
16	10,5	16	14,0

---

1. 
   Оценка значимости различия средних значений двух выборок с использованием критерия Стьюдента
   

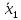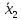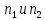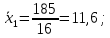
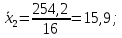
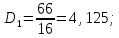
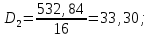
При обработке результатов наблюдений часто возникает необходимость в проверке гипотез относительно средних значений и двух независимых выборок . При этом применяется выборочная статистика.- Вычисляются средние значения выборок по формуле:Для первой выборки:Для второй выборки:- Вычисляются дисперсии выборок:Для первой выборки:Для второй выборки:Когда обе дисперсии неизвестны и не предполагается, что они равны, то есть 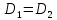равенство двух средних проверяют с помощью приближенного экспериментального коэффициента Стьюдента: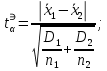где 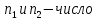наблюдений для первого и для второго опыта соответственно.- Расчетное значение критерия Стьюдента: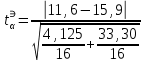=1,84 Табличное значение критерия Стьюдента при 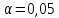, а число степеней свободы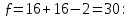 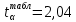Так как 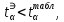то различие средних значений существенно, а значит, выборки не относятся к одной генеральной совокупности.

---

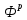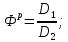
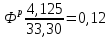
2.3 Оценка значимости различия средних значений двух выборок с использованием критерия Фишера.Распределение Фишера, называемое также Ф-распределением, для проверки гипотезы о равенстве дисперсий случайных величин. В качестве критерия Фишера служит отношение дисперсий, причем в числитель отношения всегда помещают большую дисперсию.- Рассчитываем экспериментальное значение критерия Фишера:- Вычисленное значение критерия сравнивается с табличным значением. 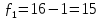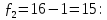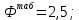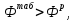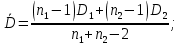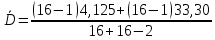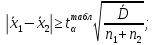Табличное значение критерия Фишера при и и Так как то расхождение дисперсий велико и различие средних значений существенно.- Вычисляется средневзвешенная дисперсия: =18,71- Табличное значение критерия Стьюдента при при , и - Выполняется проверка условия: 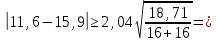1,564,3 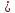1,56Так как условие выполняется, расхождение дисперсий велико и различие средних значений существенно.Вывод:Из табличных значений случайных величин первой и второй выборки была произведена оценка значимости различия средних значений двух выборок с использованием критерия Стьюдента и Фишера. Была выполнена проверка, которая соответствовала условию. Таким образом расхождение дисперсий велико и различие средних значений существенно.

---

Смотрите также файлы

• 4 тосан физика 10 сынып Электромагниттік индукция блімі бойынша жиынты баалау Тапсырмалар.docx

• 1 жргізуші айырлы кн, ардаты азаматтар, аяулы стаздар, білімге мар шкірттер! Кілдеріізге кктем шуаындай сезім мен нр йып, 7 мамыр Отан ораушылар мерекесі, 9 мамыр Жеіс кні мерекесі келіп жетті..docx

• Протокол от Председатель Уразбаева С. Б.docx

• Состояние ЗавершеныЗавершен Вторник, 17 января 2023, 22 42Прошло времени.pdf

• Конкурс педагогинноватор.pdf