Файл: Задача 1 качественный анализ работы подшипников коленчатого вала двс проверил Задорожная Е. А.docx
Добавлен: 05.12.2023
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
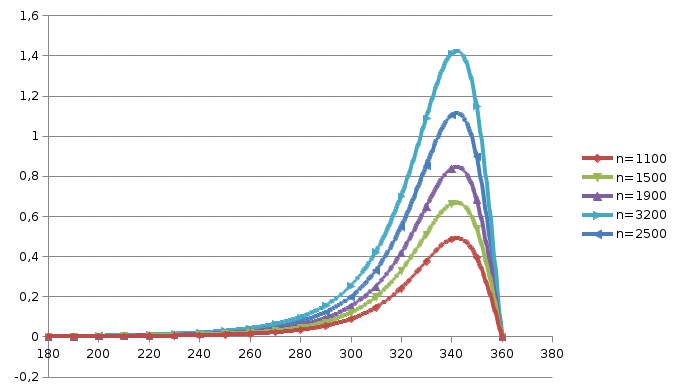
Рисунок 2 – Эпюры ГДД для статического нагружения (Е=0)
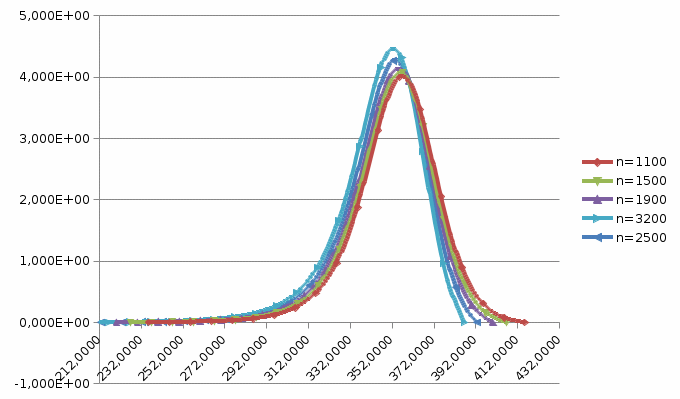
Рисунок 3 – Эпюры ГДД для динамического нагружения (Е=0,4)
Г. Используя табл. 1 и 2 совместно с рис. 2 и 3 определяем максимум П(φ) для каждого из заданных (n, E) и координату φmax. Рассчитать размерную величину давлений по формуле:
p = p* · П
Результаты расчета по формуле представлены в таблице 3.
Таблица 3 – Максимальные значения гидродинамических давлений
| E | n | max П(n) | ϕmax, град | max P, Па |
| 0 | 1100 | 0,485103 | 340 | 183881,7 |
| 1500 | 0,661504 | 340 | 250747,7 | |
| 1900 | 0,837905 | 340 | 317613,8 | |
| 2500 | 1,102506 | 340 | 417912,9 | |
| 3200 | 1,411208 | 340 | 534928,4 | |
| 0,4 | 1100 | 3,995947 | 358,9705 | 1514691,9 |
| 1500 | 4,068272 | 358,9705 | 1542107,1 | |
| 1900 | 3,944352 | 348,9705 | 1495134,6 | |
| 2500 | 4,265996 | 348,9705 | 1617055,9 | |
| 3200 | 4,317094 | 348,9705 | 1636425,0 |
Графические зависимости max П(n) для Е=0; E=0,4 представлены на рисунках 4 и 5.
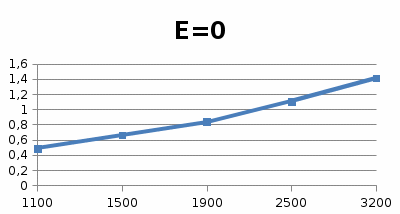
Рисунок 4 – Зависимость максимальных давлений от n, при Е=0
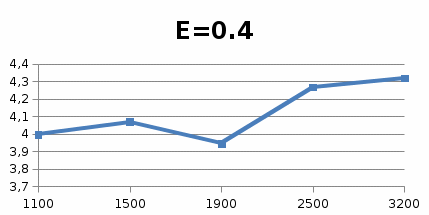
Рисунок 5 – Зависимость максимальных давлений от n, при Е=0,4
Д. Рассчитываем распределение гидродинамических давлений по осевой координате в середине несущей области
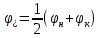 по формуле:
по формуле: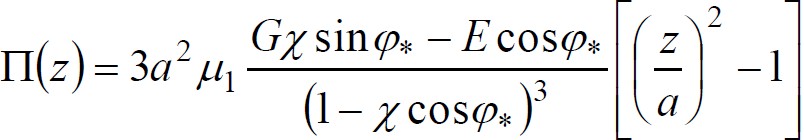
где α – безразмерная координата изменяется с шагом α /8, в пределах
-α ≤ z ≤ α.
Расчетные значения П(z) сводятся в таблицу 4
Таблица 4 – Распределение гидродинамических давлений в смазочном слое опоры по осевой координате в середине несущей области при Е=0 и при Е=0,4
| | E=0 | E=0,4 | |||||||||
| ϕ* | 270 | 270 | 270 | 270 | 270 | 325,491477 | 316,8476103 | 310,10091 | 302,6192 | 296,5650512 | |
| z n | 1100 | 1500 | 1900 | 2500 | 3200 | 1100 | 1500 | 1900 | 2500 | 3200 | |
| -0,17248 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| -0,15092 | 0,005086 | 0,006935 | 0,008784 | 0,011558115 | 0,014794387 | 0,22685437 | 0,253330741 | 0,2798071 | 0,319522 | 0,365855321 | |
| -0,12936 | 0,009493 | 0,012945 | 0,016397 | 0,021575148 | 0,027616189 | 0,42346149 | 0,472884049 | 0,5223066 | 0,59644 | 0,682929933 | |
| -0,1078 | 0,013222 | 0,018031 | 0,022839 | 0,030051099 | 0,038465407 | 0,58982136 | 0,658659926 | 0,7274985 | 0,830756 | 0,951223836 | |
| -0,08624 | 0,016274 | 0,022192 | 0,028109 | 0,036985968 | 0,047342039 | 0,72593398 | 0,81065837 | 0,8953828 | 1,022469 | 1,170737028 | |
| -0,06468 | 0,018647 | 0,025428 | 0,032209 | 0,042379755 | 0,054246086 | 0,83179935 | 0,928879382 | 1,0259594 | 1,171579 | 1,341469512 | |
| -0,04312 | 0,020342 | 0,027739 | 0,035137 | 0,04623246 | 0,059177549 | 0,90741747 | 1,013322962 | 1,1192285 | 1,278087 | 1,463421285 | |
| -0,02156 | 0,021359 | 0,029126 | 0,036894 | 0,048544083 | 0,062136426 | 0,95278835 | 1,063989111 | 1,1751899 | 1,341991 | 1,53659235 | |
| 0 | 0,021698 | 0,029589 | 0,037479 | 0,049314624 | 0,063122719 | 0,96791197 | 1,080877827 | 1,1938437 | 1,363292 | 1,560982705 | |
| ϕ*рад | 4,712389 | 4,712389 | 4,712389 | 4,71238898 | 4,71238898 | 5,68089796 | 5,530034026 | 5,4122819 | 5,281702 | 5,176036589 | |
Графики n (z) для каждого набора (n, E) представлены на рисунках 6 и 7:
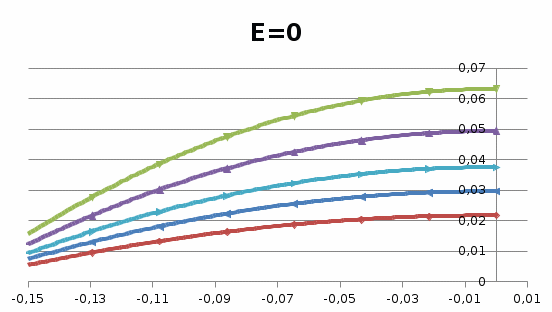

Рисунок 6 – Распределение гидродинамических давлений по ширине опоры (E=0)
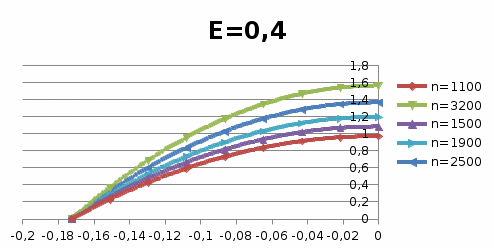
Рисунок 7 – Распределение гидродинамических давлений по ширине опоры (E=0,4)
Е. Рассчитать составляющие главного вектора сил гидродинамического давления в слое R(V , W) по формулам:
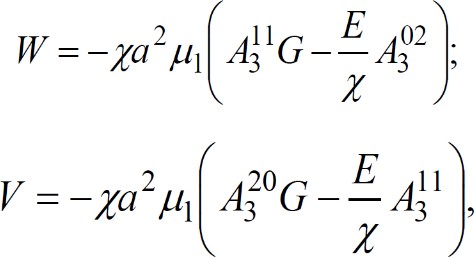
где значения интегральных функций:
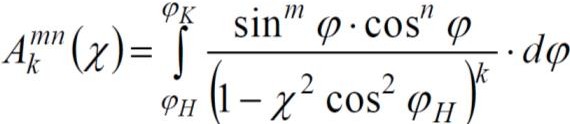
а для величин индексов k = 3; m = 0, 1, 2; n = 0, 1, 2; интегралы могут быть рассчитаны по следующим формулам:
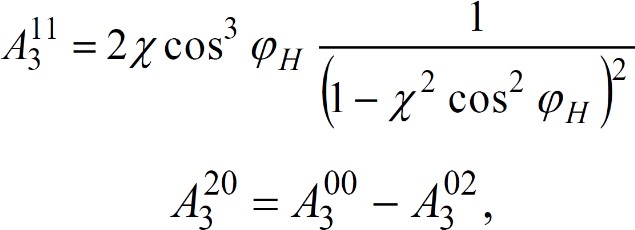
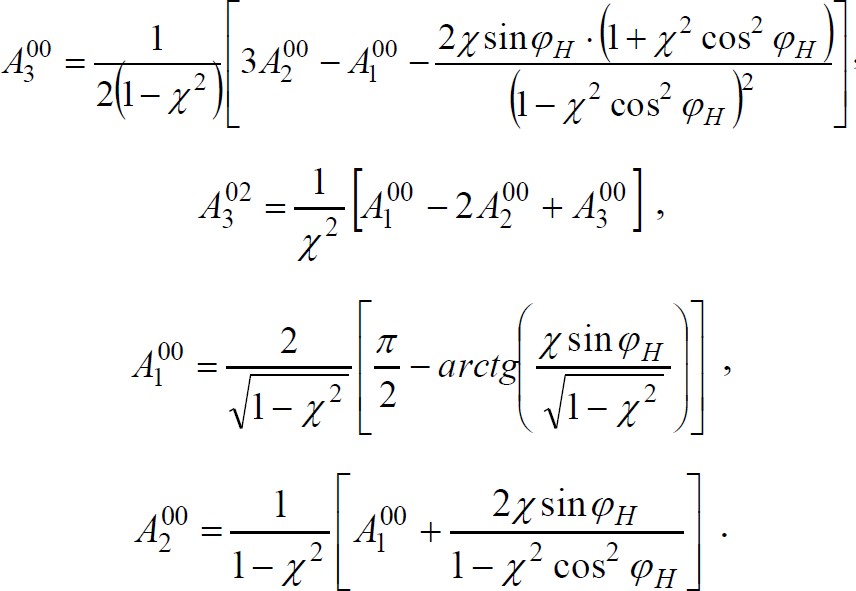 Таблица 6 – Значения интегралов и составляющих главного вектора сил гидродинамического давления
Таблица 6 – Значения интегралов и составляющих главного вектора сил гидродинамического давления| E | n | А311 | А100 | А200 | А300 | А302 | А320 | V | W |
| 0 | 1100 | -12,3457 | 5,235988 | 14,54441043 | 53,32950492 | 46,0572997 | 7,272205217 | -0,052598 | 0,089294 |
| 1500 | -0,071725 | 0,121765 | |||||||
| 1900 | -0,090852 | 0,154235 | |||||||
| 2500 | -0,119542 | 0,202941 | |||||||
| 3200 | -0,153014 | 0,259764 | |||||||
| 0,4 | 1100 | -0,46079 | 8,010664 | 17,64265757 | 65,16313358 | 59,2007538 | 5,962379752 | -0,047972 | 0,626152 |
| 1500 | -1,04281 | 7,807883 | 17,06070445 | 63,24865195 | 57,7111341 | 5,53751785 | -0,065587 | 0,617432 | |
| 1900 | -1,82995 | 7,601348 | 16,53831173 | 61,49733615 | 56,2844706 | 5,212865601 | -0,084376 | 0,615 | |
| 2500 | -3,20729 | 7,313293 | 15,92656427 | 59,39357457 | 54,4589673 | 4,934607263 | -0,114858 | 0,625655 | |
| 3200 | -4,80746 | 7,028265 | 15,44997551 | 57,69259399 | 52,8451691 | 4,847424865 | -0,152571 | 0,657108 |
Ж. Рассчитать коэффициент нагруженности опоры (число Зоммерфельда):
Определить значение характеристики режима работы опоры:
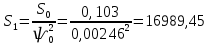
Рассчитать коэффициент перегрузки опоры:
kП= max П
S0
Оценить средние величины гидродинамических давлений в слое (Па) и несущей способности (Н):
Pср(B) = µ0 · ω0 · S1 = 0,0069 · 335,1 · 16989,45 = 39283,214 Па,
Rср(B) = Pср(B)BD2.
Восстановим модуль и направление внешней силы F, действующей на шип опоры. Для тяжело нагруженных опор коленчатого вала уравнение движения центра шипа записывается в виде уравнения баланса сил, так как инерционными силами, ввиду их малости по сравнению с внешними, пренебрегаем:
R(B)+F=0
Тогда:
F=-R(V+B)
Величину угла θ, определяющего положение линии центров относительно линии действия нагрузки, определяют по формуле:
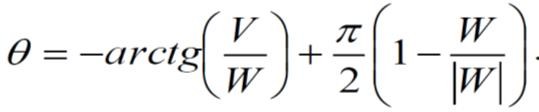
Результаты расчетов по приведенным формулам представлены в таблице 7 Таблица 7 – Результаты расчета основных силовых параметров опоры
| E | n | So | S1 | Pср, Па | R, H | θ, рад | kП | θ, град |
| 0 | 1100 | 0,10363 | 16989,45 | 39283,214 | 75,21361 | 0,53233 | 4,680922 | 30,5002 |
| 1500 | 0,14132 | 23167,43 | 53568,019 | 102,56401 | 0,53233 | 4,680922 | 30,5002 | |
| 1900 | 0,17900 | 29345,41 | 67852,824 | 129,91441 | 0,53233 | 4,680922 | 30,5002 | |
| 2500 | 0,23553 | 38612,39 | 89280,032 | 170,94001 | 0,53233 | 4,680922 | 30,5002 | |
| 3200 | 0,30148 | 49423,86 | 114278,440 | 218,80322 | 0,53233 | 4,680922 | 30,5002 | |
| 0,4 | 1100 | 0,62799 | 102950,2 | 238042,737 | 455,76853 | 0,07647 | 6,363109 | 4,3811 |
| 1500 | 0,62091 | 101789,5 | 235358,876 | 450,62987 | 0,10583 | 6,552152 | 6,0635 | |
| 1900 | 0,62076 | 101765,7 | 235303,791 | 450,52440 | 0,13635 | 6,354061 | 7,8121 | |
| 2500 | 0,63611 | 104282 | 241122,203 | 461,66463 | 0,18156 | 6,706375 | 10,4026 | |
| 3200 | 0,67459 | 110589,9 | 255707,420 | 489,59021 | 0,22814 | 6,399599 | 13,0716 |