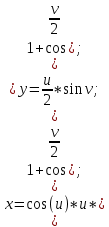ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 80
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича
Институт непрерывного образования
Лабораторные работы №1-№6 за 4 семестр
По дисциплине «Теория информации, данные, знания»
Вариант 2 (2010682)
Оглавление
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ 1
УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича 1
Лабораторные работы №1-№6 за 4 семестр 1
По дисциплине «Теория информации, данные, знания» 1
Введение 3
Лабораторная работа №1. «Массивы и матрицы в Scilab. Решение задач линейной алгебры» 4
Теоретический материал 4
Задание 1 5
Проверка задания 1 6
Задание 2 7
Выводы 9
Лабораторная работа №2. «Построение двумерных графиков» 10
Теоретический материал 10
Задание 1 11
задание 2 15
выводы 16
Лабораторная работа №3. «Построение трехмерных графиков» 17
Задание 1 17
задание 2 19
выводы 20
лабораторная работа №4. «Нелинейные уравнения и системы» 21
Задание 1 21
Задание 2 22
Выводы 23
Лабораторная работа №5. «Обработка экспериментальных данных» 24
Теоретическая часть 24
Задание 1 24
Решение 25
Задание 2 27
Решение 28
Выводы 29
Лабораторная работа №6. «Решение задач оптимизации» 31
Теория 31
задание 32
Решение 32
Введение
Scilab 1— пакет прикладных математических программ, предоставляющий открытое окружение для инженерных (технических) и научных расчётов. Это самая полная общедоступная альтернатива MATLAB.
Лабораторные работы позволят изучить на практике основные функции пакета программ, научиться использовать их в своих целях.
Лабораторная работа №1. «Массивы и матрицы в Scilab. Решение задач линейной алгебры»
Теоретический материал
Для работы с множеством данных удобно использовать массивы. Например, можно создать массив для хранения числовых или символьных данных. В этом случае вместо создания переменной для хранения каждого данного достаточно создать один массив, где каждому элементу будет присвоен порядковый номер. Таким образом, массив — множественный тип данных, состоящий из фиксированного числа элементов.
Как и любой другой переменной, массиву должно быть присвоено имя. Переменную, представляющую собой просто список данных, называют одномерным массивом, или вектором. Для доступа к данным, хранящимся в определенном элементе массива, необходимо указать имя массива и порядковый номер этого элемента, называемый индексом.
Если возникает необходимость хранения данных в виде таблиц, в формате строк и столбцов, то необходимо использовать двумерные массивы (матрицы). Для доступа к данным, хранящимся в таком массиве, необходимо указать имя массива и два индекса: первый должен соответствовать номеру строки, а второй — номеру столбца, в которых хранится необходимый элемент. Значение нижней границы индексации в Scilab равно единице. Индексы могут быть только целыми положительными числами.
Ввод элементов матрицы также осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а строки разделяются между собой точкой с запятой:
name=[x11, x12, ..., x1n; x21, x22, ..., x2n; ...; xm1, xm2, ..., xmn;]
Обратиться к элементу матрицы можно, указав после имени матрицы, в круглых скобках через запятую, номер строки и номер столбца на пересечении которых элемент расположен: name(индекс1, индекс2)
Для работы с матрицами и векторами в Scilab предусмотрены следующие операции:
-
+ — сложение;
-
- — вычитание1 ;
-
’ — транспонирование ;
-
— матричное умножение ;
-
— умножение на число;
-
ˆ — возведение в степень ;
-
\ — левое деление ;
-
/ — правое деление ;
-
.* — поэлементное умножение матриц;
-
.ˆ — поэлементное возведение в степень;
-
.\ — поэлементное левое деление;
-
./ — поэлементное правое деление
Для работы с матрицами и векторами в Scilab существуют специальные функции. Рассмотрим функции, которые понадобятся при выполнении данной работы.
-
det(M) — вычисляет определитель квадратной матрицы М;
-
inv(A) — вычисляет матрицу, обратную к A ;
-
insolve(A,b) — решает систему линейных алгебраических уравнений вида A ·
x −
b = 0.
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича
Институт непрерывного образования
Лабораторные работы №1-№6 за 4 семестр
По дисциплине «Теория информации, данные, знания»
Вариант 2 (2010682)
Оглавление
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ 1
УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича 1
Лабораторные работы №1-№6 за 4 семестр 1
По дисциплине «Теория информации, данные, знания» 1
Введение 3
Лабораторная работа №1. «Массивы и матрицы в Scilab. Решение задач линейной алгебры» 4
Теоретический материал 4
Задание 1 5
Проверка задания 1 6
Задание 2 7
Выводы 9
Лабораторная работа №2. «Построение двумерных графиков» 10
Теоретический материал 10
Задание 1 11
задание 2 15
выводы 16
Лабораторная работа №3. «Построение трехмерных графиков» 17
Задание 1 17
задание 2 19
выводы 20
лабораторная работа №4. «Нелинейные уравнения и системы» 21
Задание 1 21
Задание 2 22
Выводы 23
Лабораторная работа №5. «Обработка экспериментальных данных» 24
Теоретическая часть 24
Задание 1 24
Решение 25
Задание 2 27
Решение 28
Выводы 29
Лабораторная работа №6. «Решение задач оптимизации» 31
Теория 31
задание 32
Решение 32
Введение
Scilab 1— пакет прикладных математических программ, предоставляющий открытое окружение для инженерных (технических) и научных расчётов. Это самая полная общедоступная альтернатива MATLAB.
Лабораторные работы позволят изучить на практике основные функции пакета программ, научиться использовать их в своих целях.
Лабораторная работа №1. «Массивы и матрицы в Scilab. Решение задач линейной алгебры»
Теоретический материал
Для работы с множеством данных удобно использовать массивы. Например, можно создать массив для хранения числовых или символьных данных. В этом случае вместо создания переменной для хранения каждого данного достаточно создать один массив, где каждому элементу будет присвоен порядковый номер. Таким образом, массив — множественный тип данных, состоящий из фиксированного числа элементов.
Как и любой другой переменной, массиву должно быть присвоено имя. Переменную, представляющую собой просто список данных, называют одномерным массивом, или вектором. Для доступа к данным, хранящимся в определенном элементе массива, необходимо указать имя массива и порядковый номер этого элемента, называемый индексом.
Если возникает необходимость хранения данных в виде таблиц, в формате строк и столбцов, то необходимо использовать двумерные массивы (матрицы). Для доступа к данным, хранящимся в таком массиве, необходимо указать имя массива и два индекса: первый должен соответствовать номеру строки, а второй — номеру столбца, в которых хранится необходимый элемент. Значение нижней границы индексации в Scilab равно единице. Индексы могут быть только целыми положительными числами.
Ввод элементов матрицы также осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а строки разделяются между собой точкой с запятой:
name=[x11, x12, ..., x1n; x21, x22, ..., x2n; ...; xm1, xm2, ..., xmn;]
Обратиться к элементу матрицы можно, указав после имени матрицы, в круглых скобках через запятую, номер строки и номер столбца на пересечении которых элемент расположен: name(индекс1, индекс2)
Для работы с матрицами и векторами в Scilab предусмотрены следующие операции:
-
+ — сложение; -
- — вычитание1 ; -
’ — транспонирование ; -
— матричное умножение ; -
— умножение на число; -
ˆ — возведение в степень ; -
\ — левое деление ; -
/ — правое деление ; -
.* — поэлементное умножение матриц; -
.ˆ — поэлементное возведение в степень; -
.\ — поэлементное левое деление; -
./ — поэлементное правое деление
Для работы с матрицами и векторами в Scilab существуют специальные функции. Рассмотрим функции, которые понадобятся при выполнении данной работы.
-
det(M) — вычисляет определитель квадратной матрицы М; -
inv(A) — вычисляет матрицу, обратную к A ; -
insolve(A,b) — решает систему линейных алгебраических уравнений вида A ·
Задание 1
Решить систему линейных алгебраических уравнений, сделать проверку.
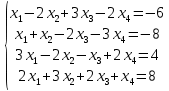
Для решения системы алгебраических уравнений с помощью матриц надо выполнить несколько шагов.
-
Записать систему уравнений в матричном виде -
Вычислить определитель матрицы -
Если определитель отличен от 0, то найти обратную матрицу -
Решить систему с помощью уравнения X = A-1*B
Выполним эти шаги. Записываем систему в матричном виде
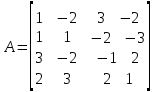 ,
, 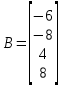 ,
, 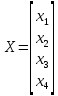
Вычисляем определитель матрицы.
В нашем случае матрица квадратная, для вычисления ее определителя можно использовать функцию Scilab «det(M)», которая вычисляет определитель квадратной матрицы.
Сначала зададим нашу матрицу в Scilab
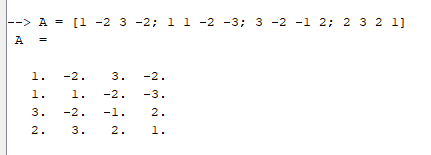
Рисунок 1. Задание матрицы A в scilab
Затем вычисляем определитель

Рисунок 2. Вычисление определителя матрицы в scilab
Определитель матрицы А = -288. Он не равен 0, поэтому надо найти обратную матрицу. Обратной матрицей по отношению к данной называется матрица того же типа, которая будучи умноженной как слева, так и справа на данную матрицу, в результате даст единичную матрицу.
В Scilab это можно сделать с помощью функции inv(A).

Рисунок 3. Нахождение обратной матрицы к а
Теперь есть все данные для вычисления системы уравнений. Умножаем обратную матрицу на матрицу В.
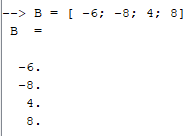
Рисунок 4. Задание матрицы В с Scilab

Рисунок 5.Умножение обратной матрицы к А на матрицу В
Ответ к системе уравнений.
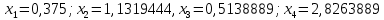
Проверка задания 1
Система уравнений решена. Для проверки мы можем перевести систему в систему уравнений вида A · x −b = 0.

И воспользуемся функцией linsolve(A,b).
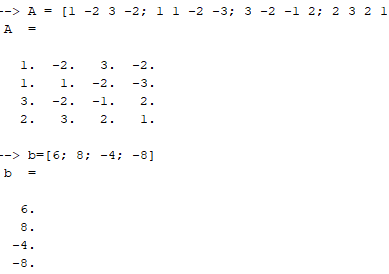
Рисунок 6. Задание матриц для решения системы

Рисунок 7. Решение системы уравнений

Проверка пройдена, система уравнений решена верно.
Задание 2
Если возможно, вычислить матрицу, обратную к матрице D.
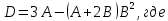
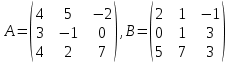
Сначала выполним все действия, необходимые для вычисления матрицы D.

Рисунок 8. Задание матриц а и в
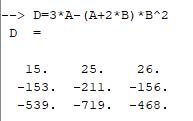
Рисунок 9. Вычисление матрицы d
Итогом вычисления стала матрица D
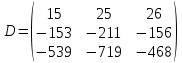
Обратная матрица существует только для квадратных матриц определитель которых не равен нулю. Вычислим определитель матрицы

Рисунок 10. Вычисление определителя матрицы D
Определитель отличен от нуля, значит, обратная матрица к D существует.

Рисунок 11.обратная матрица к D
Выводы
В данной работе мы рассмотрели основные действия с матрицами в Scilab, такие как задание матрицы, умножение, нахождение определителя, сложение, вычитание и возведение в квадрат.
Применили на практике 2 способа решения системы линейных алгебраических уравнений.
Лабораторная работа №2. «Построение двумерных графиков»
Теоретический материал
Рассмотрение графиков начнем с простейших функций вида y = f(x), для построения которых в Scilab существует функция plot. В предыдущих версиях Scilab (по третью версию Scilab включительно) функция plot предназначена для построения графика одной функции y = f(x). Обращение к ней имеет вид:
plot(x,y,[xcap,ycap,caption])
Здесь x — массив абсцисс; y — массив ординат; xcap, ycap, caption — подписи осей X, Y и графика соответственно.
При простейшем обращении к функции plot(x,y) создается окно с именем Scilab Graphic (0), в котором будет построен график функции y(x) на заданном интервале. Если же повторно обратиться к функции plot, будет создано новое графическое окно, и в нем будет построен новый график.
Для построения нескольких графиков в одной системе координат можно обратиться к функции plot следующим образом:
plot(x1,y1,x2,y2,...xn,yn)
где x1, y1 — массивы абсцисс и ординат первого графика; x2, y2 — массивы абсцисс и ординат второго графика; ... xn, yn — массивы абсцисс и ординат n-ого графика.
Следующей функцией, которая может быть использована для построения двумерных графиков, является функция plot2d.
В общем виде обращение к функции имеет вид:
plot2d([logflag],x,y’,[key1=value1,key2=value2,...,keyn=valuen]
где logflag — строка из двух символов, каждый из которых определяет тип осей (n — нормальная ось, l — логарифмическая ось), по умолчанию — «nn»; x — массив абсцисс; y — массив ординат или матрица, каждый столбец которых содержит массив ординат очередного графика — в случае, если необходимо построить графики нескольких функций y1, y2, ..., yn, когда все они зависят от одной и той же переменной x. При этом количество элементов в массиве x и y должно быть одинаковым. Если x и y — матрицы одного размера, то каждый столбец матрицы y отображается относительно соответствующего столбца матрицы x; keyi=valuei — последовательность значений свойств графика key1=value1, key2=value2, ..., keyn=valuen, определяющих его внешний вид. Возможные значения свойств графика будут подробно описаны ниже. Следует отметить, что вовсе не обязательно использовать полную форму записи функции plot2d со всеми ее параметрами. В простейшем случае к ней можно обратиться кратко, как и к функции plot.
Полярная система координат состоит из заданной фиксированной точки O — полюса, концентрических окружностей с центром в полюсе и лучей, выходящих из точки O, один из которых OX — полярная ось. Расположение любой точки M в полярных координатах можно задать положительным числом ρ = OM (полярный радиус), и числом ϕ, равным величине угла XOM (полярный угол). В Scilab для формирования графика в полярной системе координат необходимо сформировать массивы значений полярного угла и полярного радиуса, а затем обратиться к функции polarplot: polarplot(fi,ro,[key1=value1,key2=value2,...,keyn=valuen]), где fi — полярный угол; ro — полярный радиус;
keyn=valuen — последовательность значений свойств графика
Задание 1
Изобразите график функции
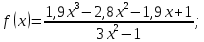
График функции можно построить с помощью функции plot.
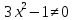 , поэтому построим графики в нескольких пределах.
, поэтому построим графики в нескольких пределах. [-5, -1], [-0.5, 0.5] и [1, 5]

Рисунок 12. задаем параметры графика
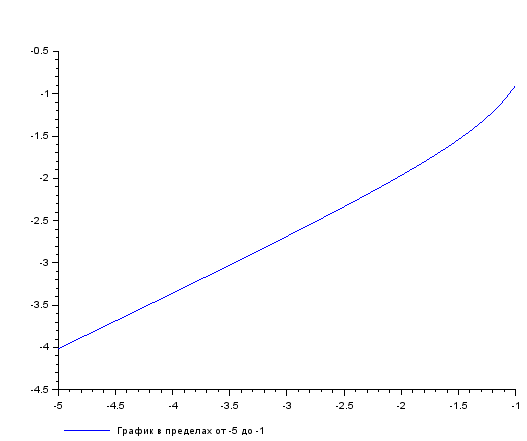
Рисунок 13.результат

Рисунок 14. задаем параметры графика
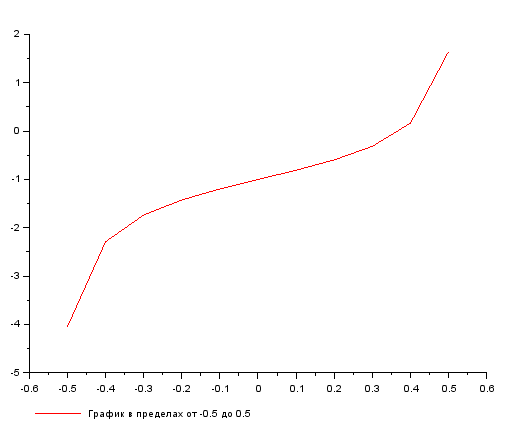
Рисунок 15. результат

Рисунок 16. ЗАДАЕМ ПАРАМЕТРЫ ГРАФИКА
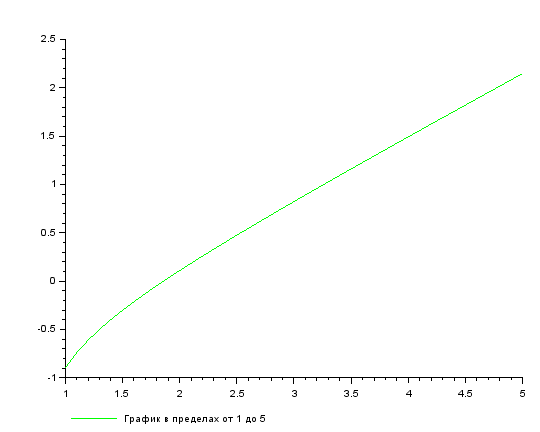
Рисунок 17. Результат
Выведем все на одном графике

Рисунок 18. параметры графика
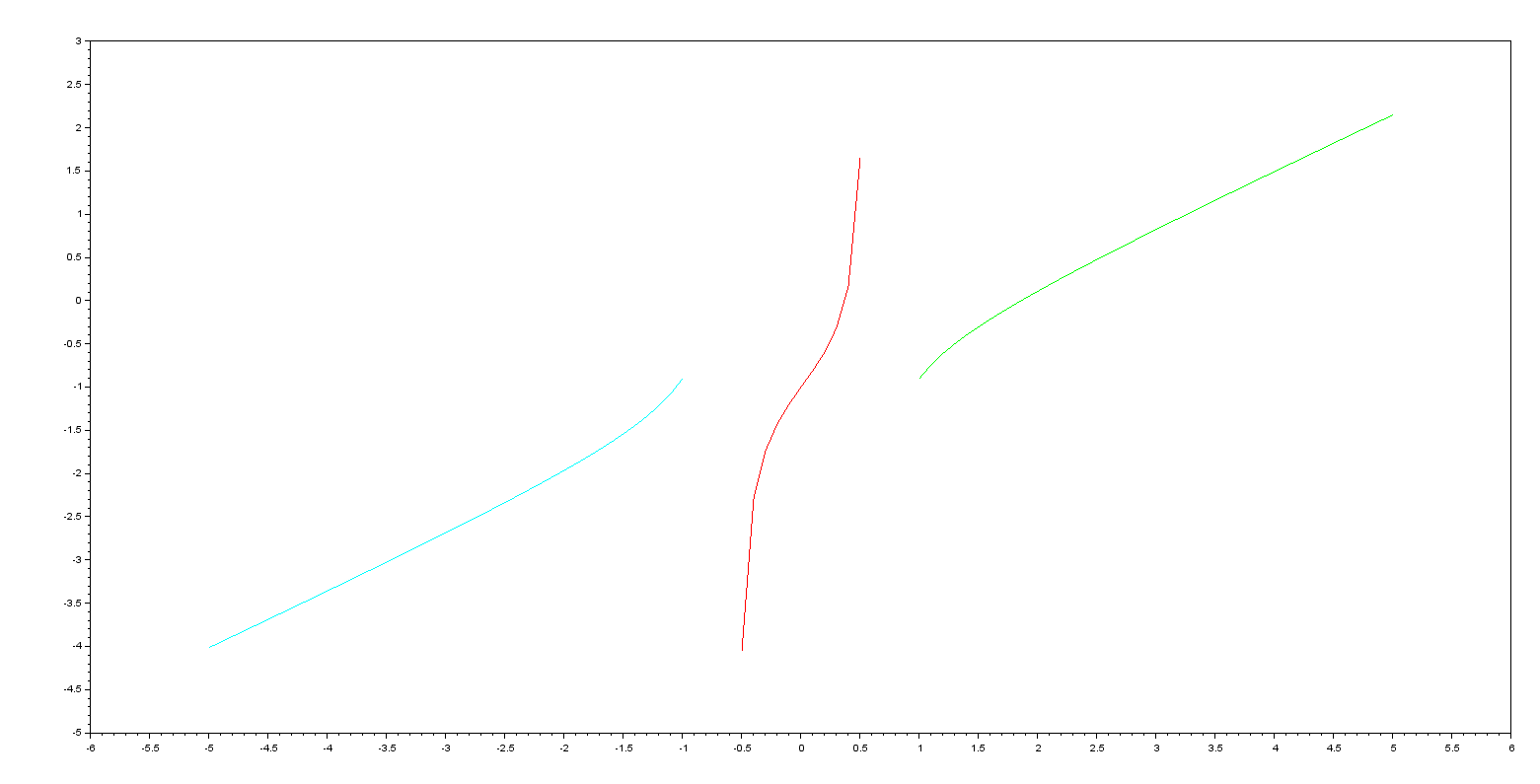
Рисунок 19. результат
задание 2
Изобразите график функции в полярных координатах
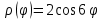

Рисунок 20. параметры функции
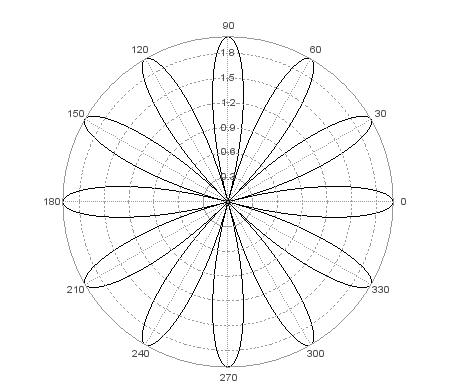
Рисунок 21. результат
выводы
При выполнении данной работы мы научились строить двумерные графики, графики в полярных координатах. Настраивать вывод графика, и располагать несколько графиков на одной координатной оси
Лабораторная работа №3. «Построение трехмерных графиков»
Задание 1
Построить график, заданный системой уравнений