Файл: Санктпетербургский государственный.docx

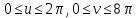
Сначала задаем массивы значений для параметров u и v



Затем вычисляем значения функций с данными значениями



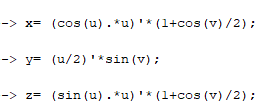
И строим график на основании полученных значений





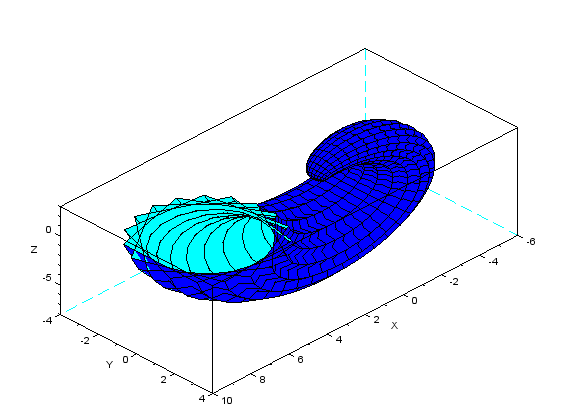
Рисунок 22.Результат

задание 2

Изобразить линии, заданные параметрически, где t [ ]

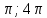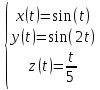и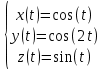

Задаем параметры для функции param3d и строим с ее помощью график



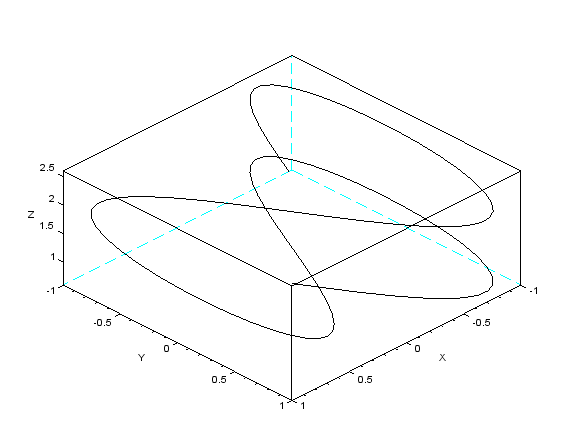
Задаем параметры для функции param3d и строим с ее помощью график

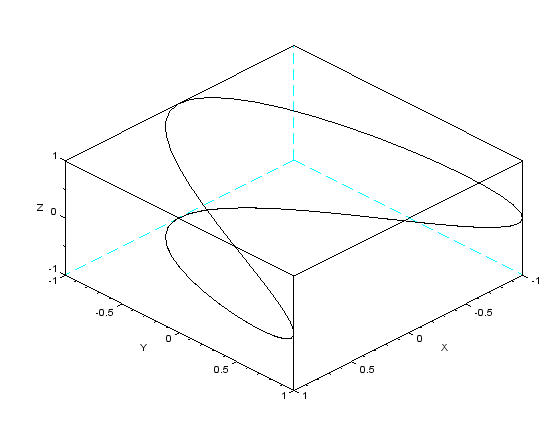
выводы

При выполнении данной работы мы научились строить 3D поверхности в Scilab и линии, заданные параметрически. Рассмотрели функции, позволяющие создавать 3d графики.

лабораторная работа №4. «Нелинейные уравнения и системы»

Задание 1

Найти корни полиномов.







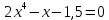
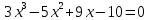
Сначала задаем полином, предварительно определив вектор коэффициентов



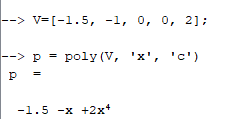
Затем находим корни



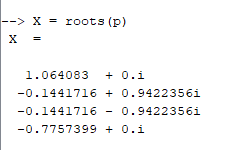
Корни второго полинома найдем аналогично

---

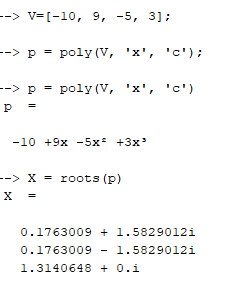
Задание 2

Решить систему уравнений



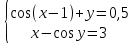
Для решения системы уравнений надо сначала задать пользовательскую фукнцию, затем, с помощью fsolve с различными значениями получить ответ.

Выводы

При выполнении данной работы мы научились решать системы уравнений в scilab и находить корни полиномов.

Лабораторная работа №5. «Обработка экспериментальных данных»

Теоретическая часть

Метод наименьших квадратов позволяет по экспериментальным данным подобрать такую аналитическую функцию, которая проходит настолько близко к экспериментальным точкам, насколько это возможно.

Пусть в результате эксперимента были получены некоторые данные, отображенные в виде таблицы (табл. 11.1). Требуется построить аналитическую зависимость, наиболее точно описывающую результаты эксперимента

Идея метода наименьших квадратов заключается в том, что функцию Y = f(x, a0, a1, . . . , ak) необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений yi от расчетных Yi была наименьшей: 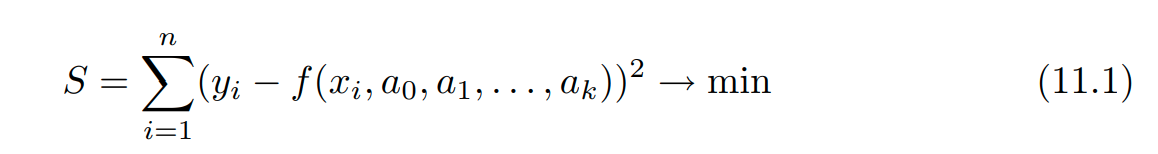Задача сводится к определению коэффициентов ai из условия (11.1). Для реализации этой задачи в Scilab предусмотрена функция

[a,S]=datafit(F,z,с)

где F — функция, параметры которой необходимо подобрать; z — матрица исходных данных; c — вектор начальных приближений; a — вектор коэффициентов; S — сумма квадратов отклонений измеренных значений от расчетных.

Задание 1

В результате эксперимента была определена некоторая табличная зависимость. С помощью метода наименьших квадратов определить линию регрессии, рассчитать коэффициент корреляции, подобрать функциональную зависимость заданного вида, вычислить коэффициент регрессии. Определить суммарную ошибку.

Решение

Сначала задаем пользовательскую функцию



И задав так же массивы экспериментальных данных, формируем матрицу исходных данных и указываем вектор начальных приближений

---

Находим вектора коэффициентов (a) и сумму квадратов отклонений измеренных от расчётных (S), она же суммарная ошибка



Строим графики экспериментальных данных и функциональной зависимости:





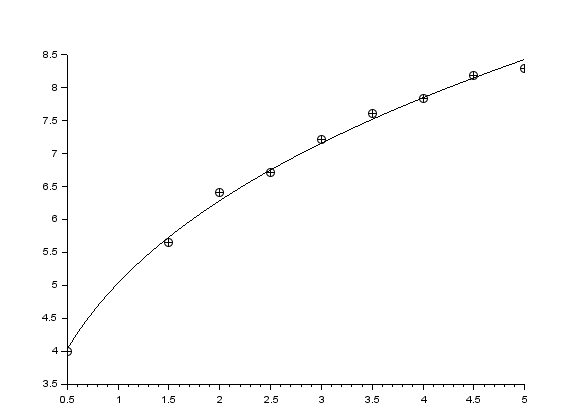
Находим коэффициенты регрессии и добавляем линию регрессии на график

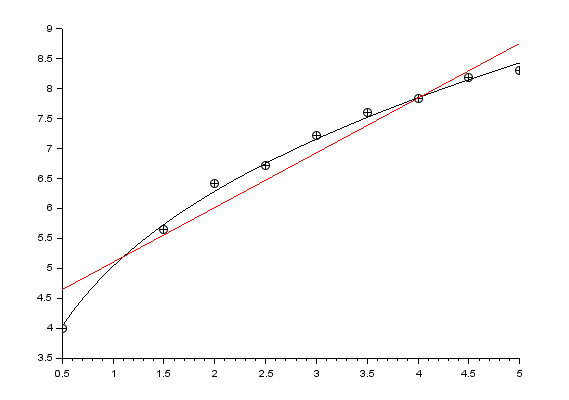Находим коэффициент корреляции r и индекс корреляции R

Задание 2

Задание 5.2. Для вариантов 1-7 найти приближенное значение функции при заданном значении аргумента с помощью функции линейной интерполяции. Функция задана таблично.

Решение

Задаем массивы значений



Создаем график регрессии





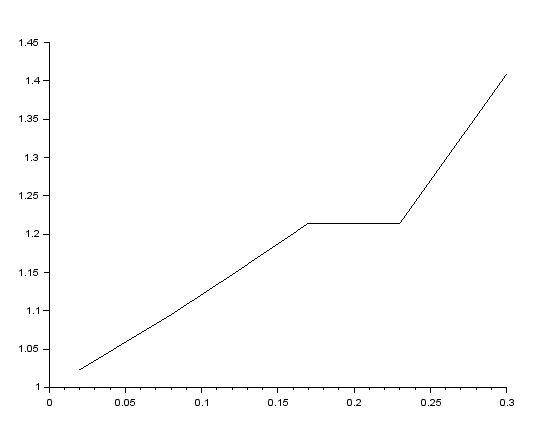
Задаем массив значения х в заданных точках



Создаем матрицу исходных данных, и, применив функцию линейной интерполяции, наносим точки на график

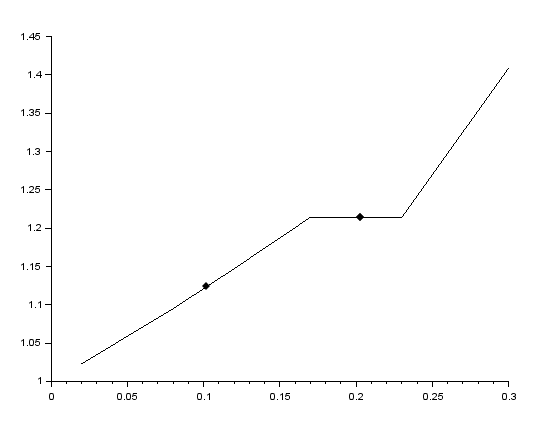
Выводы

С помощью Scilab можно обработать экспериментальные данные, использовать метод наименьших квадратов и выводить результаты в графическом виде.

Лабораторная работа №6. «Решение задач оптимизации»

---

Теория

При нахождении минимума функции многих переменных функцию costf необходимо построить таким образом, чтобы входными данными в нее были значения вектора неизвестных x и параметра ind. Функция costf должна зависеть не от нескольких неизвестных, а от одного массива (вектора) неизвестных. В случае функции многих переменных структура функции сostf должна быть такой:



Для решения задач линейного программирования в Scilab предназначена функция linpro следующей структуры:

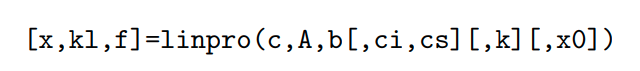Здесь c — массив (вектор-столбец) коэффициентов при неизвестных функции цели, длина вектора n совпадает с количеством неизвестных x.

A — матрица при неизвестных из левой части системы ограничений, количество строк матрицы равно количеству ограничений m, а количество столбцов совпадает с количеством неизвестных n.

b — массив (вектор-столбец), содержит свободные члены системы ограничений, длина вектора m.

ci — массив (вектор-столбец) размерности n содержит нижнюю границу переменных (cij 6 xj ); если таковая отсутствует, указывают [].

cs — массив (вектор-столбец) длиной n, содержит верхнюю границу переменных (csj > xj ); если таковая отсутствует, указывают [].

k — целочисленная переменная, используется, если в систему ограничений кроме неравенств входят и равенства, в матрице они будут находиться в k первых строках, оставшиеся l строк займут неравенства, т.е. m = k + l.

x0 — вектор-столбец начальных приближений длиной n.

Функция linpro возвращает массив неизвестных x, минимальное значение функции f и массив множителей Лагранжа kl.

задание

Решить задачу целочисленного программирования

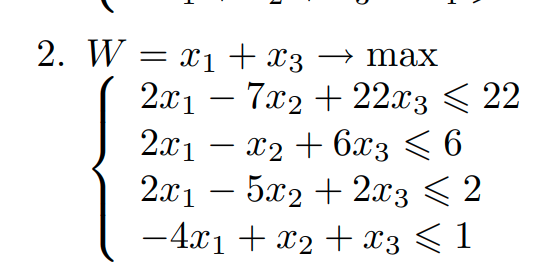
Решение

Сначала задаем известные нам из системы данные: массив коэффициентов функции цели (с), матрицу при неизвестных левой части неравенства (А) и массив, который содержит свободные члены системы ограничений(b).

Затем задаём массив (вектор-столбец), который содержит нижнюю границу переменных и применяем функцию linpro

---

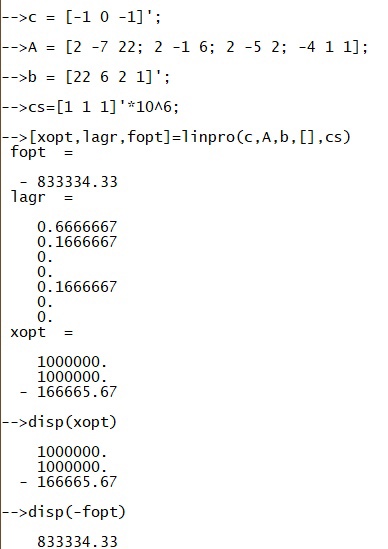
Рисунок 23. решение и результат кода

---