Файл: Подтема 01 Числовая последовательность, способы её задания и свойства Конспект.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 118

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Подтема 01: Числовая последовательность, способы её задания и свойства

  1. Конспект
Определение: Функцию y = f(x), x N, называют функцией натурального аргумента или числовой последовательностью и обозначают y = f(n) или , , ,…, ,… – первый член последовательности, - второй член последовательности, - третий член последовательности, - n-ый член последовательности,n - индекс, который задает порядковый номерПоследовательностью называется бесконечное множество пронумерованных элементов.Числовая последовательность – это частный случай функции. Как и любая функция, последовательность может задаваться различными способами.Способы задания числовой последовательности:1. Аналитический (при помощи формулы)2. Словесный3. РекуррентныйI. Аналитический способ задания числовой последовательностиПоследовательность задана аналитически, если указана формула для вычисления ее n -го члена. ,

где

Пример № 1. Рассмотрим функцию

График состоит из отдельных точек









…



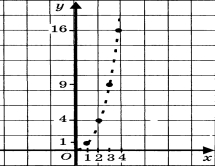
Получим последовательность чисел

1, 4, 9, 16, 25, …, , … Последовательность квадратов натуральных чисел

Пример № 2.

Найти первый, третий и шестой члены последовательности

Ответ:

Пример № 3. Задать последовательность формулой n-го члена:

а) 2, 4, 6, 8, … б) 4, 8, 12, 16, 20, …

Ответ: а) б)

II. Словесное задание числовой последовательности.

Правило составления последовательности описывается словами

Пример № 1:

последовательность простых чисел

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …

последовательность кубов натуральных чисел

1, 8, 27, 64, 125, …

III. Рекуррентное задание числовой последовательности.

Указывается правило позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены.

При вычислении членов последовательности по этому правилу мы все время возвращаемся назад, выясняем чему равны предыдущие члены, поэтому такой способ называют рекуррентным ( от латинского recurrere – возвращаться)Пример 1:y1=3, yn= yn-1 + 4, если n = 2, 3, 4, …Каждый член последовательности получается из предыдущего прибавлением к нему числа 4y1 = 3 y2 = y1 + 4= 3 + 4 = 7y3= y2+ 4= 7 + 4 = 11 y4 = y3 + 4= 11 + 4 = 15 и т.д.Получаем последовательность 3, 7, 11, 15, 19, 23, 27, …Пример 2:y1=1, y2=1, yn= yn-2 + yn-1Каждый член последовательности равен сумме двух предыдущих членовy1=1 y2=1 y3= y1 + y2 = 1 + 1 = 2y4 = y2 + y3= 1 + 2 = 3 y5 = y3 + y4 = 2 + 3 = 5 и т.д.Получаем последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …Монотонные последовательностиПоследовательность (уn ) – возрастающая, если каждый ее член (кроме первого) больше предыдущего, т.е. у1 < у2 < у3 < у4 < … < уn < … Пример: 2, 4, 6, 8, 10, …Если а > 1, то последовательность уn = аn– возрастает.Последовательность (уn ) – убывающая, если каждый ее член (кроме первого) меньше предыдущего, т.е. у1 > у2 > у3 > у4 > … > уn > … Пример: -1, -3, -5, -7, -9, …Если 0 < а < 1, то последовательность уn = аn– убывает.Возрастающие и убывающие последовательности называются монотонными.Последовательности, которые не возрастают и не убывают, являются
немонотонными.2. Ссылка на урок:https://www.youtube.com/watch?v=aHyVQ9h8moA 3. Задания1. По заданной формуле n-го члена вычисли первые три члена последовательности.А)


C) D) E) ## tema:24 level:a answer: e ptema:01chet:2 napr:1||2. Укажи номер члена последовательности , равного .A) 4B) 6C) 8D) 9E) 10## tema:24 level:b answer:b ptema:01chet:2 napr:1||3. Найди наименьший член последовательности и укажи его номер:A) n=2, B) n=2, C) n=3, D) n=1, E) n=4, ## tema:24 level:a answer: a ptema:01chet:2 napr:1||4. По данной формуле числовой последовательности определить четвёртый член последовательности.A) 12B) 81C) 27D)243 E) 33 ## tema:24 level:a answer: b ptema:01chet:2 napr:1||5. Определите правило составления числовой последовательности: 1; 4; 7; 10; 13; … Задайте формулой общий член этой последовательности. A)

=2n+1

B) =3n-2
C) =2n+2
D)
E)
## tema:24 level:a answer: b ptema:01chet:2 napr:1||

6. Определи математическую модель следующей задачи.

Поднялся сильный ветер и стал срывать листья с дерева со скоростью 9 листьев в мин. Сколько листьев ветер сорвёт с дерева через 9 минут с момента начала сильного ветра?

A) ) y=9x,x∈Z ; 81 листьев
B) y=9x, x∈N; 90 листьев
C) ) y=9x,x∈Z; 80 листьев
D) y=9x, x∈N; 84 листьев
E) y=9x, x∈N; 81 листьев
## tema:24 level:b answer: e ptema:01chet:2 napr:1||

7. Дано: =-1; =3. Найдите третий член числовой последовательности, заданной рекуррентной формулой: = .

A)
B)
C)
D)
E)
## tema:24 level:b answer: d ptema:01chet:2 napr:1||

Смотрите также файлы