Вид центра зависит от назначения сети и характера грунта. Официальными нормативными документами [16, 17, 21] установлены типовые конструкции центров, зависящие от класса пункта и местных условий. Они различны для районов сезонного промерзания грунтов, для районов многолетней мерзлоты, для районов распространения подвижных песков.

На рис. 6.3 показан центр пункта государственной геодезической сети 1 - 4 классов для районов сезонного промерзания грунта. Центр представляет собой железобетонный пилон сечением  см и скрепленный с ним цементным раствором якорь диаметром 50 см и высотой 20 см. Основание центра располагают на 50 см ниже границы наибольшего промерзания грунта, но во всех случаях не менее 1,5 м от поверхности земли. На верху пилона крепится (цементным раствором или приваривается) чугунная марка, на верхней поверхности которой отмечена точка, к которой относятся координаты пункта.

В 1,5 м устанавливают способствующий отысканию центра опознавательный знак – железобетонный столб с укрепленной на нем металлической охранной плитой, обращенной в сторону центра.

До внедрения в геодезическое производство спутниковых технологий над центрами геодезических пунктов устанавливались наружные геодезические знаки  деревянные или металлические сооружения, служащие объектом визирования на пункт и для подъема геодезических приборов над землей. Основными типами наружных знаков являлись пирамида и сигнал (рис. 6.4).

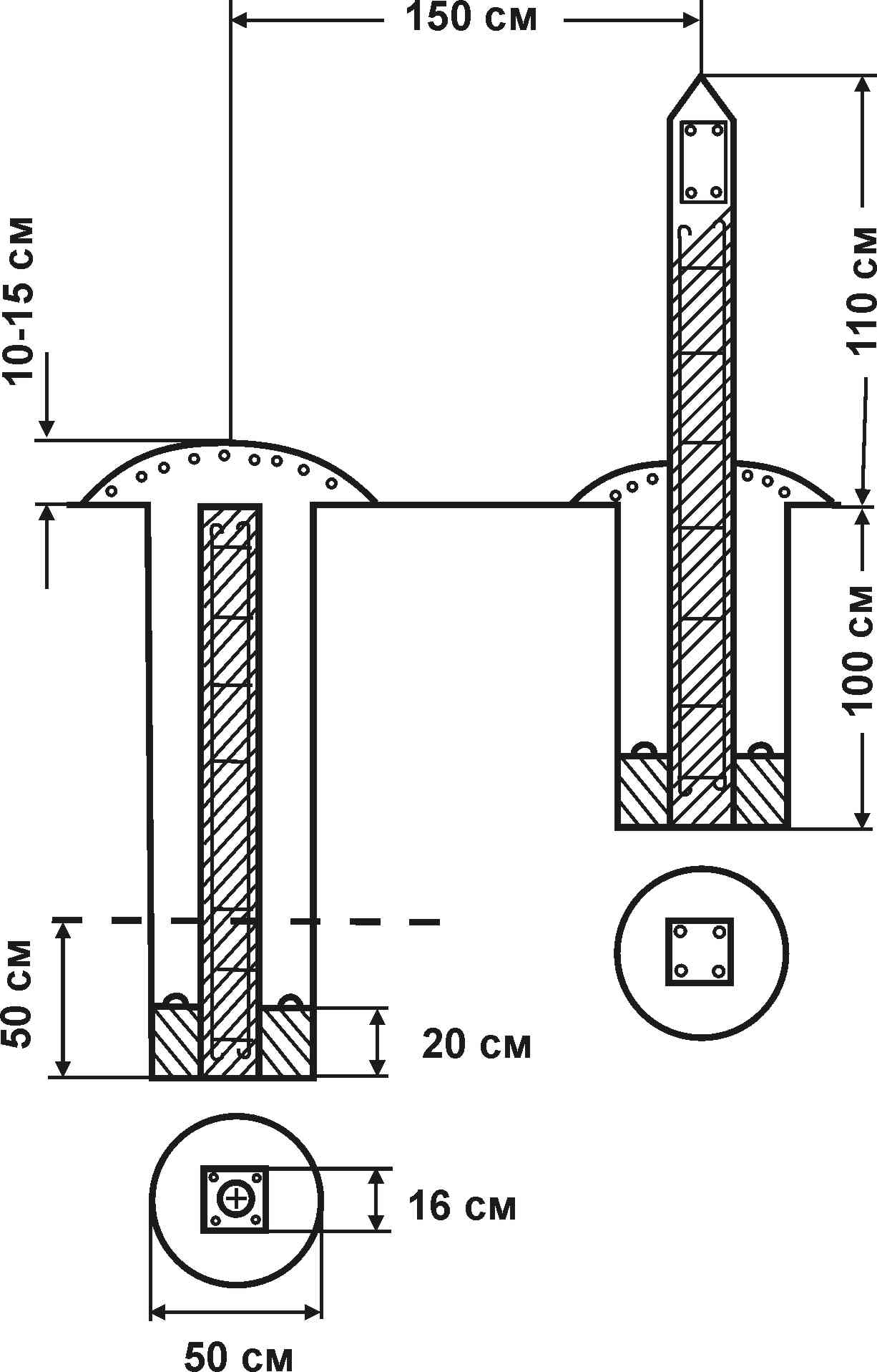Рис. 6.3. Центр геодезического пункта: - - - - -  граница промерзания грунта	Рис. 6.4. Геодезические знаки: слева – пирамида; справа – сигнал

6.4. Создание съемочных сетей проложением теодолитных ходов

Теодолитные ходы. Теодолитным ходом называют ход полигонометрии, выполненный методами, достаточными для обеспечения точности, требуемой в съемочных сетях.

---

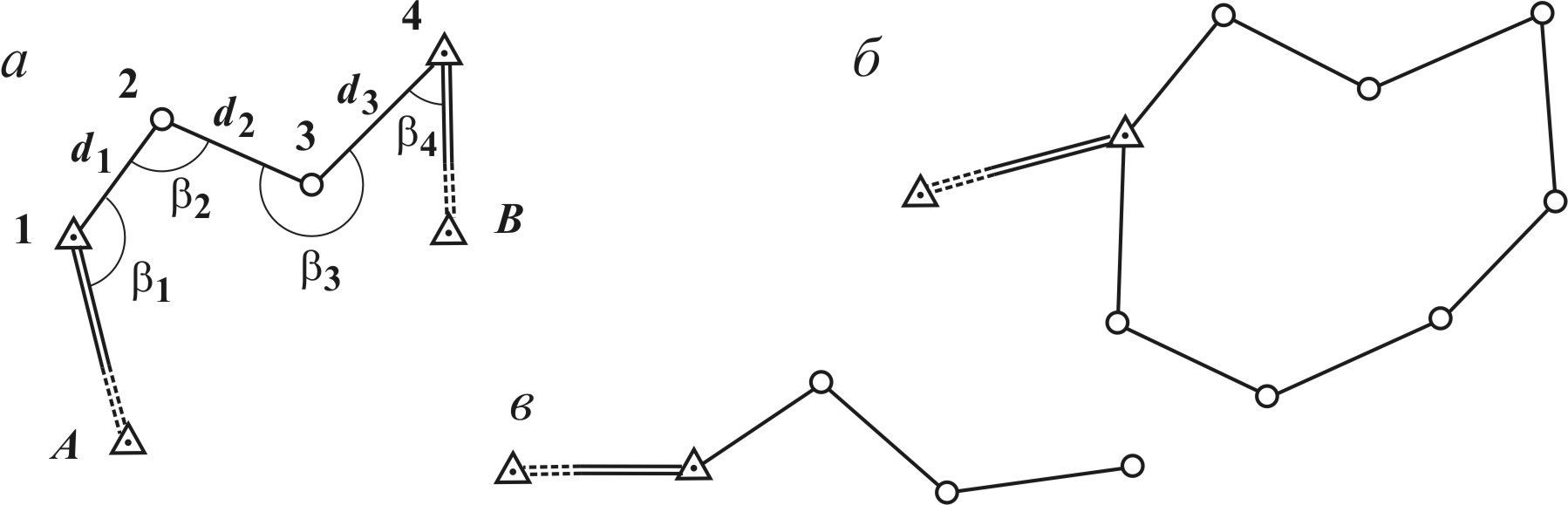
Рис. 6.5. Схемы теодолитных ходов: а – разомкнутого; б – замкнутого; в– висячего.

По форме теодолитный ход может быть разомкнутым  опирающимся на два исходных пункта и два исходных направления (рис. 6.5 а); замкнутым  опирающимся на один исходный пункт и одно направление (рис. 6.5 б); висячим  разомкнутым ходом, опирающимся на один исходный пункт и одно направление (рис. 6.5 в). Теодолитные ходы могут образовать систему теодолитных ходов с узловыми точками в местах их соединения (см. рис. 6.2 б).

Проект съемочной сети составляют на топографической карте или плане. Но часто положение ходов выбирают непосредственно на местности в процессе рекогносцировки. При этом учитывают ограничения на длину хода между исходными пунктами, приведенные в табл. 6.2. Длины ходов, опирающихся на узловые точки, уменьшают на 30%.

Таблица 6.2

Масштаб съемки	Открытая местность, застроенная территория			Закрытая местность
	Допустимые относительные невязки
	13000	12000	11000	12000	11000
	Допустимая длина теодолитного хода, км
1:5000 1:2000 1:1000 1:500	6,0 3,0 1,8 0,9	4,0 2,0 1,2 0,6	2,0 1,0 0,6 0,3	6,0 3,6 1,5 -	3,0 1,5 1,5 -

Места для точек хода выбирают так, чтобы обеспечить взаимную видимость между ними, благоприятные условия для съемки окружающей местности, удобства установки геодезических приборов и сохранность точек.

Точки ходов закрепляют деревянными кольями, костылями, металлическими трубами и т.п. Часть точек закрепляют знаками долговременной сохранности  столбами, бетонными монолитами.

Углы поворота теодолитного хода измеряют электронным тахеометром или теодолитом. При этом следят, чтобы на всех точках хода измерялись только правые, или только левые по ходу углы.

Для измерения угла в его вершине устанавливают прибор, а в соседних точках – визирные цели. Угол измеряют одним приемом.

Длины сторон измеряют электронным тахеометром или светодальномером, а при их отсутствии – землемерной лентой.

Результаты измерения углов и расстояний записывают в журналы установленной формы. При выполнении измерений тахеометром запись результатов измерений выполняется автоматически  в памяти прибора, откуда в последующем они вводятся для обработки в компьютер.

---

Обработка разомкнутого теодолитного хода. Исходными данными

в разомкнутом ходе (рис. 6.5 а) являются координаты начального и конечного пунктов 1 и 4 ( ,  , ,  ) и дирекционные углы начального A-1 и конечного 4-Bнаправлений ( и ).

При обработке вручную записи ведут в ведомость установленной формы (табл. 6.3). В графу 1 вписывают названия или номера точек. Вписывают исходные данные: в соответствующие строки графы 3  начальный и конечный дирекционные углы, а в графы 7 и 8 – координаты начального и конечного пунктов (исходные данные в таблице выделены жирным шрифтом). Вписывают результаты измерений: измеренные углы – в графу 2, горизонтальные проложения сторон хода – в графу 4.

Уравнивание углов. Подсчитывают сумму измеренных углов . Теоретически эта сумма должна быть равна:

для правых углов  ;

для левых углов  ,

где n  число измеренных углов. В табл. 6.3 углы  правые.

Отличие фактической суммы углов от теоретической представляет угловую невязку хода:

. (6.2)
Таблица 6.3

Ведомость вычисления координат точек теодолитного хода

Названия точек	Измеренные углы	Дирекционные углы		Длины сторон, м	Приращения координат, м		Координаты, м
							x	y
1	2	3		4	5	6	7	8
A
	0,3	349º 50,0′
I	113º 26,0′				0,03	+0,04	6322,70	4057,25
	0,3	56 24,3		138,56	+76,67	+115,42
II	85 07,5				0,03	+0,03	6399,34	4172,71
	0,3	151 17,1		116,30	102,00	+55,88
III	211 44,5				0,04	+0,05	6297,31	4228,62
	0,3	119 32,9		197,24	97,27	+171,59
IV	56 33,2						6200,00	4400,26
		243 00,0
B
 = 46651,2′		P = d = 452,10			x = = 122,60	y = = +342,89
			= 122,70; = 343,01;
= 4180 			м
			= + 342,89  343,01 =  0,12 м
			м

---

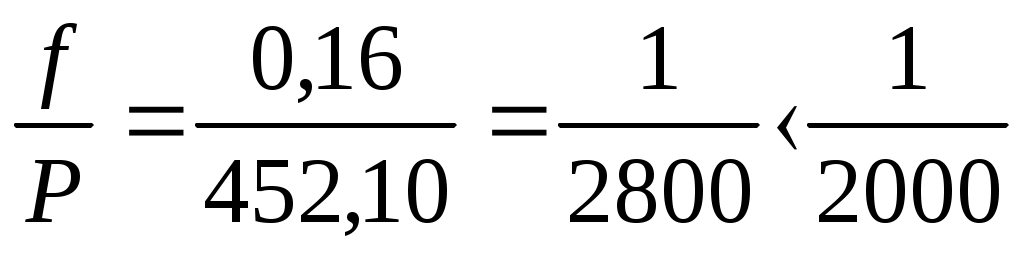Вычисленную угловую невязку сравнивают с допустимой

.

Если угловая невязка меньше допустимой, что указывает на доброкачественность угловых измерений и правильность вычислений, то невязку распределяют поровну во все измеренные углы со знаком, противоположным знаку невязки. Полученные при этом поправки



вписывают над измеренными углами в графу 2. Невязка редко делится на число углов без остатка. Поэтому поправки округляют, вводя большие в углы с более короткими сторонами. При этом сумма поправок должна равняться невязке с обратным знаком: _ = f_.

Вычисление дирекционных углов. Дирекционные углы вычисляют, используя начальный дирекционный угол и измеренные углы _i, исправленные поправками _, по формулам:

для правых углов  ;

для левых углов  .

Здесь индексы i= 1, 2, …, n соответствуют номерам углов и сторон на рис. 6.5 а, причем ₀ = _нач и _n = _кон.

Контролем правильности вычислений служит равенство вычисленного и заданного значений конечного дирекционного угла.

Вычисление приращений координат выполняют по дирекционным углам и длинам сторон хода (графы 5 и 6).

; (i= 1, 2, …, n1).

Вычислив суммы приращения абсцисс и ординат , находят координатные невязки

, . (6.3)

Вычисляют абсолютную невязку

---

и относительную невязку ходаfP,где  длина хода. Если относительная невязка не превосходит допустимой (обычно, 12000), то невязки f_xи f_y распределяют (см. записи курсивом в графах 5 и 6), в виде поправок к приращениям координат,пропорциональных длинам сторон, и со знаками, противоположными знакам невязок:

; . (6.4)

Суммы поправок должны равняться невязкам с обратным знаком:

; .

Если из-за выполненных округлений равенства нарушаются, поправки, вычисленные по формулам (6.4), несколько изменяют, добиваясь соблюдения равенств.

Вычисление координат точек теодолитного хода выполняют по формулам (см. графы 7 и 8)

; (i = 1, 2, …, n1).

Контролем правильности вычислений служит совпадение вычисленных и заданных координат последней точки теодолитного хода.

Обработка замкнутого теодолитного хода.

Последовательность обработки замкнутого хода такая же как и разомкнутого. Но исходными в замкнутом теодолитном ходе служат координаты одного из пунктов хода и дирекционный угол одной из сторон. Это накладывает на обработку замкнутого хода следующие особенности.

Угловая невязка вычисляется по формуле (6.2), в которой в отличие от разомкнутого хода

,

где n – число углов в полигоне.

После распределения угловой невязки и вычисления дирекционных углов сторон хода контролируют правильность вычислений  в конце должно быть получено то же значение дирекционного угла, которое было исходным.

Невязки в координатах находят по формулам:

,

---

Смотрите также файлы

• Создание и редактирование документа в текстовом редакторе.doc

• Реферат Проблема здоровьесбережения в условиях современной дошкольной образовательной организации студент группы 2Е.docx

• Экзаменационные билеты для проверки знаний по программе Оказание первой помощи пострадавшим.docx

• Личностного развития.pptx

• Слайд 3 Сегодня система наставничества в школе.docx