Файл: Федеральное государственное бюджетное образовательное учреждение высшего образования братский государственный университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 54
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«БРАТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Кафедра «Машиноведения, механики и инженерной графики»
Теория механизмов и машин
Курсовой проект
Механическая ножовка
23.05.01.ТММ.01.КП.00.00.00.ПЗ
Выполнил:
ст. группы ТТС-19 Дмитриев М.Н.
Проверил:
Ст.преподаватель Кобзова И.О.
Братск 2021
 СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
Задание.....................................................................................................................3
Введение..................................................................................................................4
1. Структурный анализ рычажного механизма..............................................5
2. Кинематический анализ механизма..............................................................8
2.1 План положений......................................................................................8
2.2 План скоростей........................................................................................9
2.3 План ускорений.....................................................................................12
2.4 Построение диаграмм...........................................................................14
3. Силовой расчёт механизма............................................................................15
3.1. Определение сил инерции, моментов пар сил инерции и сил тяжести звеньев..........................................................................................................15
3.2. Определение реакций в кинематических парах................................16
3.3. Силовой расчёт начального звена......................................................18
3.4. Рычаг Н.Е. Жуковского.......................................................................19
4. Синтез зубчатых механизмов........................................................................21
4.1. Расчет основных геометрических параметров зубчатой передачи.......21
4.2. Построение эвольвентного зацепления....................................................25
Заключение...........................................................................................................27
Список используемой литературы...................................................................28
З АДАНИЕ
АДАНИЕ
| Параметр | Обозначение | Единица | Вариант числовых значений |
| 1 | |||
| Длинна кривошипа | Loa | м | 0,05 |
| Длинна шатуна | Lab | м | 0,2 |
| Число оборотов кривошипа | n1 | Об\мин | 140 |
| Масса кривошипа | m1 | Кг | 3 |
| Масса шатуна | m2 | Кг | 8 |
| Масса ползуна | m3 | Кг | 10 |
| Сила сопротивления | F3c | кН | 1,0 |
| Момент инерции шатуна | Js2 | Кг*м2 | 0,03 |
| Коэффициент неравномерности хода | b | - | 0,07 |
| Число оборотов электродвигателя | Nдв | Об\мин | 1800 |
| Число зубьев | Z4 | - | 11 |
| Z5 | - | 32 | |
| Модуль зацепления | m | Мм | 4,0 |
| Положение кривошипа при силовом расчете механизма | Φ1 | Град | 45 |
ВВЕДЕНИЕ
Механическая ножовка предназначена для отрезки круглого и профильного материала из стали, чугуна и цветных металлов.
Выходным звеном механизма является ползун, несущий на себе пилу. Основной исполнительный механизм, служащий для приведения ползуна в возвратно-поступательное движение, представляет собой рычажный механизм.
Движение кривошип исполнительного механизма получает от электродвигателя через коробку скоростей, имеющую планетарную и не-планетарную ступени.
При поступательном движении ползуна на рабочем ходу пила, на холостом ходу – возвращается в исходное положение.

-
 СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНОГО
СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНОГО
МЕХАНИЗМА
Структурный анализ кривошипно-ползунного механизма сводится к решению двух задач:
1) определению подвижности механизма;
2) определению состава структуры.
Рассмотрим каждую задачу в отдельности.
Подвижность кривошипно-ползунного механизма определяется по структурной формуле Чебышева:
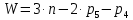 ,
,где p4, p5 – количество кинематических пар четвертого и пятого классов, n – количество подвижных звеньев кинематической цепи.
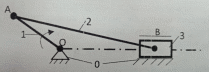
Рис. 1.1. Схема кривошипно-ползунного механизма
Структурная схема рассматриваемого механизма состоит из четырех звеньев (рис. 1.1):
1 – звено ОА – кривошип
2 – звено АВ – шатун,
3 – звено В – ползун,
0 – стойка.
При этом звенья 1–3 являются подвижными звеньями, а стойка 0 – неподвижным звеном. Следовательно, n = 3.
 Для определения значений коэффициентов p4 и p5 выявим все кинематические пары, входящие в состав схемы механизма. Результаты анализа заносим в табл. 1.
Для определения значений коэффициентов p4 и p5 выявим все кинематические пары, входящие в состав схемы механизма. Результаты анализа заносим в табл. 1.Таблица 1
| п/п | Номера звеньев/ название | Схема | Класс |
| 1 |
|  | 5 |
| 2 | 1-2 / вращательная | 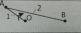 | 5 |
| 3 | 2-3 / вращательная |  | 5 |
| 4 | 3-0 / поступательная |  | 5 |
Из анализа данных табл. 1 следует, что p5 = _4_, а p4 = _0_.
Подставив найденные значения коэффициентов в структурную формулу Чебышева, получим
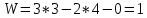
Результат показывает, скольким звеньям необходимо сообщить независимые движения, чтобы получить определенность движения всех остальных его звеньев.
Состав структуры кривошипно-ползунного механизма исследуем согласно принципу построения механизмов по Ассуру.
Группа звеньев 2-3 представлена на рис. 1.2,а.
n = _2_; p5 = _3_, p4 = _0_.
Подставив выявленные значения коэффициентов в структурную формулу Чебышева, получим
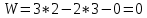
Следовательно, группа звеньев 3 – 2 является структурной группой 2-го класса 2-го порядка 2-го вида, структурная формула которой имеет вид ВВП.
Группа звеньев 0–1 представлена на рис. 1.2, б.
n =_1_, p5 = _1_, а p4 = _0_.
 Подставив выявленные значения коэффициентов в структурную формулу Чебышева, получим
Подставив выявленные значения коэффициентов в структурную формулу Чебышева, получим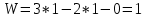
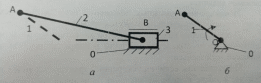
Рис. 1.2. Состав структуры по Ассуру.
Следовательно, группа звеньев 0–1 не является структурной группой, а представляет собой первичный механизм.
Из проведенного структурного анализа следует, что структура кривошипно-ползунного механизма состоит из первичного механизма с подвижностью, равной 1, и одной структурной группы 2-го класса 2-го порядка 2-го вида.
 2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМАОсновными задачами кинематического исследования механизмов являются:
1) выявление возможных положений всех звеньев механизма за рассматриваемый промежуток времени;
2) определение величин скоростей характерных точек механизма, а также выявление значений и направлений угловых скоростей всех звеньев;
3) определение величин ускорений характерных точек механизма, а также выявление значений и направлений угловых ускорений всех звеньев.
2.1. Определение положения звеньев механизма
с помощью построения плана положений
Выбираем масштабный коэффициент планов механизма с таким расчётом, чтобы планы положений механизма заняли примерно 1/5 часть площади листа формата А1:
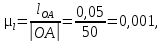 (2.1)
(2.1)где |ОА| – произвольный отрезок от 25 до 50 мм.
В соответствии с выбранным масштабным коэффициентом находим длину шатуна АВ.
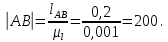 (2.2)
(2.2)Построение планов положений начинают с изображения элементов стойки, т. е. шарнирно-неподвижных опор и направляющих.
За начальное принимаем крайнее положение выходного звена (ползуна). Под крайним положением подразумевают такие положения выходных звеньев, в которых оси кривошипа и шатуна окажутся на одной прямой.
Для определения перемещения поршня в зависимости от положения кривошипа от точки В0 отложить максимальный ход
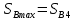 поршня.
поршня.Построить на чертеже длины хода поршня от начальной точки В0 (В8):
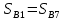 ;
;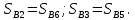
Действительная длина хода поршня в метрах при вращении кривошипа вычисляется по формуле:
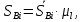
 где
где 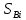 – перемещение поршня механизма на чертеже в i–м положении, мм, при i = 1, 2, 3, 4, 5, 6, 7 и 8.
– перемещение поршня механизма на чертеже в i–м положении, мм, при i = 1, 2, 3, 4, 5, 6, 7 и 8.Полученные значения перемещения поршня (точки В) заносятся в табл.2.1.
Таблица 2.1
Перемещение поршня в зависимости
от положения кривошипа
| Положение механизма | 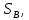 мм мм | 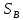 , м , м |
| А0 | 0 | 0 |
| А1 | 17 | 0,017 |
| А2 | 57 | 0,057 |
| А3 | 88 | 0,088 |
| А4 | 100 | 0,1 |
2.2. Построение плана скоростей
По заданной частоте вращения определим угловую скорость кривошипа, с-1, по формуле:
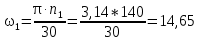 , (2.3)
, (2.3)где
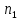
– число оборотов кривошипа в минуту.
Скорость точки Aопределяется векторной суммой:
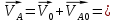 , (2.4)
, (2.4)где
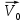 – вектор скорости точки О. Точка О является неподвижной точкой, следовательно, значение скорости этой точки равно нулю, т. е.
– вектор скорости точки О. Точка О является неподвижной точкой, следовательно, значение скорости этой точки равно нулю, т. е. 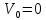 ;
;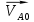 – вектор относительной скорости точки A вокруг неподвижной точки O.
– вектор относительной скорости точки A вокруг неподвижной точки O.Определим скорость относительного вращательного движения точки A вокруг неподвижной точки O

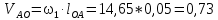 (2.5)
(2.5)где
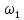 – угловая скорость кривошипа 1;
– угловая скорость кривошипа 1; 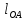 – длина кривошипа 1.
– длина кривошипа 1.Вектор скорости точки B, принадлежащей шатуну 2, определяется суммой:
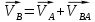 , (2.6)
, (2.6)здесь
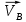 – неизвестный по величине вектор абсолютной скорости точки В;
– неизвестный по величине вектор абсолютной скорости точки В;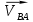 – вектор относительной скорости точки В вокруг условно неподвижные точки А.
– вектор относительной скорости точки В вокруг условно неподвижные точки А.В то же время точка B принадлежит и ползуну 3. Ползун 3 может совершать только возвратно-поступательное движение параллельно прямой ОВ. Следовательно, линия действия вектора скорости точки В, принадлежащей ползуну 3, всегда параллельна прямой ОВ:
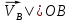 .(2.7)
.(2.7)Совместное решение выражений (2.6) и (2.7) позволит определить направление и линию действия вектора скорости точки B.
Масштабный коэффициент плана скоростей
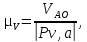
где |Pv,a| − произвольный отрезок, изображающий на плане скоростей вектор скорости относительного вращательного движения точки A вокруг точки O.
Принимаем |Pv,a| от 50 до 100 мм.
Разрешив графически векторные уравнения (2.4), (2.6), (2.7), построим план скоростей.
Замерим на плане скоростей длины отрезков | Pv,b|,
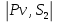 и |ab|, мм.
и |ab|, мм.