Определим значения соответствующих скоростей.

Скорость точки B, м/с:
.
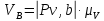Скорость относительного вращательного движения точки B вокруг точки А, м/с:

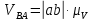. (2.8)
Скорость центра масс шатуна, м/с:
.
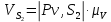Определим значения и направления действия угловых скоростей звеньев механизма.

Угловая скорость шатуна 2 с учетом формулы (2.8), c^-1:
.
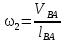Полученные значения заносим в таблицу 2.2.

Таблица 2.2

Результаты расчёта кинематических параметров

механизма

Положение механизма	Отрезки на плане скоростей (мм)			Скорости точек (м/с)				Угловая скорость ( c-1)
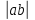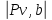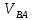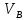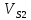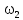0	70	0	35	0,7	0	0,35	3,5
1	51	59	60	0,51	0,59	0,6	2,55
2	0	70	0	0	0,7	0	0
3	59	40	50	0,59	0,4	0,5	2,95
4	70	0	35	0,7	0	0,35	3,5
5	51	40	50	0,51	0,4	0,5	2,55
6	0	70	0	0	0,7	0	0
7	52	60	60	0,52	0,6	0,6	2,6
8	70	0	35	0,7	0	0,35	3,5
9	52	60	60	0,52	0,6	0,6	2,6

---

Ползун 3 совершает только поступательные движения, следовательно, угловая скорость этого звена равна нулю, т. е. ω₃ = 0.

2.3. Построение плана ускорений
Для построения плана ускорений составим векторные уравнения.

Ускорение точки А определяется векторной суммой:
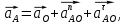(2.9)
где 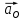– вектор ускорения точки О, имеет значение, равное нулю, т. е. ;

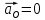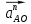– вектор нормального (центростремительного) ускорения .

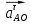– вектор тангенциального (вращательного) ускорения, его значение равно нулю, т. к. по условию задачи угловая скорость кривошипа является постоянной величиной.

Так как кривошип вращается равномерно (n₁=const), значит, нормальное (центростремительное) ускорение, м/с²:
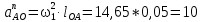,73. (2.10)
Ускорение точки B, принадлежащей шатуну 2, определяется векторной суммой:
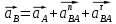, (2.11)
здесь 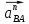– вектор нормального (центростремительного) ускорения.

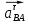– вектор тангенциального (вращательного) ускорения.

Следовательно, нормальное (центростремительное) ускорение с учетом формулы (2.8), м/с²:
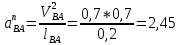. (2.12)
В то же время точка B принадлежит и ползуну 3. Ползун 3 совершает только прямолинейное возвратно-поступательное движение вдоль направляющей (прямая OB), следовательно, линия действия вектора ускорения точки B проходит параллельно прямой OB: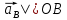
. (2.13)
Масштабный коэффициент плана ускорений, м/с²·мм:

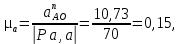
где | 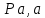| − произвольный отрезок, изображающий на плане ускорений вектор нормального ускорения движения точки

---

A вокруг точки O. Принимаем 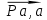от 50 до 100 мм

Длина отрезка, изображающего в составе плана вектор нормального ускорения с учетом формулы (2.10), мм: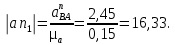

Разрешив графически векторные уравнения (2.9), (2.11), (2.13), построим план ускорений.

Замерив на плане ускорений длины соответствующих отрезков, определим значения ускорений, м/с²:


;

;


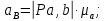
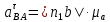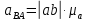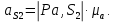
Определим значения и направления угловых ускорений.

Известно, что кривошип 1 вращается с постоянной угловой скоростью и значение вектора тангенциального (касательного) ускорения равно нулю, следовательно, угловое ускорение данного звена также равно нулю, с-2:



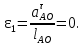
Угловое ускорение шатуна 2, с^-2:





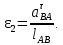
Полученные значения заносим в таблицу 2.3.


2.4. Построение диаграмм
Используя полученные результаты вычислений из таблиц 2.1, 2.2 и 2.3 для всех положений механизма построим диаграммы движения ползуна механизма.

По оси абсцисс откладываем угол φ, а по оси ординат – перемещение поршня 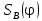, скорости 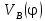и ускорения 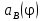точки В механизма.

Масштабный коэффициент по оси угла поворота кривошипа:




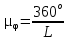, град/мм,
где 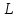– длина абсциссы на чертеже.

Таблица 2.3

Результаты расчёта кинематических параметров механизма

Положение механизма	Отрезки на плане ускорений (мм)					Ускорения точек (м/с2)					Угловые ускорения звеньев (c-1)
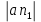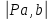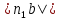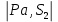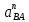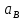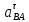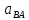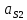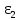0 (8)	16	87	0	70	78	2,45	13,05	0	10,5	11,7	65,25
1	9	47	44	51	54	1,3	7,05	6,6	7,65	8,1	35,25
2	0	20	74	0	37	0	3	11,1	0	5,55	15
3	11	45	48	59	52	1,7	6,75	7,2	8,85	7,8	33,75
4	16	54	0	70	62	2,45	8,1	0	10,5	9,3	40,5
5	9	48	50	51	55	1,3	7,2	7,5	7,65	8,25	36
6	0	20	73	0	37	0	3	10,95	0	5,55	15
7	9	46	48	52	54	1,4	6,9	7,2	7,8	8,1	34,5
9	9	46	48	52	54	1,4	6,9	7,2	7,8	8,1	34,5

3. СИЛОВОЙ РАСЧЁТ МЕХАНИЗМА
Целью силового расчёта является определение усилий, действующих на звенья механизма (внешние силы), реакций в кинематических парах (внутренние силы), определение уравновешивающего момента, приложенного к начальному механизму. Решение такой задачи необходимо для последующих расчётов машины на прочность, жесткость, вибростойкость. При расчёте рассматриваем указанное в задании расчётное положение механизма.

3.1. Определение сил инерции, моментов пар

сил инерции и сил тяжести звеньев
1. Силы инерции шатуна 2 и ползуна 3 найдем согласно формулам, H:



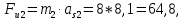
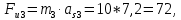
где m₂, m₃ − соответственно массы 2-го и 3-го звеньев;

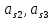− ускорение центра масс 2-го и 3-го звеньев.

Вектор ускорения центра масс ползуна 3 совпадает с вектором ускорения точки В, тогда м/с².

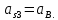
Вектора сил инерци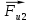и и 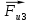лежат на прямых параллельных, соответственно, линиям действия векторов ускорений центров масс 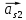и 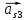, а направление действия этих векторов противоположно направлению действия векторов ускорений центров масс этих звеньев.

2. Момент пары сил инерции вычисляется по формуле
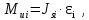(3.1)
здесь J_Si − момент инерции i-го звена;

ε_i− угловое ускорение i-го звена.

Угловая скорость кривошипа 1 является постоянной величиной, следовательно, угловое ускорение этого звена равно нулю, т. е. ε₁ = 0, тогда согласно формуле (3.1) имеем, H⋅м:



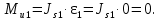
Ползун 3 совершает только поступательные движения, следовательно, угловое ускорение этого звена равно нулю, т. е ε₃ = 0, тогда согласно формуле (3.1) найдем момент пары сил инерции ползуна 3, H⋅м: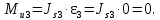

Момент пары сил инерции шатуна 2 найдем согласно формуле

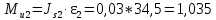. (3.2)
Направление действия момента пары сил инерции 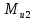противоположно направлению действия углового ускорения ε₂. Следовательно, момент пары сил инерции шатуна 2 действует в направлении хода часовой стрелки (рис. 3.1, а).

3. Силы тяжести звеньев вычисляем по формулам, Н





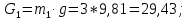
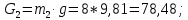
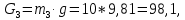
где 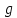– ускорение свободного падения; 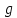= 9,81 м/с²;

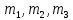– массы звеньев 1, 2 и 3.


3.2. Определение реакций в кинематических парах
Для определения реакций в кинематических парах отсоединяем от механизма ведущее звено 1 и стойку.

Оставшаяся кинематическая цепь представляет собой нулевую группу, состоящую из звеньев 2 и 3.

Вычерчиваем в выбранном масштабе план группы 2 – 3 в заданном положении.

В соответствующие точки прикладываем все внешние силы ( ).

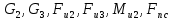Силы инерции 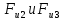прикладываем в центрах тяжести звеньев 2 и 3, и направляем вектора силы противоположно векторам ускорени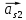й и .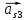

Вместо отброшенных звеньев 1 и 0 в шарнирах А и В прикладываем соответствующие реакци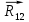и и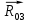 . Разложим неизвестную реакцию шарнира A на составляющие: 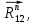действующую по линии АВ, и тангенциальную 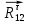, перпендикулярную этому направлению.

Уравнение равновесия полученной системы имеет вид:
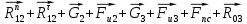=0. (3.4)




Уравнение равновесия (3.4) содержит четыре неизвестных: 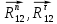, величина и точка приложения 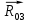. Для упрощения расчетов точку приложения 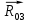считаем известной (точка В), тогда остается три неизвестных.

Найдем значение тангенциальной составляющей реакции 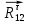из уравнения моментов всех сил, действующих на втором звене, относительно точки В.
Звено 2: 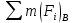=0, или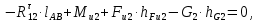

где плеч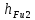и и 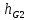измеряются на чертеже группы (в мм) и умножаются на масштабный коэффициент: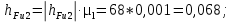



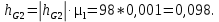
Тогда величина тангенциальной составляющей реакции в шарнире А


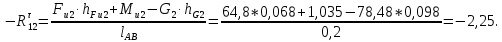
В результате проведенных вычислений в уравнении равновесия (3.4) осталось только две неизвестные.

Определение оставшихся неизвестных выполним с помощью плана сил. Масштабный коэффициент плана сил, H/мм, определим по формуле:


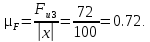
где 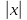– произвольный отрезок, изображающий на плане сил вектор силы инерции ползуна 3.

Переведем в масштабный коэффициент плана сил остальные силы, мм:










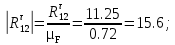
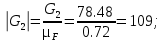
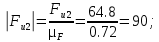
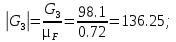
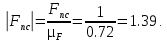
По полученным величинам строим план сил в выбранном масштабном коэффициенте.

Из плана сил определим значение нормальной составляющей реакции, H, равно


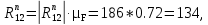
Значение реакций в шарнирах А и В, H, равно




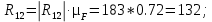
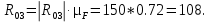
3.3. Силовой расчёт начального звена
Силовой расчёт механизма заканчивается силовым расчётом начального звена. В точке А на звено 1 со стороны отброшенного звена 2 действует реакция 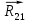, которая была определена ранее:
.
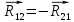Кроме этого, на звено 1 действуют реакция стойки 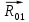, которая определяется из силового многоугольника звена 1, и уравновешивающий момент МУР, подлежащий определению.

Составим уравнение равновесия звена 1 в форме суммы моментов сил относительно точки О:


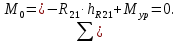
Откуда


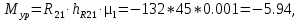
где h_R21 – плечо силы R₂₁ относительно точки О.

Для определения реакции 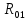составляем векторное равенство всех сил, действующих на начальный механизм: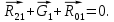


В соответствии с этим уравнением строим план сил начального звена.

Из силового многоугольника находим реакцию :


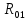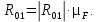
3.4. Проверка силового расчёта с помощью

метода рычага Н.Е. Жуковского
Рычагом Н.Е. Жуковского для данного механизма называется жесткая ферма, имеющая вид повернутого на 90^о (в любую сторону) плана скоростей механизма, закрепленного в полюсе.

Теорема Н.Е. Жуковского о рычаге заключается в следующем. Если силы, действующие на механизм, перенести, не меняя их направления, в соответствующие точки рычага Жуковского, то при равновесии механизма рычаг Жуковского также будет находится в равновесии.

Заменяем момент пары сил шатуна 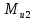парой сил 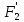и 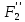, предварительно определив величину этих сил:
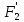и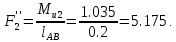

Для определения величины уравновешивающей силы составим сумму моментов всех сил, действующих на данную систему относительно полюса повернутого плана скоростей.



,
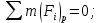
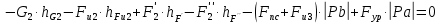где 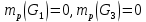, т.к. линия действия векторов проходят через полюс плана скоростей точку P.

Плечи 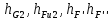, |Pb|,|Pa| находим из рычага Жуковского.

Следовательно, уравновешивающая сила, Н








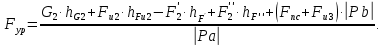
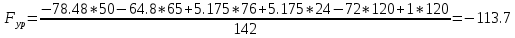
Уравновешивающий момент, H⋅м,

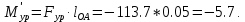
Проверка силового расчёта:
.
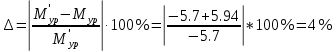где 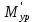– величина, найденная по методу Жуковского;

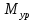– величина, найденная в ходе силового расчёта
Если величина, найденная по методу Жуковского, совпадает или отличается на 5-7% от величины найденной в ходе рассмотренного силового расчёта, считается, что силовой расчёт выполнен правильно.

4. ПРОЕКТИРОВАНИЕ ЭВОЛЬВЕНТНОГО

ЗАЦЕПЛЕНИЯ

См. лист 2 графической части проекта.
Необходимо выполнить следующее:

1. Выбрать величины коэффициентов смещения х₁ и х₂ для нарезания шестерни и колеса;

2. Произвести геометрический расчёт зубчатой передачи внешнего эвольвентного зацепления;

3. Построить картину зацепления, изобразив на каждом колесе по три зуба. Выделить линию зацепления, активную линию зацепления и активные профили зубьев.

4. Определить по данным картины зацепления коэффициент перекрытия зубчатой передачи и сравнить его с результатами аналитического расчёта. Оценить погрешность.


4.1 Расчет основных геометрических параметров зубчатой передачи
Исходные данные:

.

Число зубьев шестерни, колеса z1 = 11, z2 = 32;

Модуль m = 4;

Угол профиля α = 20°;

Коэффициент высоты головки 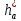= l

Коэффициент радиального зазора с* = 0,25
По таблице 4.1 выбираем коэффициенты смещения:

1. Сумма коэффициентов смещения:

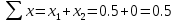
2. Угол зацепления :
,
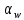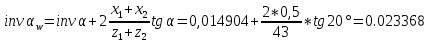Угол 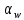находим по таблице эвольвентной функции, так полученное значение эвольвентной функции __________ соответствует углу = ___.

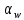3. Межосевое расстояние:





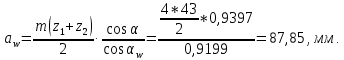
4. Радиусы делительных окружностей:



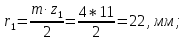
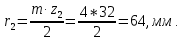
5. Делительное межосевое расстояние:

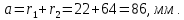
6. Коэффициент воспринимаемого смещения – отношение воспринимаемого смещения к модулю:

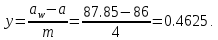
7. Коэффициент уравнительного смещения:

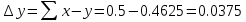
8. Радиусы начальных окружностей:



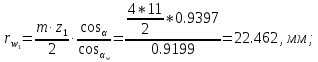
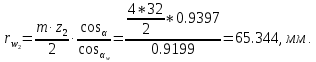
9. Проверка вычислений:
Сумма радиусов начальных окружностей должна быть равна межосевому расстоянию (с той же степенью точности):

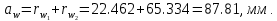
10 Радиус вершин зубьев:



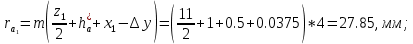
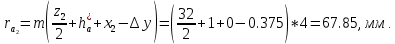
11. Радиусы впадин зубьев:




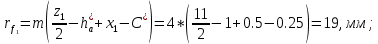
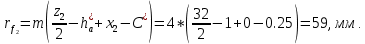
12. Проверка вычислений:
Высота зуба должна быть одинакова:

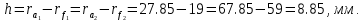
Если проверка не получилась, следует искать арифметическую ошибку в расчётах.
13. Толщина зубьев по дуге делительной окружности:
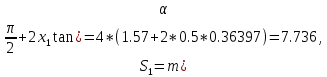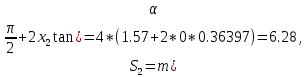мм;

мм.
14. Радиусы основных окружностей:
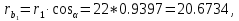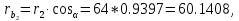мм;

мм.
15. Угловой шаг:




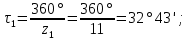
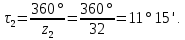
16. Углы профиля в точке на окружности вершин:







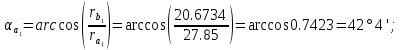
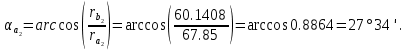
17. Толщина зубьев по окружности вершин:







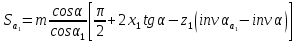
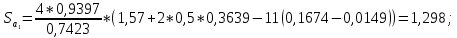
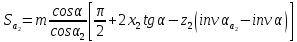
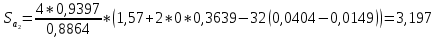
Проверка вычислений:
С увеличением радиуса толщина зуба колеса с внешним зацеплением уменьшается, поэтому в расчётах должно соблюдаться условие:
18. Коэффициент толщины зубьев по окружности вершин:



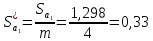
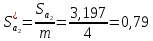
19. Коэффициент торцового перекрытия:

---

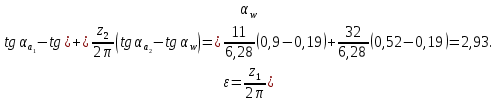
4.2. Построение картины эвольвентного зацепления

Выбирается масштаб построения, его следует выбрать таким, чтобы высота зуба составляла 40-50 мм.



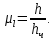
где 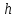– расчетная высота зуба, мм;

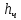– чертежная высота зуба, мм.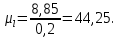

Определяем чертежные размеры колес передачи (таблица 4.2)
Таблица 4.2

Чертежные размеры колес 1 и 2, мм.

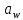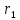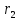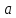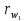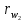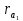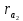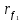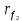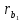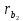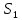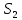87,85	22	64	86	22,46	65,34	27,85	67,85	19	59	20,67	60,14	7,75	6,28

---

По данным табл. 4.2 на листе 2 графической части проекта строим картину эвольвентного зацепления, изобразив по три зуба каждого из колес.
1. На листе откладывает в выбранном масштабе межосевое расстояние = .

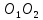2. Из центров 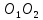проводим радиусы и начальных окружностей.

3. Откладываем и строим основные окружности радиусами

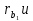
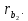
4. Через точку касания начальных окружностей – полюс зацепления Р проводим линию зацепления N-N, которая должна касаться основных окружностей в точках А и В. Для нахождения точек А и В от полюса Р откладываем отрезки:


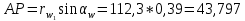
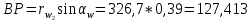
5. На следующем этапе производится построение эвольвентной части профиля зуба. Начальное положение производящей прямой, точка которой описывает эвольвенту зуба, совпадает с положением линии зацепления N-N.

6. Отрезок АР делим на четыре равные части, получаются точки 1, 2, 3, 4 (А3 = 32 = 21 = 1P). Если отложить такие отрезки за точкой А, получаются точки 5, 6, 7. Из точки А влево и вправо проводим дуги, равные длинам этих отрезков, до пересечения с основной окружностью. Получим точки Р', 1', 2', 3', 4', 5', 6' на основной окружности;

7. Точки Р', 1', 2', 3', 4', 5'… соединяем радиусами с центром вращения О2, а затем перпендикулярно этим радиусам проводим касательные к основной окружности.

8. На касательных откладываем отрезки 1'1''; 2'2''; 3'3'' …, соответственно равные отрезкам Р1; Р2; Р3…. Соединяя точки Р1; 1''; 2''; 3'' … плавной кривой, получаем эвольвенту, являющуюся частью профиля зуба.

9. Строим делительные окружности обоих колес

---

Смотрите также файлы

• Я, Писарева Татьяна Федоровна, в 1986 году окончила Калининское медицинское училище по специальности Сестринское дело.docx

• Курсового проекта.docx

• Обострение хронического периодонтита.docx

• Картель договоренность о единой сбытовой политике.docx

• 83саба Блім.docx