где

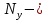число узлов.



Для решения этим методом произвольно направляем токи в ветвях. Заземляем любой узел, например узел “с”, и составляем для оставшихся трех узлов уравнения по первому закону Кирхгофа.

Составляем систему уравнений:







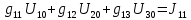
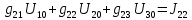
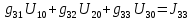
Далее необходимо рассчитать проводимости узлов. Собственная проводимость узла складывается из проводимостей ветвей, сходящихся в узле, и берётся со знаком плюс, проводимость же ветви, соединяющей узлы, берётся со знаком минус.

Для начала рассчитаем собственные проводимости узлов:







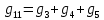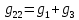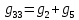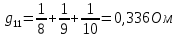
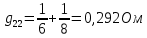
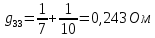
Теперь найдем проводимости ветвей, соединяющих узлы:







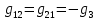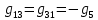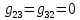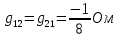
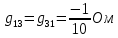
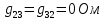
Следующим шагом находим значения задающих токов:







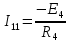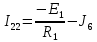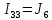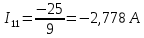
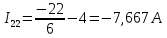
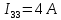
Подставляем найденные данные в систему уравнений: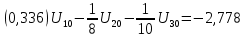







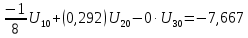
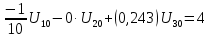
Решив систему уравнений, мы получим:







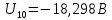
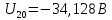
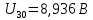
Зная напряжения узлов, можно без труда вычислить токи в ветвях.

Рассчитаем токи в ветвях:

4. 
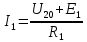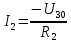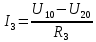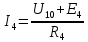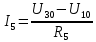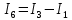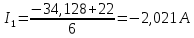
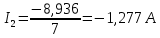
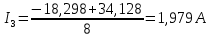
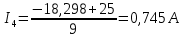
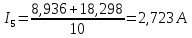
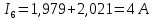
   Сравнение результатов расчета
   

Результаты расчетов обеими методами сводим в таблицу №3.

Таблица 3 – Результаты расчетов

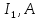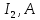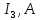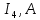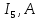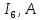М.К.Т		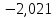		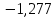		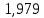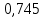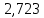4
М.У.П		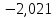		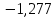		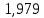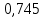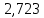4

5. 
   Расчет тока в ветви методом эквивалентного генератора
   

Применяя метод эквивалентного генератора, определяем ток в одной ветви. Выберем 1^ю ветвь.



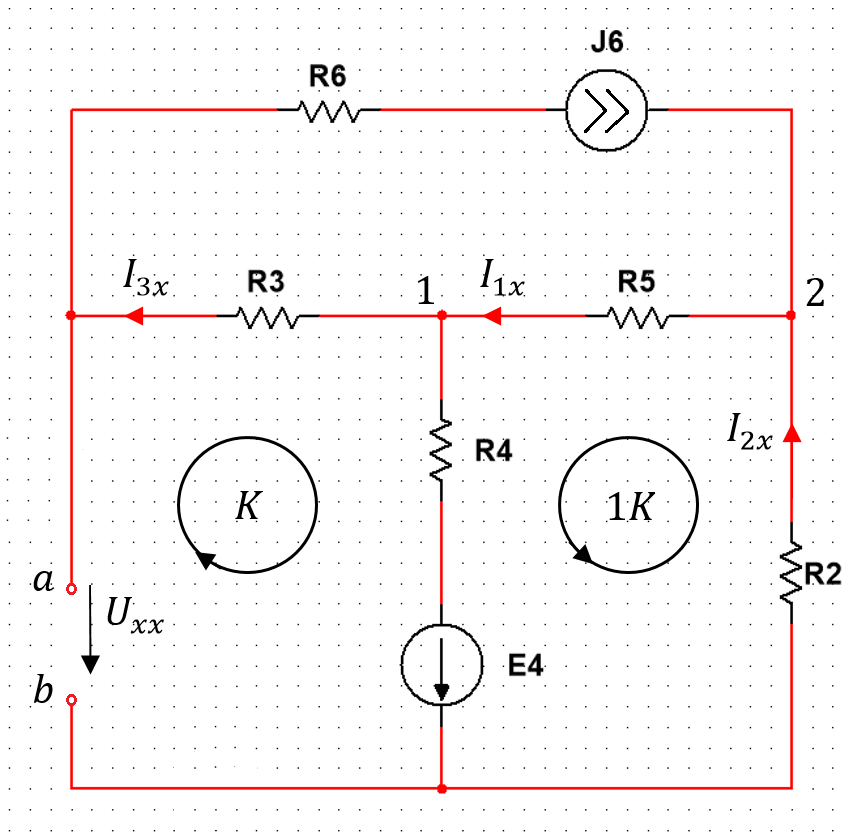
Рисунок 3 — Разомкнутая схема

Разорвем ветвь и рассчитаем режим холостого хода, то есть определим напряжение на свободных зажимах. Это напряжение и будет являться значением эквивалентной ЭДС.

Определим 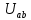по выражению:

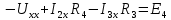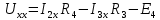Определим 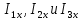c помощью законов Кирхгофа.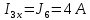



Составим систему уравнений: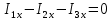





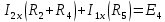
Решив систему уравнений, мы получаем следующие ответы:







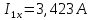
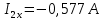
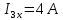
Определим



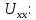
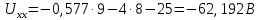
Сопротивление эквивалентного генератора равно сопротивлению между зажимами а и b, при условии, что все источники напряжения равны нулю (заменены внутренними сопротивлениями), а источники тока образуют разрыв цепи, как показано на рис. 4.



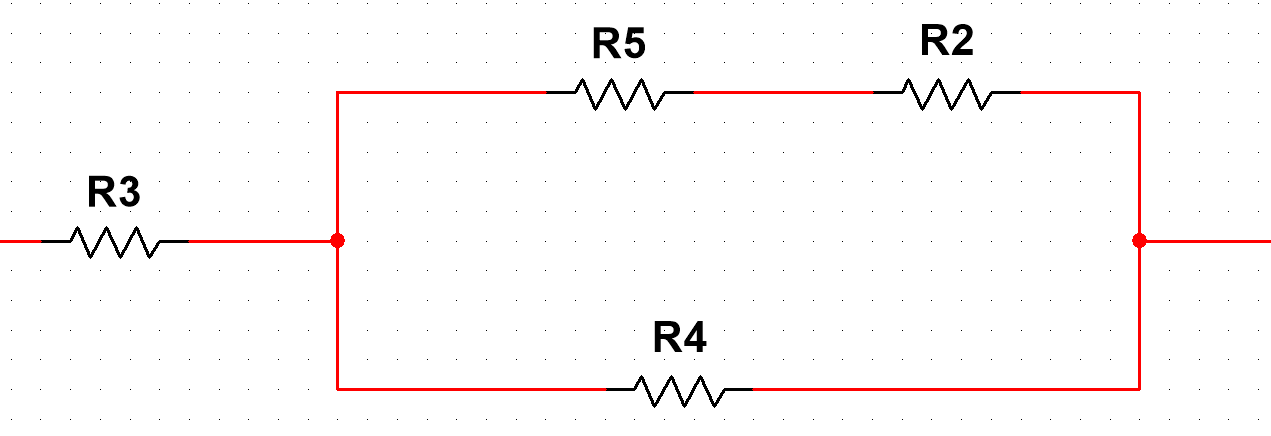
Рисунок 4 – Схема сопротивлений эквивалентного генератора

Определим полное сопротивление генератора:







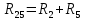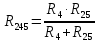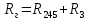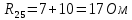
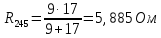
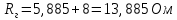
Для нахождения нужного нам тока упростим схему на рис. 5 и приведём её к следующему виду:



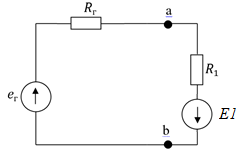
Рисунок 5 – Упрощенная схема

Исходя из схемы, можно воспользоваться следующей формулой для расчёта нужного нам тока:



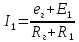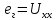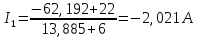
Значение этого тока совпадает с расчетами другими методами.

6. 
   Баланс мощностей
   

Проверяем правильность решения задачи составлением баланса мощностей.

Мощность, отдаваемая источниками энергии в цепь:





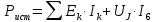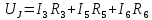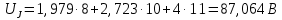
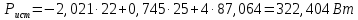
Мощность, потребляемая цепью, с учетом внутренних сопротивлений источников ЭДС:



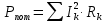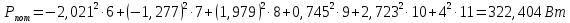
Баланс мощностей сходится, следовательно, токи определены, верно. Незначительным расхождением допускается пренебречь.

---

Смотрите также файлы

• Имажинизм как этап творчества С. Есенина.docx

• Сценарий Название Упрямая лошадь.docx

• Геометрия пні бойынша кнтізбеліктаырыпты жоспар. 20222023 оу жылы. за мерзімді жоспар.doc

• Задание Лицо привлечено к уголовной ответственности за незаконную предпринимательскую деятельность при сдаче в аренду жилого помещения третьим лицам без регистрации в качестве индивидуального предпринимателя.docx

• И в перемещениях для осесимметричной задачи теории упругости, общее решение.docx