Файл: II. Тестовые задания Кинематика поступательного и вращательного движения материальной точки 1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 1362
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
262. Коэффициент затухания – это физическая величина, …
1. показывающая во сколько раз уменьшается амплитуда колебаний за период
2. обратная времени, по истечении которого амплитуда колебаний уменьшается в «е» раз
3. обратная числу колебаний, по завершению которых амплитуда колебаний уменьшается в «е» раз
4. обратная числу колебаний, по завершению которых амплитуда колебаний уменьшается до нуля
5. обратная времени, по истечении которого амплитуда колебаний уменьшается до нуля
263. Шарик радиусом 10 см и массой 0,5 кг, подвешенный к нити длиной 20 см, совершает затухающие колебания в среде с коэффициентом затухания 2 кг·с-1. Коэффициент сопротивления среды равен … с-1.
1. 0,14 2. 1 3. 2 4. 4 5. 8
264. За 10 с амплитуда пружинного маятника массой m= 0,1 кг уменьшилась в е раз. Коэффициент затухания
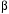 и коэффициент сопротивления среды
и коэффициент сопротивления среды  равны …
равны …1.
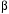 = 1;
= 1;  = 0,01 кг·с-1
= 0,01 кг·с-12.
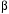 = 0,1;
= 0,1;  = 0,1 кг·с-1
= 0,1 кг·с-13.
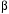 = 0,1;
= 0,1;  = 0,02 кг·с-1
= 0,02 кг·с-14.
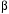 = 0,01;
= 0,01;  = 0,04 кг·с-1
= 0,04 кг·с-15.
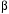 =
= 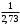 ;
;  = 0,02 кг·с-1
= 0,02 кг·с-1265. Период Т затухающих колебаний груза массой m на пружине жесткостью k можно рассчитать по формуле … (
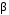 – коэффициент затухания,
– коэффициент затухания, 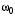 – циклическая частота свободных незатухающих колебаний колебательной системы).
– циклическая частота свободных незатухающих колебаний колебательной системы).1.
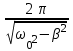 2.
2. 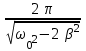 3.
3. 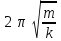 4.
4. 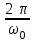 5.
5. 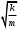
266. За время релаксации амплитуда затухающих колебаний …
1. увеличивается в 2 раза
2. уменьшается в 2 раза
3. увеличивается в e раз
4. уменьшается в e раз
5. не изменяется
267. Если период колебаний 2,5 с, коэффициент затухания 2 с-1, то логарифмический декремент затухания равен ….
1. 0,8 2. 1,25 3. 5 4.
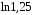 5.
5. 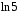
268. За один период амплитуда колебаний математического маятника с логарифмическим декрементом затухания
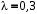 уменьшится в …раз.
уменьшится в …раз.1. 0,3 2. 0,37 3. 1,35 4. 2,73 5. 3,33
269. Логарифмический декремент затухания – это физическая величина, …
1. показывающая во сколько раз уменьшается амплитуда колебаний за период
2. обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается до нуля
3. обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается в «е» раз
4. обратная промежутку времени, за которое амплитуда колебаний уменьшается в «е» раз
5. обратная промежутку времени, за которое амплитуда колебаний уменьшается до нуля
270. Логарифмический декремент затухания колебаний маятника λ. Если амплитуда колебаний уменьшилась в n раз, то маятник совершил … колебаний.
1.
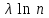 2.
2. 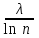 3.
3. 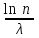 4.
4. 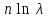 5.
5. 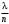
271. Период затухающих колебаний Т = 4 с. Добротность системы Q = 5. Логарифмический декремент затухания λ равен …
1. 20 2. 1,57 3. 1,25 4. 0,80 5. 0,63
272. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания λ = 1,6. Добротность системы (Q) равна …
1. 0,4 2. 0,79 3. 1,96 4. 2,5 5. 6,4
273. При сложении двух одинаково направленных колебаний, описываемых соответственно уравнениями
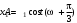 м и
м и 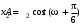 м получается колебание с амплитудой А, равной … м.
м получается колебание с амплитудой А, равной … м.1.
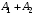
2.
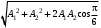 3.
3. 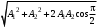
4.
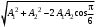 5.
5. 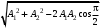
274.Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной …
1. 0 2.
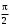 3.
3. 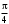 4.
4. 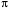 5.
5. 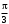
275. При сложении одинаково направленных гармонических колебаний одной частоты с амплитудами 10 см и 6 см, возникло колебание с амплитудой 14 см. Разность фаз складываемых колебаний равна … град.
1. 30 2. 45 3. 60 4. 90 5. 120
276. Складываются два колебания одинакового направления с амплитудами А1 = 3 см и А2 = 4 см. Чему равна разность фаз этих колебаний
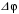 (в радианах), если амплитуда А результирующего колебания равна 5 см?
(в радианах), если амплитуда А результирующего колебания равна 5 см?1. 0 2.
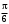 3.
3. 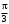 4.
4. 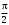 2.
2. 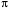
277. Складываются два колебания одинакового направления с амплитудами А1 = 3 см и А2 = 4 см. Амплитуда А результирующего колебания равна 6,1 см. Разность фаз складываемых колебаний равна … рад.
1. 0 2.
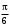 3.
3. 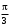 4.
4. 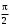 5.
5. 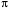
278. Складываются два колебания одинакового направления с амплитудами А1 = 3 см и А2 = 4 см и разностью фаз
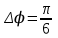
рад. Амплитуда А результирующего колебания равна … см.
1. 1,0 2. 6,08 3. 6,77 4. 5,0 5. 7
279. Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами
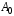 . При разности фаз
. При разности фаз 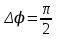 амплитуда результирующего колебания равна …
амплитуда результирующего колебания равна … 1.
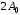 2.
2. 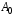
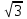 3. 0 4.
3. 0 4. 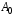
 5.
5. 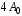
280. Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами
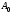 . При разности фаз
. При разности фаз 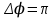 амплитуда результирующего колебания равна …
амплитуда результирующего колебания равна … 1.
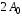 2.
2. 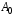
 3. 0 4.
3. 0 4. 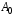
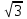 5.
5. 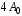
281. Длина волны, распространяющейся в воздухе, равна 1 м. Разность фаз
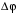 колебаний двух точек, лежащих на луче и отстоящих друг от друга на расстоянии 2 м, равна …
колебаний двух точек, лежащих на луче и отстоящих друг от друга на расстоянии 2 м, равна …1.
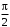 2.
2.  3.
3.  4.
4. 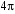 5. 0
5. 0282. Длина волны, распространяющейся в воздухе, равна 2 м. Разность фаз
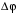 колебаний двух точек, лежащих на луче и отстоящих друг от друга на расстоянии 1 м, равна …
колебаний двух точек, лежащих на луче и отстоящих друг от друга на расстоянии 1 м, равна …1.
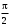 2.
2.  3.
3.  4.
4. 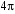 5. 0
5. 0283. При сложении двух происходящих в одном направлении колебаний, описываемых соответственно уравнениями
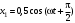 м и
м и 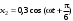 м, получается гармоническое колебание с амплитудой, равной … м.
м, получается гармоническое колебание с амплитудой, равной … м.1. 0,34 2. 0,44 3. 0,58 4. 0,7 5. 0,8
284.Колебания с частотой 40 Гц распространяются в воздухе со скоростью 400 м/с. Соседние точки пространства, колебания в которых происходят в противофазе, находятся на расстоянии … м.
1. 400 2. 40 3. 20 4. 10 5. 5
285. Если расстояние между точками бегущей волны, распространяющейся в стали равно 2,5 м, а колебания в них отличаются по фазе на
 , то частота звуковых колебаний равна … Гц. Скорость звука в стали равна 5 км/с.
, то частота звуковых колебаний равна … Гц. Скорость звука в стали равна 5 км/с. 1. 200 2. 500 3. 1000 4. 2500 3. 5000
286. В результате сложения двух гармонических колебаний одинакового направления с частотами
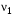 = 1000 Гц и
= 1000 Гц и 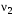 = 1002 Гц получаются колебания с периодически изменяющейся амплитудой (биения). Период биений равен …
= 1002 Гц получаются колебания с периодически изменяющейся амплитудой (биения). Период биений равен …1. 1 мс 2. 10 мс 3. 50 мс 4. 0,5 с 5. 1 с
287. При сложении двух гармонических колебаний одинакового направления с частотами
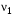 = 1000 Гц и
= 1000 Гц и 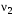 (
(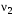 >
>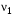 ) получают колебания с периодически изменяющейся амплитудой (биения). Период биений равен 20
) получают колебания с периодически изменяющейся амплитудой (биения). Период биений равен 20