Файл: Практическая работа 1 по дисциплине Теория вероятностей и математическая статистика вариант 5 студентка группы зукд121.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Владимирский государственный университет имени
Александра Григорьевича и Николая Григорьевича Столетовых»
(ВлГУ)
Практическая работа № 1
по дисциплине
«Теория вероятностей и математическая статистика»
вариант № 5
Выполнил:
студентка группы ЗУКд-121,
Корнилова В.В.
Проверил:
Мищенко З.В.
Владимир
2023
Элементы комбинаторики
Сколькими способами можно выбрать 6 пирожных в кондитерской, где есть 4 разных сорта пирожных?
Ответ: существует 84 различных способа выбора пирожных.
Элементы теории вероятностей
Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.
Неблагоприятные исходы:
5,15,25,35,45,50,51,52,53,54,55,56,57,58,59,65,75,85,95 – 19
P(A)=1−19100=0,81
Ответ: 0,81
Теоремы сложения и умножения вероятностей
В партии деталей 12 стандартных изделий и 3 нестандартных. 5 деталей, выбранных наудачу, проверяют на соответствие стандарту. Найти вероятность того, что среди них не окажется нестандартных.
р = m/n
n - число сочетаний из 15 по 5 равно 3003
m- число благоприятных результатов, число сочетаний из 12 по 5 равно 792
искомая вероятность 792 / 3003 = 0,2637.
Формула полной вероятности
Из 1000 экземпляров однотипного товара 300 принадлежат первой партии, 500 - второй и 200 - третьей. В первой партии 6%, во второй 5%, в третьей 4% бракованного товара. 1) Определить вероятность того, что наудачу выбранный экземпляр бракованный. 2) Наудачу выбранный экземпляр оказался стандартным, найти вероятность того, что он принадлежит третьей партии.
По формуле нахождения вероятности ,число благоприятных исходов делим на число всех исходов :
P = m/n
1) 300/100*6 = 18 – брак 1 партии
500/100*5 = 25 – брак 2 партии
200/100*4 = 8 – брак 3 партии
18+25+8 = 51 – всего брака
P = 51/1000 = 0.051
2) P = 200 / 1000 = 0.2
Формула Бернулли
Типография гарантирует вероятность брака переплета книг 0.0001. Книга издана тиражом 25000 экземпляров. Какова вероятность того, что в этом тираже только одна книга имеет брак переплета?
Для решения этой задачи можно использовать формулу Бернулли, которая применяется в случае, когда исходы бинарны (например, брак/не брак) и вероятность успеха (в данном случае, вероятность отсутствия брака) не изменяется при каждом испытании.
В данном случае вероятность успеха равна p = 1 - 0.0001 = 0.9999, так как типография гарантирует брак в 0.0001 случаев. Вероятность неудачи q = 1 - p = 0.0001.
Так как в тираже из 25000 экземпляров мы ищем вероятность только одного бракованного экземпляра, то воспользуемся формулой Бернулли для k = 1:
P(k = 1) = C(25000, 1) * p^1 * q^(25000 - 1)
где C(25000, 1) = 25000 - число сочетаний 25000 по 1.
Подставляем значения:
P(k = 1) = 25000 * 0.9999 * 0.0001^24999
P(k = 1) ≈ 0.0025
Таким образом, вероятность того, что только один экземпляр из 25000 имеет брак переплета, составляет примерно 0.0025, или около 0.25%.
Дискретные и непрерывные случайные величины
Автомобиль на пути встретит 4 светофора, каждый из которых пропустит его с вероятностью 0,6. Найдите математическое ожидание и дисперсию числа светофоров до первой остановки.
X - дискретная случайная величина.
Вероятность того, что машина попала на запрещающий сигнал 1-го светофора:
P(X=0)=(1-0,5)=0,5
Вероятность того, что машина попала на запрещающий сигнал 2-го светофора, проехав на 1-м светофоре:
P(X=1)=0,5(1-0,5)=0,5·0,5=0,25
Вероятность того, что машина попала на запрещающий сигнал 3-го светофора, проехав при этом на первых двух светофорах:
P(X=2)=0,5·0,5(1-0,5)=0,25 ·0,5=0,125
Вероятность того, что машина попала на запрещающий сигнал 3-го светофора, проехав при этом на первых трёх светофорах:
P(X=3)=0,5·0,5·0,5(1-0,5)=0,125 ·0,5=0,0625
Вероятность того, что машина проехала все четыре светофора:
P(X=4)=0,5 ·0,5 ·0,5 ·0,5=0,0625
Теперь можем показать вид закона распределения X:
x(i) 0 1 2 3 4
p(i) 0,5 0,25 0,125 0,0625 0,0625
Проверим:
Σp(i)=0,5+0,25+0,125+0,0625+0,0625=1
Дисперсия:
D(X)=Σ(x(i))²p(i) -(Σx(i)p(i))²=0²·0,5+1²·0,25+2²·0,125+3²·0,0625+4²·0,0625-(0·0,5+1·0,25+2·0,125+3·0,0625+4·0,0625)²=0,25+0,5+0,5625+1-(0,25+0,25+0,1875+0,25)²=2,3125-0,9375²≈1,434
Числовые характеристики непрерывной случайной величины
Случайная величина Х задана функцией распределения F(x). Найти: а) функцию плотности распределения f(x); б) математическое ожидание M(X); в) дисперсию D(X) и среднее квадратическое отклонение σ(X); г) построить графики функций F(x) и f(x).
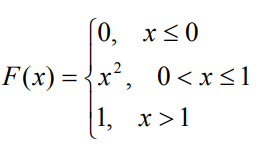
Найдем плотность распределения f(x), как производную от функции распределения F(x):
f(x)=(F(x))′=2·x
Плотность распределения f(x):
0, x ≤ 0
2·x, 0< x <1
0, x ≥ 1
Математическое ожидание.
M(x)= ∫abx·f(x)·dx
Найдем интеграл:
∫x·2·x·dx
Вычислим определенный интеграл:
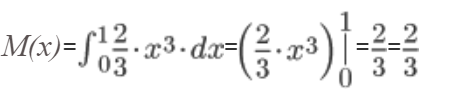
Дисперсия.
D(x)=∫abx2·f(x)·dx-M(x)2
Найдем интеграл:
∫x2·2·x·dx
∫nan·dx
Вычислим определенный интеграл:
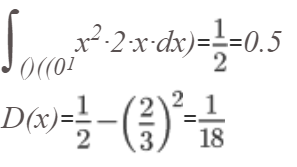
Среднеквадратическое отклонение.
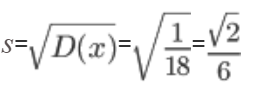
построить графики функций F(x) и f(x).
F(x)
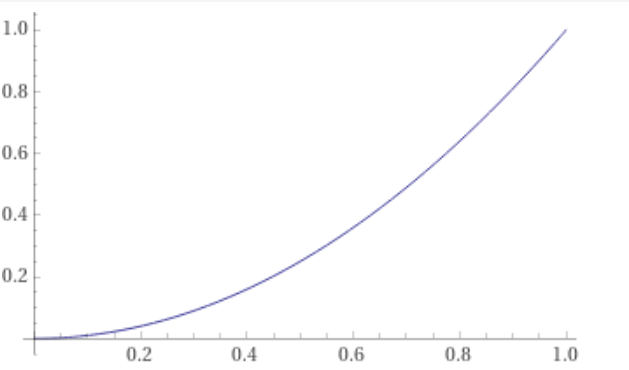
f(x)
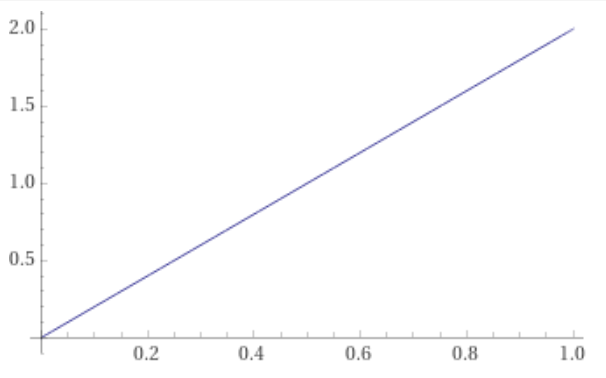
Нормальное распределение
15% продукции фирмы представляют изделия второго сорта. Магазин получил 1000 изделий. Какова вероятность того, что в полученной партии продукция второго сорта составит 15%±2%?
Для решения этой задачи мы можем использовать нормальное распределение, так как мы имеем достаточно большую выборку изделий (1000) и знаем вероятность получения изделия второго сорта (15%).
Сначала определим стандартное отклонение для выборки из 1000 изделий:
стандартное отклонение = sqrt(1000 * 0.15 * 0.85) = 8.08
Затем мы можем найти z-значение для нижней границы (13%):
z = (0.13 - 0.15) / 0.00808 = -2.48
И для верхней границы (17%):
z = (0.17 - 0.15) / 0.00808 = 2.48
P(-2.48 < Z < 2.48) = 0.9852 - 0.0148 = 0.9704
Таким образом, вероятность того, что в полученной партии продукция второго сорта составит 15%±2%, равна 0.9704, или примерно 97.04%.
Показательное распределение
98% топливных насосов дизельных тракторов выходит из строя после 3000 моточасов. Какова вероятность того, что насос выйдет из строя в интервале времени от 2000 до 2500 моточасов?
Для решения этой задачи мы можем использовать экспоненциальное распределение, так как мы имеем дело со временем до отказа (выхода из строя) топливного насоса.
Пусть λ будет интенсивностью отказов (выходов из строя) топливных насосов. Тогда мы знаем, что вероятность отказа после 3000 моточасов равна 0.98, что означает, что среднее время до отказа (среднее время работы) составляет:
1/λ = 3000 моточасов
λ = 1/3000 = 0.0003333 моточасов^(-1)
Теперь мы можем использовать функцию плотности вероятности экспоненциального распределения, чтобы найти вероятность отказа в интервале от 2000 до 2500 моточасов:
P(2000 < X < 2500) = ∫[2000, 2500] λ * e^(-λ*x) dx
Вычисляя этот интеграл, мы получаем:
P(2000 < X < 2500) = e^(-λ*2000) - e^(-λ*2500) = e^(-0.666) - e^(-0.833) ≈ 0.0593
Таким образом, вероятность того, что топливный насос выйдет из строя в интервале времени от 2000 до 2500 моточасов, составляет около 0.0593, или примерно 5.93%.