Файл: Контрольная работа по дисциплине Мат задачи энергетики студентка 2 курса группы Б. Элэ. Эс. 21. 61 Иванова Н. В.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 52
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Тверской государственный технический университет»
(ФГБОУВПО «ТвГТУ»)
Контрольная работа по
дисциплине «Мат. задачи энергетики»
Выполнила:
студентка 2 курса
группы
«Б.ЭЛЭ.ЭС.21.61»
Иванова Н.В.
Номер зачетной книжки
021183
Проверил: Крупнов А. В.
Тверь
2023
1.1. Известно, что максимум нагрузок энергосистемы наступает в период с 8:30 до 11:30. Какова вероятность того, что максимальная нагрузка будет наблюдаться в последние 30 минут указанного промежутка, если график нагрузок формируется случайным образом?
Решение: Промежуток времени от 8:30 ч до 11 ч 30 переведем в минуты. 3 часа=180 минут. Обозначим событие A – максимальная нагрузка энергосистемы будет наблюдаться в последний час промежутка с 8:30 до 11:30. представим в виде отрезка АВ длиной в 180 единиц, а промежуток времени от 11 ч 00 мин до 11 ч 30 мин - в виде отрезка СВ длиной в 30 единиц .
180
30
Вероятность того, что максимальная нагрузка будет наблюдаться в последние 30 минут указанного промежутка равна
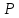 (A)
(A)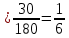 =0,16
=0,16 1.2 Территория подстанции представляет собой квадрат со стороной, равной d . В центре установлен стержневой молниеотвод, зона защиты которого ограничена окружностью с диаметром d (рис.1). Найдите вероятность попадания грозового разряда в незащищенную площадь подстанции.
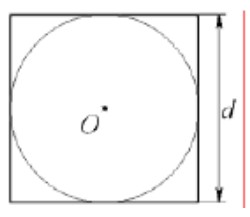
Пусть событие A – попадание грозового разряда в незащищенную площадь подстанции. Вероятность события A найдем как геометрическую вероятность по формуле:
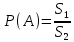
где
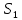 – незащищенная площадь подстанции,
– незащищенная площадь подстанции, 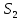 – площадь подстанции. Вычислим нужные площади. Площадь подстанции рассчитывается как площадь квадрата со стороной d :
– площадь подстанции. Вычислим нужные площади. Площадь подстанции рассчитывается как площадь квадрата со стороной d : 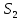 =
=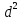
Чтобы вычислить незащищенную площадь подстанции, нужно из площади всей подстанции вычесть защищенную площадь, т.е. площадь окружности диаметром d:
 =
=  -
-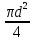
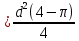
Тогда искомая впероятность P(A)
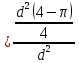 =
= 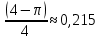
1.3 При увеличении напряжения может произойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов; вероятности отказа элементов соответственно равны 0,2; 0,3; 0,4. Определить вероятность того, что разрыва цепи не произойдет.
Решение. Пусть события А1, А2, А3 означают выход из строя соответственно первого, второго и третьего элементов. Их вероятности по условию соответственно равны: P (A1) = 0,2; P (A2) = 0,3; P (A3) = 0,4. Тогда вероятности противоположных событий A1, A2, A3 соответственно первый, второй и третий элемент не вышел из строя) равны:
P(
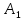 )= 1 -P(
)= 1 -P(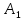 )=0,8; P(
)=0,8; P(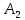 )= 0,7; P(
)= 0,7; P(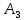 )=0,6
)=0,6Событие А, состоящее в том, что разрыва цепи не произошло, есть совмещение независимых событий
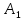 ,
, 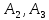 . Следовательно, по формуле получаем:
. Следовательно, по формуле получаем:P(
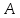 )= P(
)= P(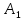 ) P(
) P(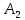 ) P(
) P(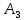 )=0,8
)=0,8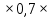 0,6= 0,336
0,6= 0,3361.4 Завод изготавливает электромагнитные реле с вероятностью дефекта p1 = 0,1. Изделия проверяются контролером, который обнаруживает дефект с вероятностью p2 = 0,8, но может по ошибке забраковать изделие, не имеющее дефект с вероятность p3 = 0,3. Найти вероятности следующих событий:
À1 – реле будет забраковано ошибочно;
А2 - изделие с дефектом будет отгружено покупателю;
А3 - реле будет забраковано по любой причине.
Решение. Рассмотрим следующие события: В1 – реле имеет дефект;
Â2 – контролер обнаружит имеющийся дефект; В3 – контролер забракует реле, не имеющее дефекта.
По условию задачи P (B1) = p1 = 0,1; P (B2) = p2 = 0,8; PB1 (B3 ) = p3 = 0,3. Событие А1 по смыслу означает: «изделие не имеет дефекта и изделие будет забраковано контролером», т .е. A1 = B1 × B3.
Тогда P (A1 ) = P (B1 × B3 ) = P (B1 )× PB1 (B3 ) = (1- p1 )× p3 = 0,9×0,3 = 0,27.
Событие А2 по смыслу означает: «изделие имеет дефект и контролер не обнаружит дефект», т.е. A2 = B1 × B2 .
Тогда P (A2 ) = P (B1 )×P (B2 ) = p1 ×(1- p2 ) = 0,1×0,2 = 0,02, т.к. события B и B2 независимые.
Событие А3 по смыслу означает: «изделие имеет дефект и контролер обнаруживает дефект или изделие не имеет дефекта и контролер забракует изделие», т.е. A3 = B1 × B2 + B1 × B3
P(A3 ) = P (B1 × B2 + B1 × B3 ) = P (B1 )×P (B2 ) + P(B1 )×PB1 (B3 ) =
=P1 ×P2 + (1- p1 )× p3 = 0,1×0,8 + 0,9×0,3 = 0,35.
1.5. По линии связи передаются два сигнала A и В соответственно с вероятностями 0,72 и 0,28. Из-за помех 1 6 часть A-сигналов искажается и принимается, как В -сигналы, а 1 7 часть переданных В -сигналов принимается, как A-сигналы. Определите: 1) вероятность того, что на приемном пункте будет принят A-сигнал; 2) если известно, что принят A-сигнал, какова вероятность того, что он же и был передан?
Пусть событие А - на приемном пункте появился А-сигнал. Введем гипотезы: НА - передан сигнал А, НВ - передан сигнал В. По условию P (Ha) = 0,72; P (Hb) = 0,28.
Вероятность того, что принят А-сигнал при условии, что он же послан, равна:
P(A/
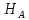 )= 1-
)= 1-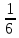 =
=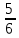
Вероятность того, что принят А-сигнал при условии, что послан В-сигнал, равна:
P(A/
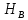 )= 1-
)= 1-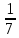
Отсюда по формуле полной вероятности получаем
P(А)= Р(
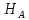 )
)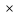 P(A/
P(A/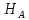 )+Р(
)+Р(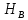
)
 P(A/
P(A/ )=0,27
)=0,27
 +0,28
+0,28 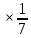 = 0,64
= 0,64б) вероятность приема А-сигнала при условии, что он же был передан, найдем по формуле Байеса:
P(
 /A)=
/A)=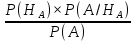 =
=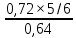 =
=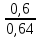
1.6 Потребитель может заключить договор о поставке электроэнергии в одну из трех энергосбытовых компаний. Вероятности обращения в каждую зависят от их тарифной политики и равны соответственно 1 p , 2 p и 3 p . Вероятность того, что к моменту обращения потребителя лимиты мощности у поставщика будут исчерпаны, составляет для первой компании 4 p , для второй – 5 p , для третьей – 6 p . Какова вероятность, что договор на поставку электроэнергии будет заключен.
Решение. Рассмотрим следующие случайные события:
А- потребитель заключит договор о поставке электроэнергии
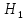 - потребитель направится в 1 компанию
- потребитель направится в 1 компанию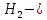 потребитель направится в 2 компанию
потребитель направится в 2 компанию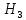 – потребитель направится в 3 компанию
– потребитель направится в 3 компаниюЯсно, что события -1, -2, -3 образуют полную группу событий и несовместны (мы считаем, что пассажир может направиться только в одну кассу). События -1, -2, —з являются гипотезами. Событие А может
 По формуле полной вероятности:
По формуле полной вероятности:P(А)= Р(
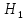 )
)
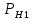 (A) +Р(
(A) +Р(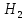 )
)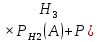 )
)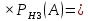
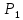 (1-
(1-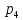 )+
)+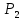 (1-
(1-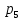 )+
)+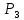 (1-
(1-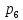 )
)1.7 Имеются три пары измерительных приборов по 30 штук в каждой. Число стандартных приборов в первой, второй и третьей партиях соответственно равно 20, 15, 10. Из случайно выбранной партии наудачу извлечены два прибора, оказавшимися стандартными. Найти вероятность того, что приборы были извлечены из третьей партии.
Решение. Обозначим через А событие — в каждом из двух испытаний была извлечена стандартный прибор.
Можно сделать три предположения (гипотезы): -1 — приборы извлекались из первой партии; -2 — приборы извлекались из второй партии; -3 —приборы извлекались из третьей партии.
Так как приборы извлекались из наудачу взятой партии, то вероятности гипотез одинаковы:
Р(
 )= Р(
)= Р( )= Р(
)= Р( )=
)= 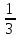
Найдем условную вероятность PH1 (A), т. е. вероятность того, что из первой партии будут последовательно извлечены два стандартных прибора:
 (А)=
(А)=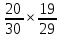 =
=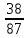
Найдем условную вероятность PH2 (А), т. е. вероятность того, что из второй партии будут последовательно извлечены (без возвращения) два стандартных прибора:
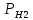 (А)=
(А)=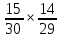 =
=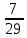
Найдем условную вероятность
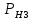 (А). Т. е. вероятность того,
(А). Т. е. вероятность того,что из третьей партии будут последовательно извлечены две стандартные детали: