Файл: Контрольная работа по дисциплине Мат задачи энергетики студентка 2 курса группы Б. Элэ. Эс. 21. 61 Иванова Н. В.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 61
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(А)=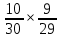 =
=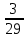
Искомая вероятность того, что обе извлеченные стандартные детали взяты из третьей партии, по формуле Бейеса равна:
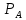 (
( )
)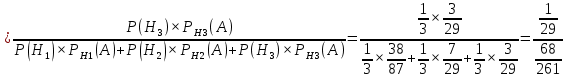 =
= 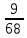
1.8 Среди реле, выпускаемых заводом, бывает в среднем 2% дефектных. Найти вероятность того, что среди взятых на испытание 25 реле двое из них будут неисправных. Каково наивероятнейшее число дефектных реле в рассматриваемой выборке из 25 деталей и какова его вероятность?
Решение. Здесь опыт заключается в проверке каждого из 25 реле на качество. Событие А - появление нестандартной детали; его вероятность Р = 0,02, тогда q = 0,98. Отсюда по формуле Бернулли находим:
P25 (2) =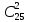
 (0,2)^2× (0,98)^23
(0,2)^2× (0,98)^23 0,025.
0,025.
Наивероятнейшее число нестандартных деталей в данной выборке вычисляется по формуле:
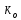 = [25 ¦ 0,02 + 0,02] = [1,24] = 1, а его вероятность равна
= [25 ¦ 0,02 + 0,02] = [1,24] = 1, а его вероятность равна
P25(1) = C1c × 0,02× (0,98)^24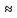 0,012
0,012
1.9 Вероятность поражения линии электропередачи при грозовом разряде составляет 0,8. Найдите вероятность того, что после четырех разрядов произойдет: а) хотя бы одно поражение ЛЭП; б) не менее трех поражений; в) не более одного поражения.
Решение. Здесь n = 4, p = 0,8, q = 0,2. а) Найдем вероятность противоположного события - в серии из четырех разрядов нет ни одного поражения ЛЭП:
Отсюда находим вероятность хотя бы одного поражения:
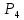 (к≥1)=1-0,0016=0,9984
(к≥1)=1-0,0016=0,9984
б) Событие В, заключающееся в том, что в серии из четырех разрядов произошло не менее трех поражений, означает, что было либо три поражения (событие С), либо четыре (событие D), т. е. В = С + D. Отсюда P (B) = P (C) + P (D); следовательно,
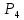
(к≥3)= (3)
(3)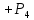 (4)=
(4)= 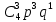 +
+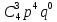 =4×
=4×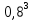 ×0.2+
×0.2+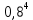 = 0,8192
= 0,8192
в) Аналогично вычисляется вероятность поражения не более одного раза:
 (к≥1)=
(к≥1)= (0)
(0)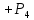 (1)= 0,0016+
(1)= 0,0016+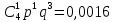 +4×
+4×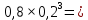 0,2576
0,2576
Задача 2.9. Результаты замеров мощности потребителя представлены в виде выборки:

Построить гистограмму и определить закон распределения, рассчитать выборочные: мат.ожидание, дисперсию и среднее квадратическое отклонение и оценить доверительные интервалы генерального мат.ожидания и среднеквадратического отклонения.
Решение:
п = 100
Для построения гистограммы вычислим относительные частот с шагом интервала h = 1,4 – это расстояние между точками).

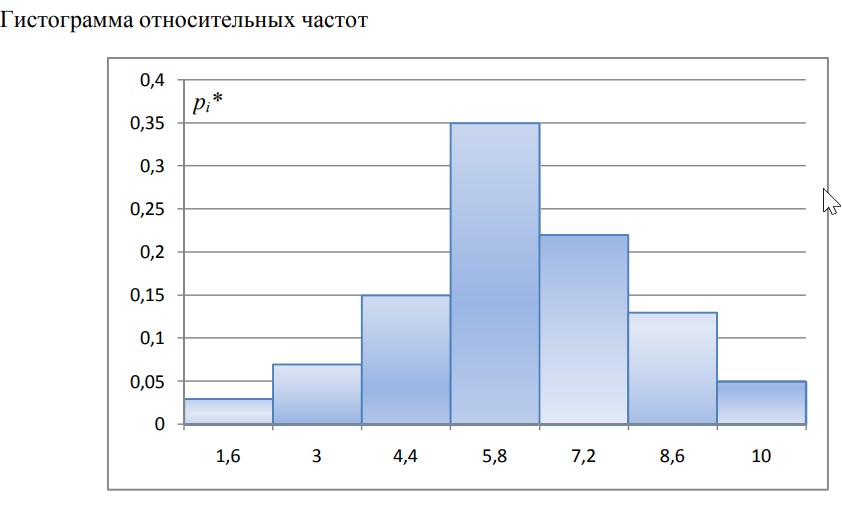
Выборочные: мат.ожидание, дисперсию и среднее квадратическое отклонение
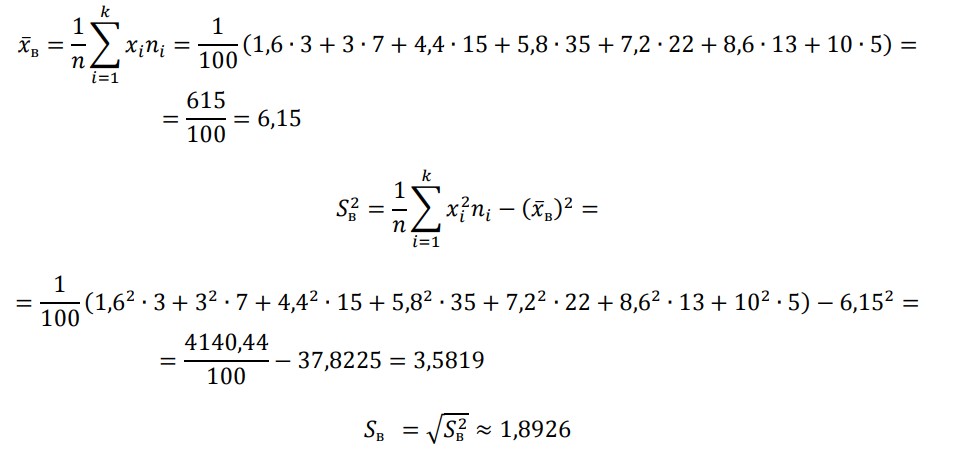
Доверительные интервалы генерального мат.ожидания и среднеквадратического отклонения
Математическое ожидание
Дисперсия неизвестна, объем выборки п = 100, доверительная вероятность = 0,95
Исправленная дисперсия
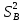 =
=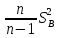 =
= 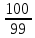 ×3,5819=3,6181
×3,5819=3,6181
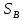 =
=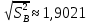
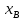 -
-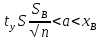 +
+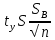
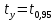 (n-1)=1,9842
(n-1)=1,9842
6,15-1,9842 6,15+1,9842
6,15+1,9842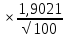
5,7726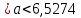
Среднеквадратическое отклонение
s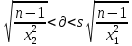
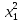 =
=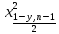 =
=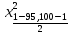 =
=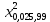 =77,046
=77,046
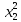 =
=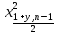 =
=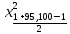 =
=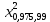 =123,23
=123,23
s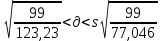
1,7049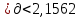
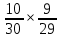 =
=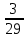
Искомая вероятность того, что обе извлеченные стандартные детали взяты из третьей партии, по формуле Бейеса равна:
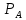 (
( )
)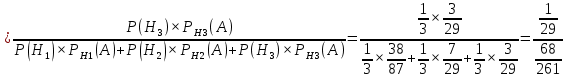 =
= 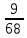
1.8 Среди реле, выпускаемых заводом, бывает в среднем 2% дефектных. Найти вероятность того, что среди взятых на испытание 25 реле двое из них будут неисправных. Каково наивероятнейшее число дефектных реле в рассматриваемой выборке из 25 деталей и какова его вероятность?
Решение. Здесь опыт заключается в проверке каждого из 25 реле на качество. Событие А - появление нестандартной детали; его вероятность Р = 0,02, тогда q = 0,98. Отсюда по формуле Бернулли находим:
P25 (2) =
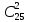
 (0,2)^2× (0,98)^23
(0,2)^2× (0,98)^23 0,025.
0,025.Наивероятнейшее число нестандартных деталей в данной выборке вычисляется по формуле:
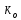 = [25 ¦ 0,02 + 0,02] = [1,24] = 1, а его вероятность равна
= [25 ¦ 0,02 + 0,02] = [1,24] = 1, а его вероятность равнаP25(1) = C1c × 0,02× (0,98)^24
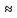 0,012
0,0121.9 Вероятность поражения линии электропередачи при грозовом разряде составляет 0,8. Найдите вероятность того, что после четырех разрядов произойдет: а) хотя бы одно поражение ЛЭП; б) не менее трех поражений; в) не более одного поражения.
Решение. Здесь n = 4, p = 0,8, q = 0,2. а) Найдем вероятность противоположного события - в серии из четырех разрядов нет ни одного поражения ЛЭП:
Отсюда находим вероятность хотя бы одного поражения:
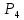 (к≥1)=1-0,0016=0,9984
(к≥1)=1-0,0016=0,9984б) Событие В, заключающееся в том, что в серии из четырех разрядов произошло не менее трех поражений, означает, что было либо три поражения (событие С), либо четыре (событие D), т. е. В = С + D. Отсюда P (B) = P (C) + P (D); следовательно,
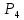
(к≥3)=
 (3)
(3)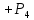 (4)=
(4)= 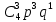 +
+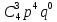 =4×
=4×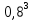 ×0.2+
×0.2+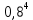 = 0,8192
= 0,8192в) Аналогично вычисляется вероятность поражения не более одного раза:
 (к≥1)=
(к≥1)= (0)
(0)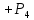 (1)= 0,0016+
(1)= 0,0016+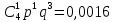 +4×
+4×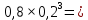 0,2576
0,2576Задача 2.9. Результаты замеров мощности потребителя представлены в виде выборки:

Построить гистограмму и определить закон распределения, рассчитать выборочные: мат.ожидание, дисперсию и среднее квадратическое отклонение и оценить доверительные интервалы генерального мат.ожидания и среднеквадратического отклонения.
Решение:
п = 100
Для построения гистограммы вычислим относительные частот с шагом интервала h = 1,4 – это расстояние между точками).


Выборочные: мат.ожидание, дисперсию и среднее квадратическое отклонение
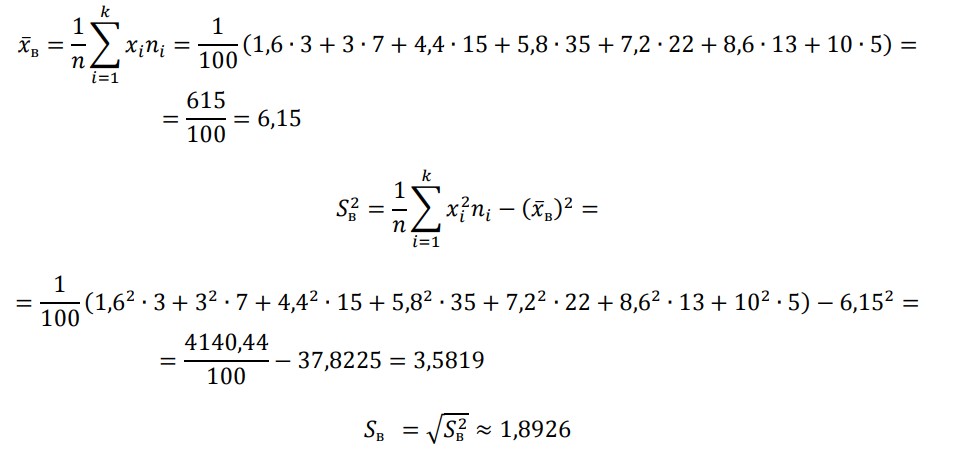
Доверительные интервалы генерального мат.ожидания и среднеквадратического отклонения
Математическое ожидание
Дисперсия неизвестна, объем выборки п = 100, доверительная вероятность = 0,95
Исправленная дисперсия
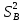 =
=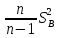 =
= 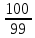 ×3,5819=3,6181
×3,5819=3,6181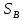 =
=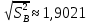
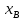 -
-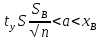 +
+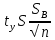
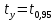 (n-1)=1,9842
(n-1)=1,98426,15-1,9842
 6,15+1,9842
6,15+1,9842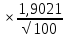
5,7726
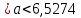
Среднеквадратическое отклонение
s
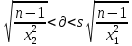
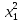 =
=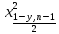 =
=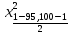 =
=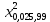 =77,046
=77,046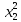 =
=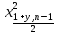 =
=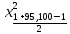 =
=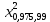 =123,23
=123,23s
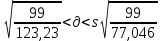
1,7049