Кардиоида

Кардио́ида — плоская кривая, описываемая произвольной точкой М окружности радиуса r, катящейся без проскальзывания извне по другой, неподвижной, окружности того же радиуса (рис. 1). Название кардиоиды происходит от греческих слов χαρδια – сердце, и ειδος – вид, вместе – сердцевидная.



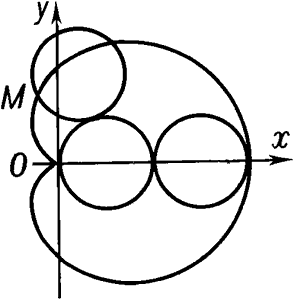
Рис. 1
Кардиоида впервые встречается в трудах французского учёного Луи Карре. Название кривой дал в 1741 году Джованни Сальвемини ди Кастиллоне.

«Спрямление», то есть вычисление длины кривой, выполнил Ла Ир, который открыл кривую независимо, в 1708 году. Также независимо описал кардиоиду голландский математик Й. Коерсма. В дальнейшем к кривой проявляли интерес многие видные математики XVIII—XIX веков.
Как и любую кривую, кардиоиду можно задать несколькими видами уравнений.

Пусть r �aa — радиусы окружностей, начало координат находится в крайней правой точке горизонтального диаметра неподвижной окружности (рис. 1). Тогда уравнения кардиоиды можно записать в следующих формах:

1. 
   В декартовых координатах:
   

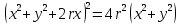
Как видно из уравнения, она является алгебраической кривой четвертого порядка и симметрична относительно оси абсцисс.

2. 
   Исходя из определения кардиоиды, она представляет собой эпициклоиду с модулем m, равным 1. Это обстоятельство позволяет сразу же записать параметрические уравнения кардиоиды, заменяя в параметрических уравнениях эпициклоид модуль m единицей. Будем иметь:
   

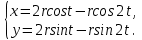(1)

3. 
   Чтобы получить полярное уравнение кардиоиды, удобно принять за полюс точку А (рис. 2), а полярную ось направить по оси абсцисс.
   

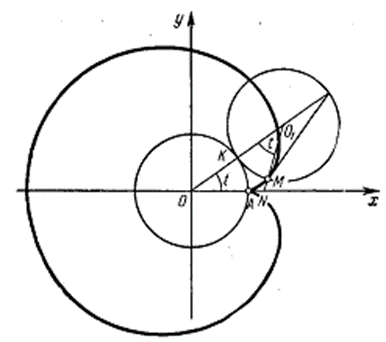
Рис. 2
Так как четырехугольник AOO₁M будет равнобедренной трапецией, то полярный угол j точки М окажется равным углу поворота производящего круга, т.е. параметру t. Учитывая это обстоятельство, заменим во втором уравнении системы (1) у через

---

rsint. Сокращая полученное таким образом равенство на sint, получим полярное уравнение кардиоиды:

ρ = 2r(1 - cosφ)

По виду этого уравнения можно заключить, что кардиоида является одной из улиток Паскаля. Она может быть определена, следовательно, как конхоида круга.



Рассмотрим некоторые свойства кардиоиды:

1. 
   Кардиоида является частным случаем улитки Паскаля при r=l
   
2. 
   Площадь фигуры, ограниченной кардиоидой, равна 6πr²
   
3. 
   Длина полной кардиоиды равна шестнадцати радиусам производящей окружности:
   

L_кард = 16r.

4. 
   Длина дуги от точки А до произвольной точки М:
   

s = 16rsin²( )

5. 
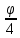   Касательная в произвольной точке кардиоиды проходит через точку окружности производящего круга, диаметрально противоположной точке касания кругов, а нормаль — через точку их касания.
   

Рассмотрим несколько методов построения кардиоиды.

1) Метод карандашных отрезков

Для построения кардиоиды с помощью карандашных отрезков начертим окружность и отметим на ней четное количество точек (N). Чем больше точек отмечено на окружности, тем более явно будет видна кардиоида.

Затем соединим точки в таком порядке 1-2, 2-4, 3-6, 4-8, 5-10, 6-12 и т.д. Контуры этих отрезков и дадут нам кардиоиду (рис. 3).



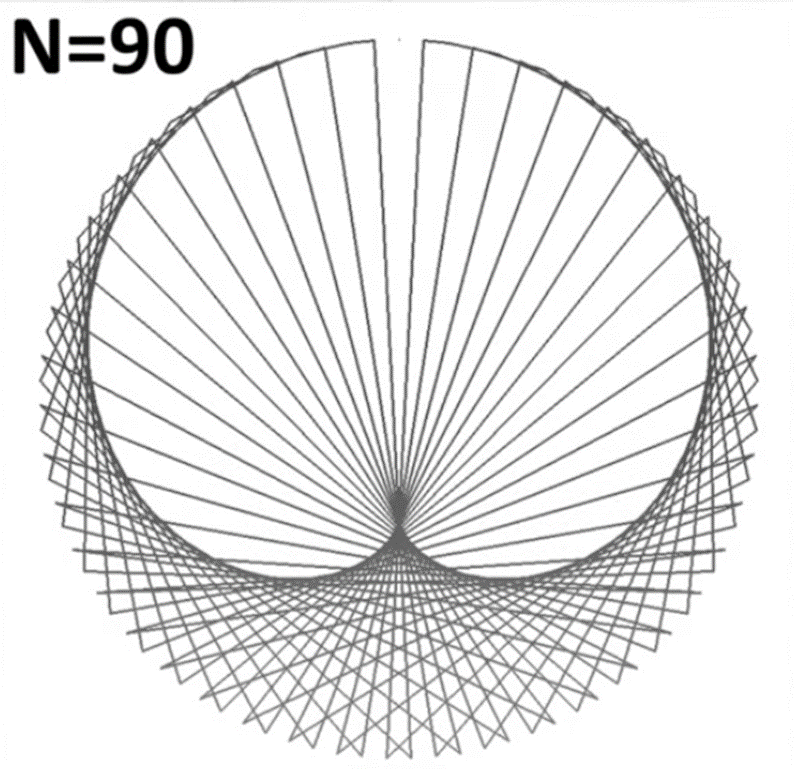
Рис. 3
2) С помощью диаметра заданной окружности

Начертим окружность радиусом a и центром в точке О, и выберем на ней произвольную точку М₀. Через точку М₀ проведем пучок лучей, пересекающих нашу окружность.

От точек В пересечения лучей с окружностью отложим вдоль каждого луча в обе стороны отрезки, равные диаметру нашей окружности и соединим концы этих отрезков (рис. 4).



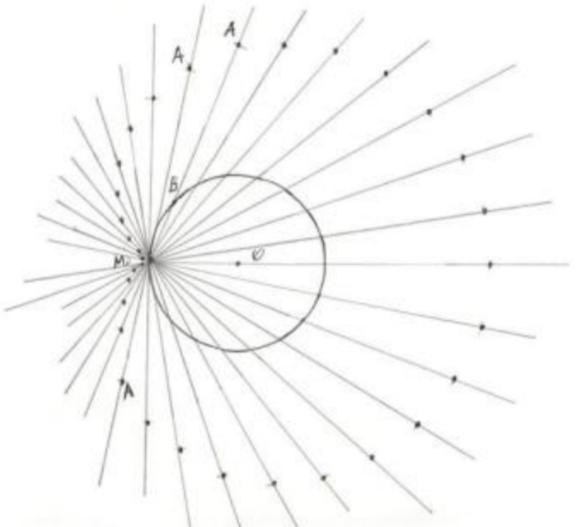
Рис. 4
3) В полярных координатах

Построить кардиоиду, заданную уравнением в полярных координатах

---

ρ = 4(1 – sin φ).

Составим таблицу, в которой приведены значения полярного угла φ_i (i = 1,16) и соответствующие им значения полярного радиуса ρ_i:

φi	ρi	φi	ρi	φi	ρi	φi	ρi
0	4		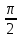0	π	4		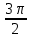8
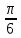	2		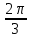≈0,6		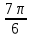6		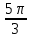≈7,4
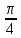	≈1,2		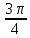≈1,2		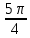≈6,8		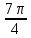≈6,8
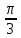	≈0,6		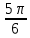2		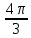≈7,4		6

Построив найденные точки M_i ( ρ_i; φ_i) в полярной системе координат и соединив их плавной линией, получим достаточно точное представление о кардиоиде (рис. 5).



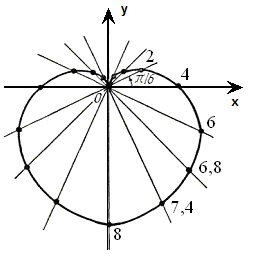
Рис. 5
Мы можем видеть кардиоиду в различных объектах живой и неживой природы (рис. 6).

---

Рис. 6

Неоценимо значение кардиоиды и в создании электронной музыки. Микрофон с кардиоидной диаграммой направленности безразличен к звуку, идущему сзади, обеспечивает максимальную нечувствительность к боковым звукам, обеспечивает максимальную акустическую изоляцию, защищает от неблагоприятных эффектов помещения, посторонних шумов, препятствует утечке сигнала (рис. 7).



Рис. 7

---

Смотрите также файлы

• Вопросы к семинару 1 по дисциплине менеджмент.docx

• 933 Работу защитил с Специальность.docx

• Задание 36. Наплавка дуговая, электрошлаковая, токами высокой частоты. Дуговая наплавка.docx

• Программа воспитания разработана в соответствии с Федеральным Законом Об образовании в Российской Федерации.doc

• Отчет о прохождении практики 5 дневник учебной практики 8 характеристика 10.docx