Файл: Семинару 1 по дисциплине Высшая математика 38. 03. 02. Менеджмент Управление бизнесом Очнозаочная форма обучения.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 38

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задание №1 к семинару №1 по дисциплине Высшая математика

38.03.02. Менеджмент – Управление бизнесом

Очно-заочная форма обучения
Выполнил студент 1 курса группы з-М22/УБ-У05

Агапцев Илья Владимирович
Задача 1. Вычислить пределы данных функций.
а)



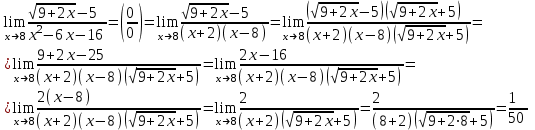
б) ;

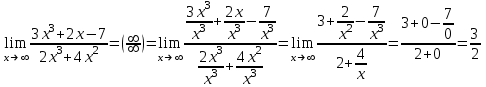в)

;

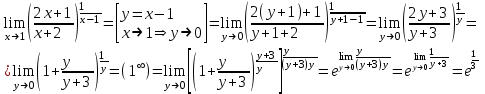г)



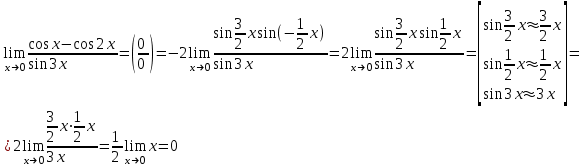
Задача 2. Определить то значение параметра А, для которого функция 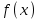будет непрерывной (если возможно). Сделать чертеж.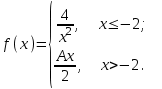


Данная функция определена и непрерывна на интервалах (-∞;-2],(-2;+∞).

Исследуем поведение функции в точке х=-2. Найдём односторонние пределы.


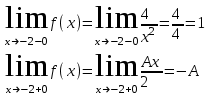
Функция будет непрерывна, если односторонние пределы будут равны, т.е. если 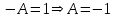, тогда функция будет иметь вид: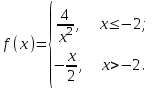


Сделаем чертеж:



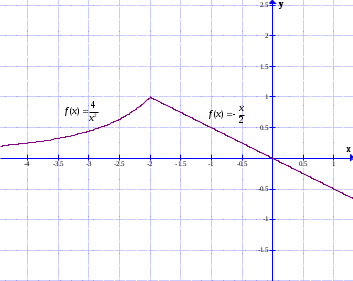
Ответ: При А=-1 функция непрерывна.

Задача 3. Исследовать функцию методами дифференциального исчисления и построить график.


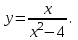
  1. Найдем область определения D(y). Очевидно D(y) = (–;-2), (-2,2), (2;+).

  2. Исследуем функцию на непрерывность при х=-2 х=2.



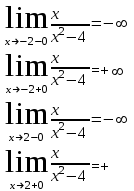
Значит, х=-2 х=2 – вертикальные асимптоты.

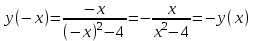  1. . Функция является нечетной.

  2. Определим критические точки. Для этого найдем производную y'.

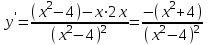. Тогда y' = 0 или 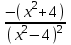=0 не имеет решения. Определим знак первой производной на интервалах.

y'(x)




– – –




-2 2

Значит, на промежутках (–;-2),(-2;2), (2;+) функция убывает. Значит, точек максимума и минимума нет.

  1. Определим точки перегиба. Для этого найдем вторую производную y'' функции:

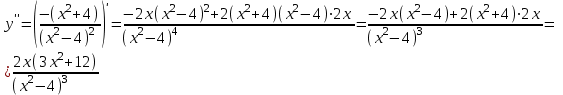; тогда y'' = 0 или 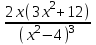=0– имеет решение при х=0. Получим, что при х=0 перегиб.

Определим знак второй производной на области определения.
y''(x)

– + – +

- 2 0 2

Таким образом, при x  (-;-2),(0; 2) график функции выпуклый, при x  (-2;0)0 (2;+ ) график функции вогнутый.

  1. Выясним, имеет ли функция асимптоты y=kx+b.



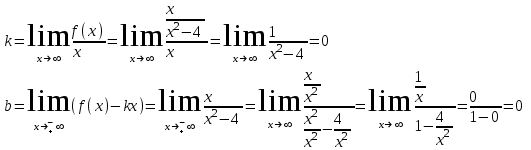
Асимптота у=0 является горизонтальной асимптотой.

7) По результатам исследования строим график функции:



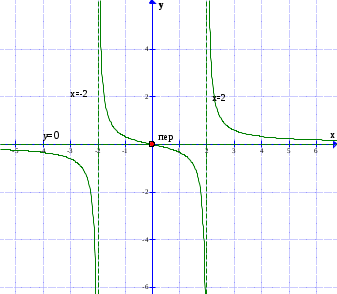
Задача 4. Найти все частные производные второго порядка, включая смешанную производную и дифференциал первого порядка от функции:

f = 8x2y – xcosy.


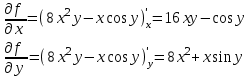
Тогда дифференциал первого порядка:






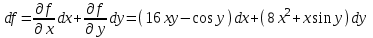
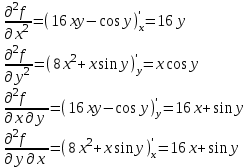
Задача 5. Исследовать на экстремум функцию f= x2 + 4xy – y2+2x+ 4y + 7.
Найдём стационарные точки.



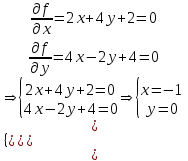
Получили точку С (-1,0) . Рассмотрим достаточное условие экстремума, для этого найдём производные второго порядка.



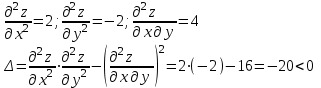
Т.к. ∆<0 , то в точке C(-1;0) нет экстремума0>

Смотрите также файлы