ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В целях изучения стажа рабочих завода проведена 36 %-ная механическая выборка, в результате которой получено следующее распределение рабочих по стажу работы:
| Стаж, число лет | Число рабочих, человек |
| До 5 | 12 |
| 5-10 | 18 |
| 10-15 | 24 |
| 15-20 | 32 |
| 20-25 | 6 |
| Свыше 25 | 8 |
| Итого: | 100 |
Вычислить:
1) средний стаж рабочих завода;
2)моду и медиану стажа рабочих;
3)средний квадрат отклонений (дисперсию), среднее квадратическое отклонение и коэффициент вариации;
4)с вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих всего завода.
Ответ:
-
Для вычисления среднего стажа просуммируем произведение середин интервалов и соответствующих частот и полученную сумму разделим на сумму частот.
| Стаж, число лет | Середины интервалов  |  |  |  |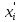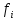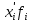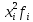
| До 5 | 2,5 | 12 | 30 | 75 |
| 5-10 | 7,5 | 18 | 135 | 1012,5 |
| 10-15 | 12,5 | 24 | 300 | 3750 |
| 15-20 | 17,5 | 32 | 560 | 9800 |
| 20-25 | 22,5 | 6 | 135 | 3037,5 |
| 25 и выше | 27,5 | 8 | 220 | 6050 |
| Итого | | 100 | 1380 | 23725 |
Найдем средний стаж по формуле
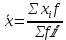
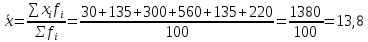
Средний стаж=13,8 лет
-
Вычислим моду и медиану стажа
Мода-варианта, которой соответствует наибольшая чистота
Мода вычисляется по формуле
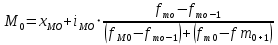
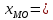15 начало модального интервала
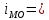5 величина интервала
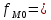32 частота модального интервала
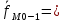24 частота интервала, предшествующего модальному
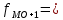6 частота интервала, следующего за модальным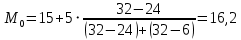
Медиана-варианта, находящаяся в середине ряда распределения
Расчет медианы производится по формуле
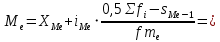
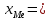10 - начало (нижняя граница) медиального интервала
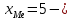величина интервала
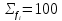- сумма всех частот ряда
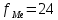- частота медиального интервала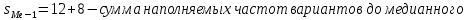
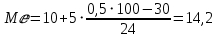
Таким образом, половина рабочих имеет стаж до 14,2 лет, другая половина более 14, 2 лет.
-
Дисперсия
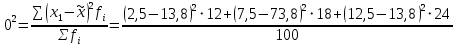
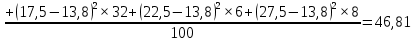
показывает среднее арифметическое квадратное отклонение
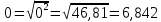
коэффициент
-
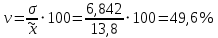
Предельная ошибка выборочной средней
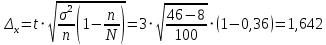
Где
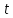– аргумент функции Лапласа. Границы в которых ожидается средний стаж от 12,158 до 15,442
13,8-1,642=12,158
13,8+1,642 = 15, 442