СОДЕРЖАНИЕ


ВВЕДЕНИЕ.

Исследование гетеропереходов представляет собой важный раздел физики полупроводниковых приборов, который сформировался в последние четыре десятилетия на основе изучения эпитаксиального выращивания полупроводников.

Барьеры на диаграмме энергетических зон, связанные с различием в ширине запрещенной зоны двух полупроводников открывают новые возможности для конструкторов.

Гетеропереходы используются в лазерах, вычислительной технике, интегральных схемах. Электрооптические свойства гетеропереходов нашли практическое применение в фототранзисторах и в солнечных элементах.

Однако в этой области имеется еще много нерешенных проблем, многие классы гетеропереходов еще ожидают своего тщательного изучения и применения.

Основная часть достижений в исследованиях гетеропереходов связана с использованием гетеропары GaAs-AlGaAs, в которой осуществлен так называемый идеальный гетеропереход. При этом использованы полупроводники с однотипной кристаллической решеткой, которые имеют настолько близкие значения постоянных своих решеток, что на границе не возникает электрически активных дефектов.

Однако физика и техника гетеропереходов имеют и другой важный аспект - создание, исследование и практическое применение неидеальных гетеропереходов. Такие структуры образованы поликристаллическими полупроводниками с несовпадающими констан­тами кристаллических решеток, зачастую и различных решеточных симметрии. В неидеальных гетеропереходах наблюдается большой набор различных эффектов и явлений, связанных с различными свойствами полупроводников по обе стороны границы, а также с появлением большого количества электрически активных дефектов на гетерогранице, принимающих участие в токопереносе, поглощении и излучении световых квантов.

Перспективность практического применения неидеальных гетеропереходов связана в первую очередь с более экономичной технологией создания поликристаллических гетероструктур в сравнении с монокристаллическими.

Одним из направлений в изучении неидеальных гетеропереходов является возможность применения критериев, разработанных в классической фотографической сенситометрии, к преобразователям оптического изображения в электрический сигнал на основе гетероперехода CdS-Cu₂S.

Целью данной работы является создание математической модели характеристической кривой и расчет основных сенситометрических характеристик (γ-коэфициент контрастности и S-фоточувствительность) формирователя сигнала изображения (ФСИ) на основе гетероперехода CdS-Cu₂S, используя в качестве исходных данных характеристики локальных центров в гетеропереходе.


ГЛАВА I. ГЕТЕРОПЕРЕХОД CdS-Cu₂S, ЕГО СВОЙСТВА И ТЕХНОЛОГИЯ ИЗГОТОВЛЕНИЯ.
§ 1. Общие свойства гетеропереходов.
Гетеропереходом называется контакт двух различных по химическому составу полупроводников. Если полупроводники имеют одинаковый тип проводимости, то они образуют изотипный гетеропереход. Если тип их проводимости различен, то получается анизотипный гетеропереход.

Для получения идеальных монокристаллических гетеропереходов без дефектов решетки и поверхностных состояний на границе раздела необходимо, чтобы у полупроводников совпадали типы кристаллических решеток, их периоды и коэффициент термического расширения. Для их получения периоды решеток должны совпадать с точностью

0,1%. Пример идеального гетероперехода: GaAS -AIGaAS [1].

---

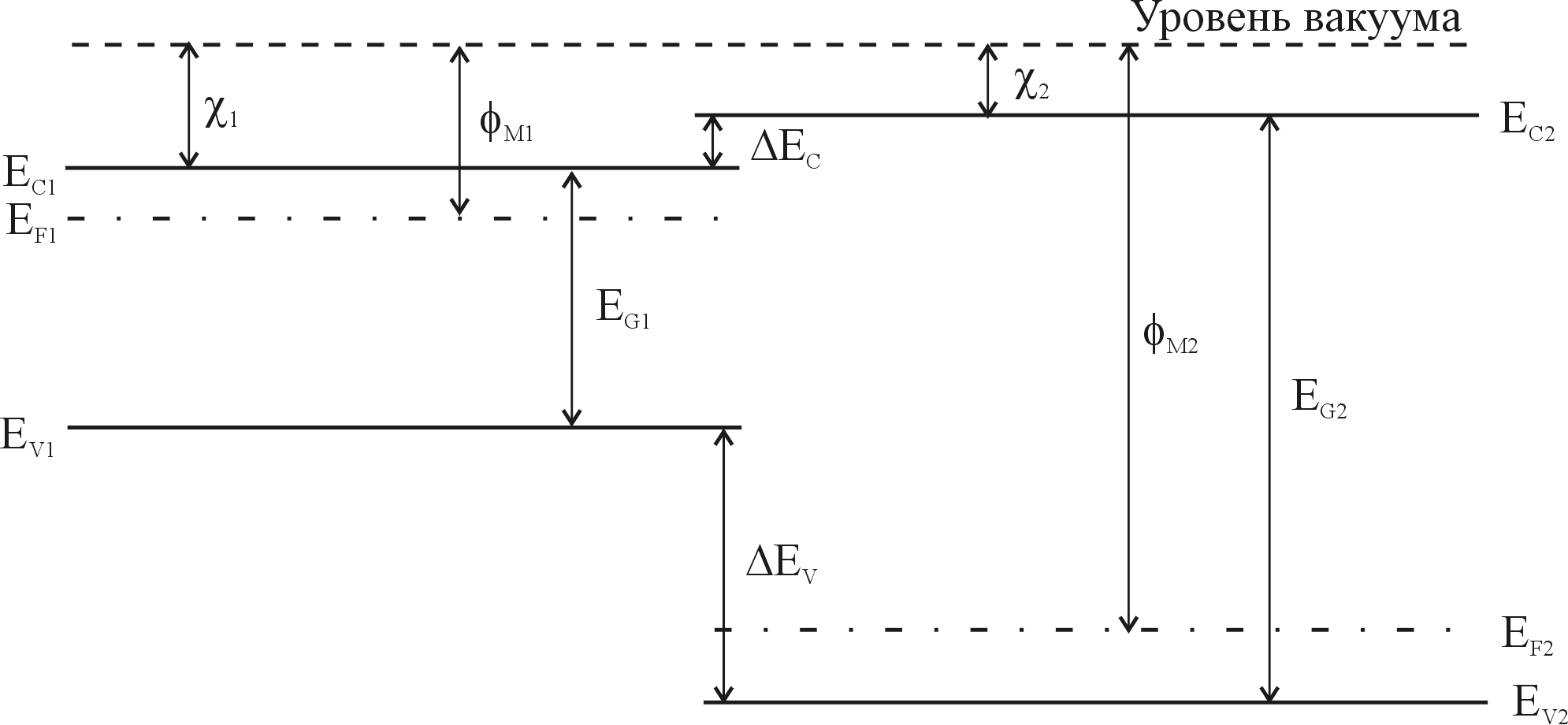
Модель зоны структуры идеального резкого гетероперехода без ловушек на границе раздела была предложена Андерсеном, который использовал результаты работы Шокли [2].На рис.1 приведена зонная диаграмма двух изолированных полупроводников, у которых различные значения ширины запрещенной зоны Еg , диэлектрической проницаемости , работы выхода _m и электронного сродства .Работа выхода и электронное сродство определяются как энергия, необходимая для удаления электрона с уровня Ферми Е_f и со дна зоны проводимости Е_c в вакуум соответственно. Различие в положении дна зоны проводимости полупроводников обозначено Е_c; а различие в положении потолка валентной зоны ΔE_v. На рисунке 1 показан случай, когда ΔЕ_c=(χ₁-χ₂).

Рис. 1. Зонная диаграмма двух изолированных полупроводников при условии электронейтральности

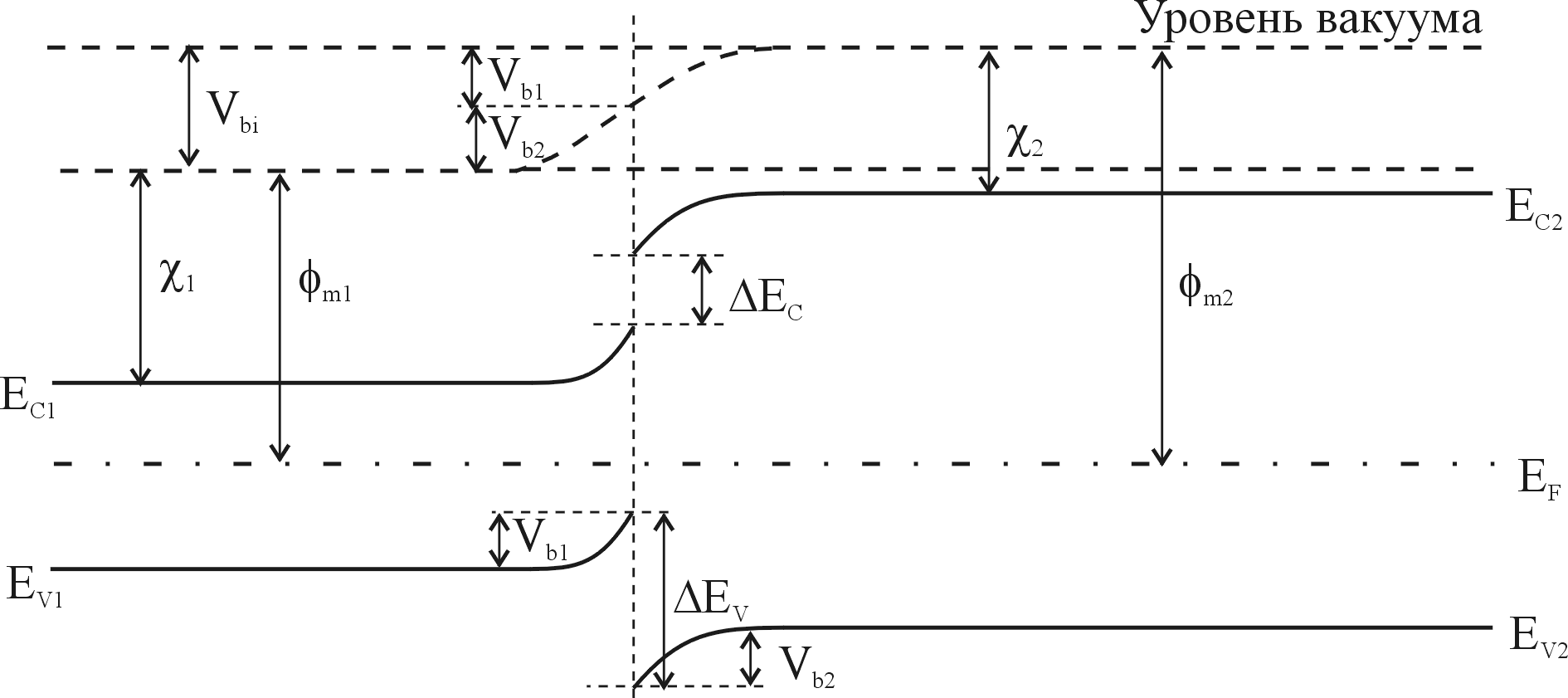
Зонная диаграмма анизотипного p-n - гетероперехода в равновесии, образованного этими полупроводниками приведена на рис.2.

Рис.2. Зонная диаграмма идеального анизотипного p-n гетероперехода при тепловом равновесии.

Положение уровня Ферми в равновесном состоянии должно быть одинаково по обе стороны перехода, а уровень энергии, соответствующий вакууму, должен быть параллелен краям зон и непрерывен. Поэтому разрыв в положении краев зоны проводимости и краев валентной зоны не связан с уровнем легирования.Полный контактный потенциал Vb_i. равен сумме потенциалов Vb₁+Vb₂, где Vb₁ и Vb2 - электростатические потенциалы равновесия состояния первого и второго полупроводников соответственно.Ширину обедненного слоя (W) в каждом полупроводнике и барьерную емкость (С) можно найти решив уравнение Пуассона для резкого перехода с каждой стороны границы раздела. Одним из граничных условий является непрерывность электрической индукции на границе раздела, т.е.

---

ε₁E₁= ε₂E₂. В результате имеем:

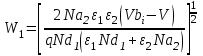	(1)
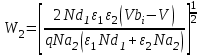	(2)
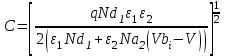	(3)

где Nd₁ - концентрация доноров в 1-м полупроводнике;Na₂ - концентрация акцепторов во 2-м полупроводнике.Отношение напряжений в каждом полупроводнике составляет:

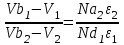(4)

где V=V₁+V₂ - полное приложенное напряжение.Вольт - амперная характеристика принимает вид:

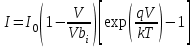(5)

где I - плотность тока.

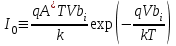(6)

---

Приведенное выражение отличается от вольт - амперной характеристики контакта металл-полупроводник множителем I₀, а также характером зависимости от температуры. Обратный ток не имеет насыщения, а при больших V линейно возрастает с напряжением. В прямом направлении зависимость I от допускает аппроксимацию экспоненциальной функцией, т.е. 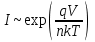.Механизмы протекания тока.В резком гетеропереходе благодаря разрывам ΔE_c и ΔE_v высоты потенциальных барьеров для электронов и дырок разные. Поэтому при прямом смещении в гетеропереходе обычно происходит односторонняя инжекция носителей из широкозонного полупроводника в узкозонный.Инжектированные носители (в данном случае дырки) должны преодолеть потенциальные барьеры (“пики”), возникающие из-за разрывов зон. Механизмы протекания тока через эти барьеры, дополнительные по сравнению с p-n - переходом (туннельный и термоинжекционный) зависят от величины смещения на гетеропереходе, температуры, а также от степени легирования полупроводников.В плавном гетеропереходе заряда на неосновные носители заряда действует внутреннее электрическое поле ε_i, возникающее вследствие изменения E_g. При прямом смещении в этом случае также происходит односторонняя инжекция дырок в более узкозонную часть.Фотоэффект.Как и в p-n переходе фотоэффект в гетеропереходе возникает за счет пространственного разделения в поле объемного заряда носителей, возбужденных светом. При освещении полупроводника со стороны широкозонного полупроводника в узкозонном поглощаются фотоны с энергией:

Eg12

(7)

где h - постоянная Планкаυ - частота излучения.Широкозонный полупроводник служит в этом случае "окном", прозрачным для света, поглощаемого в узкозонном слое, и защищает область генерации неравновесных электронно-дырочных пар от рекомбинационных потерь на поверхности кристалла [2].§ 2. Модели токопереноса в гетеропереходе CdS – Cu₂S.Система CdS-Сu₂S представляет собой неидеальный анизотипный гетеропереход у которого различие постоянных кристаллических решеток контактирующих полупроводников CdS (5.832 Å) и Cu

---

₂S (5.601 Å) составляет 4%. Столь значительное различие периодов решеток при формировании гетероперехода создает высокую плотность дислокаций несоответствия на поверхности раздела. Оборванные связи в дислокациях приводят к появлению энергетических уровней в запрещенной зоне, ответственных за захват носителей или за их рекомбинацию и оказывают существенное влияние на перенос заряда через обедненную область [3,4].Было предложено немало моделей, объясняющих процессы, протекающие в гетеропереходе. Вид зонной диаграммы и характер токопрохождения не могут быть описаны в рамках модели Андерсона, учитывающей только ток, текущий благодаря инжекции.Для гетероперехода известно несколько вероятных механизмов протекания тока через область барьера, реализующихся в зависимости от внешних условий: электронный и дырочный токи при фотовозбуждении (1,2), термоэмиссионный (3), эмиссионно-рекомбинационный (4), туннельно-рекомбинационный ток (5,6) (См. рис.3) .

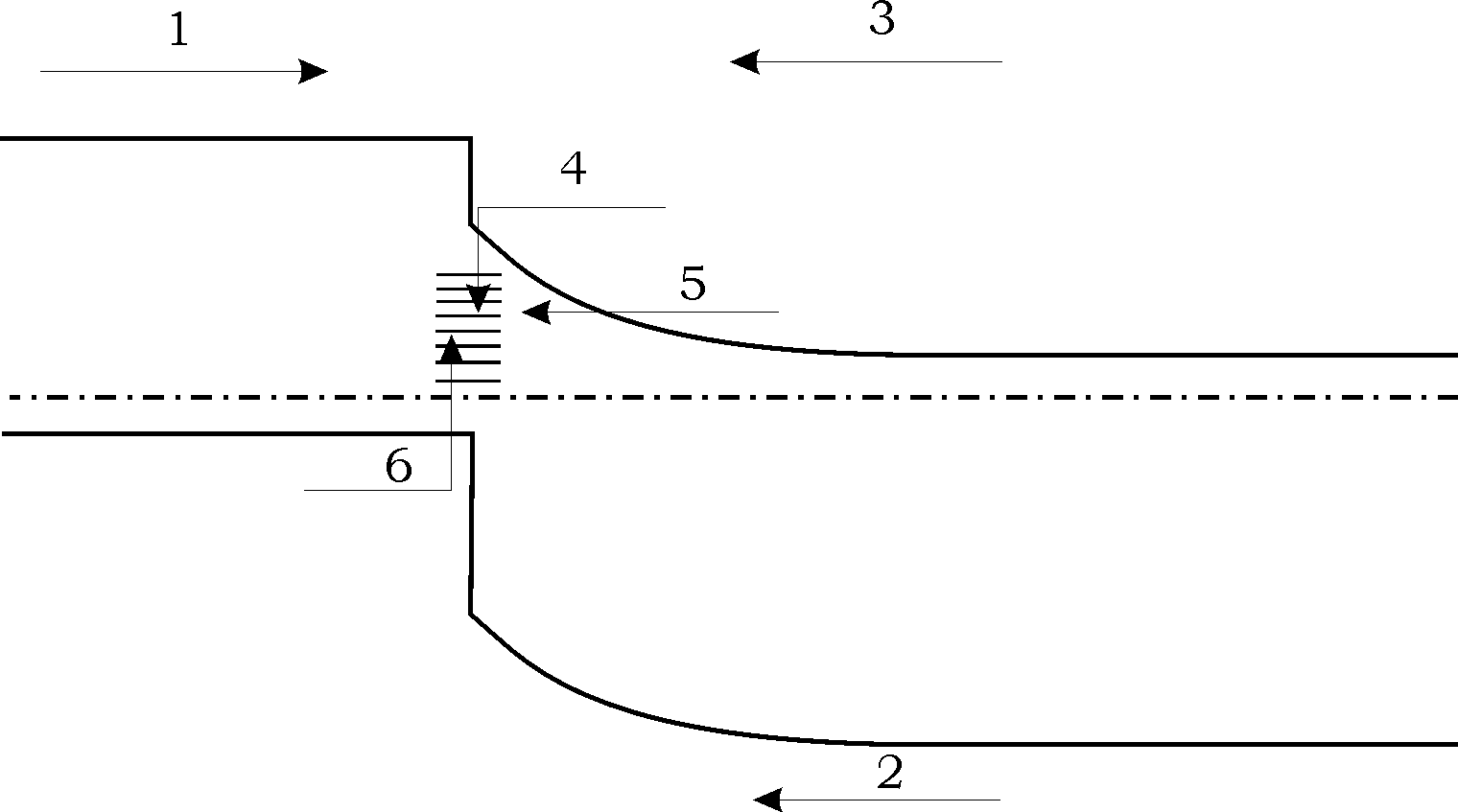Рис.3. Вероятные механизмы токопереноса в области пространственного заряда гетероперехода CdS-Cu2S.

Для согласования теории с данными экспериментов, Бьюб предложил модель туннелирования электронов через "зубец" в зоне проводимости. Ширина "зубца", а следовательно и вклад туннельного тока в вольтамперную характеристику определялась глубокими уровнями дефектов в ОПЗ. Однако этот случай реализуется далеко не всегда.Модель многоступенчатого туннелирования через эти состояния с последующей рекомбинацией на гетерограницах предложили Райбен и Фойхт для Ge-GaAs и Мартинуцци для CdS-Cu₂S. При таком подходе, однако, невозможно точно определить вероятность туннельных переходов с одного уровня на другой и не учитывается ограничение туннельной проводимости скоростью рекомбинационных процессов на границе раздела.В ряде публикаций [5,6,7,8] был предложен туннельно-прыжковый механизм токопереноса. Здесь учтены статистические распределения носителей и их взаимодействие с фононами. Определена также вероятность "прыжка" между соседними локальными состояниями.

---

Смотрите также файлы

• Решите задачу. При ответе используйте ссылки на действующие статьи фз О государственной регистрации юридических лиц и ип.docx

• Группа Прочитайте эпизод с начала повести до слов И всётаки моя ночь была лучше дня! Вот как это было. Найдите в нём пейзажи. Докажите, что описание петербургского ночного пейзажа отличается лаконичностью и неразрывной связью с человеком..docx

• Лабораторная работа по дисциплине Правоведение Группа Вл22Э191в Студент С. А. Арбузова Преподаватель.docx

• І. теориялы Блім.docx

• Книга для заботливых ищущих родителей, психологов, педагогов, дефектологов и методистов СанктПетербург 1998.doc