ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 121
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
теңсіздігі Коши теңсіздігіне қарсы болғандықтан, дұрыс емес, олай болса,  .
.
Теңсіздіктерді осы сияқты дәлелдеу үшін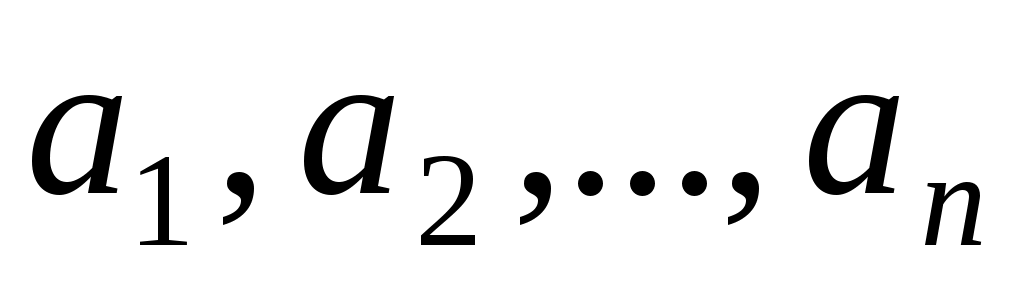 ,
, 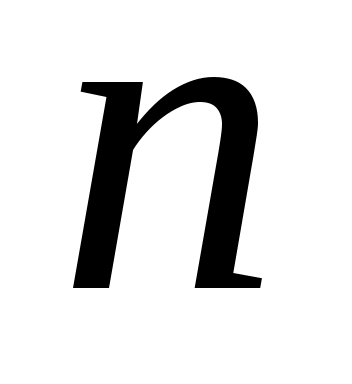 - теріс сан емес сандар берілсе, онда төмендегідей шамаларды енгіземіз. Олар:
- теріс сан емес сандар берілсе, онда төмендегідей шамаларды енгіземіз. Олар:
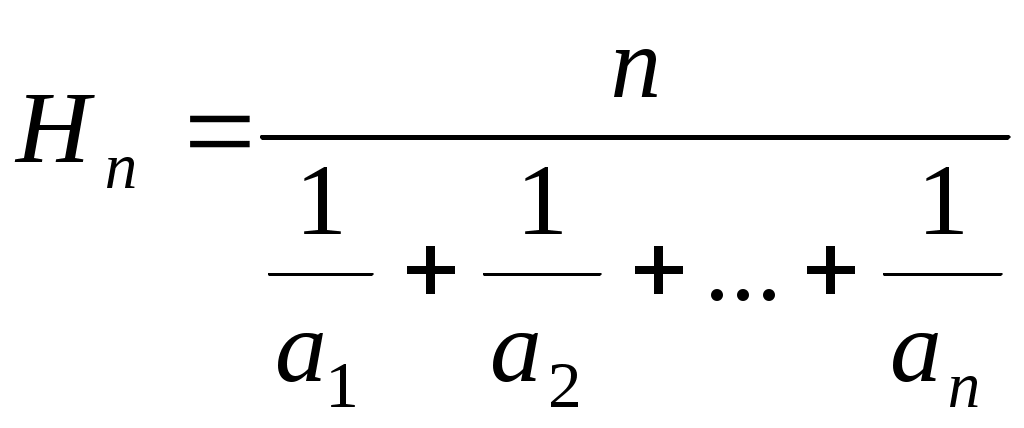 - гармониялық орта,
- гармониялық орта,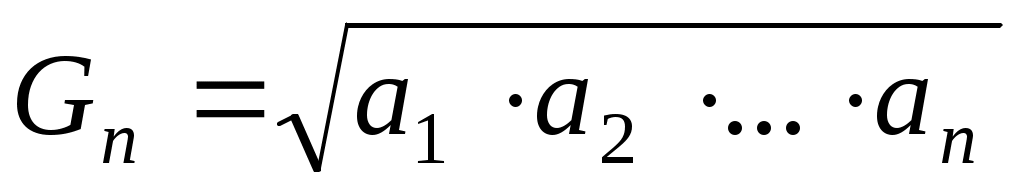 - геометриялық орта,
- геометриялық орта, 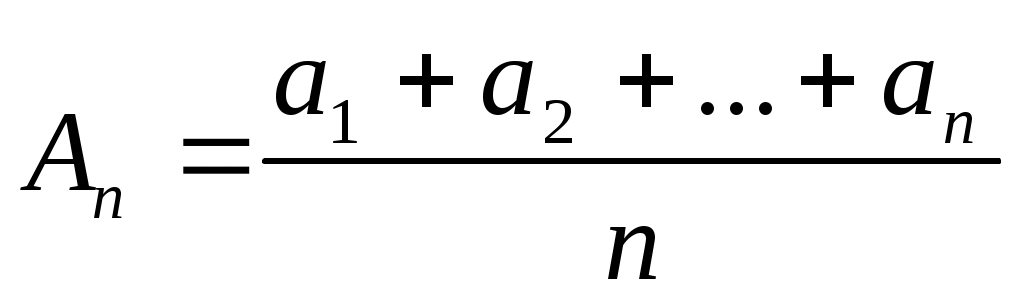 - арифметикалық орта,
- арифметикалық орта,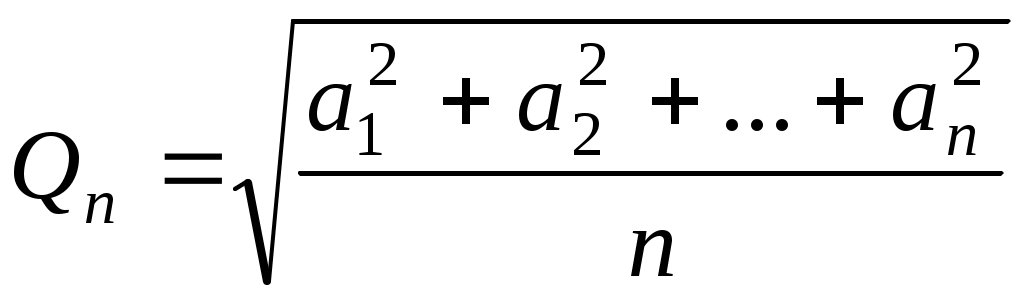 - квадраттық орта.
- квадраттық орта.
Осы орталар арасында келесі байланыстар: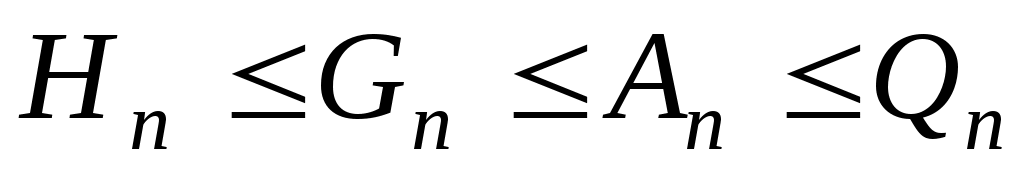 да қолданылады.
да қолданылады.
Студенттер математикалық индукция әдісін қолданып, теңсіздікті дәлелдеуге төмендегідей мысалдар келтірді.
1 Мыса.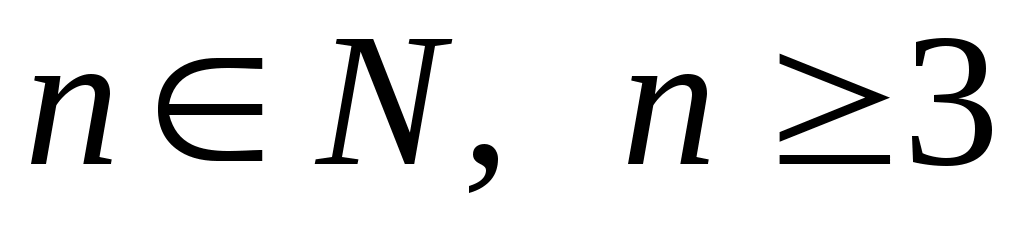 болса,
болса, 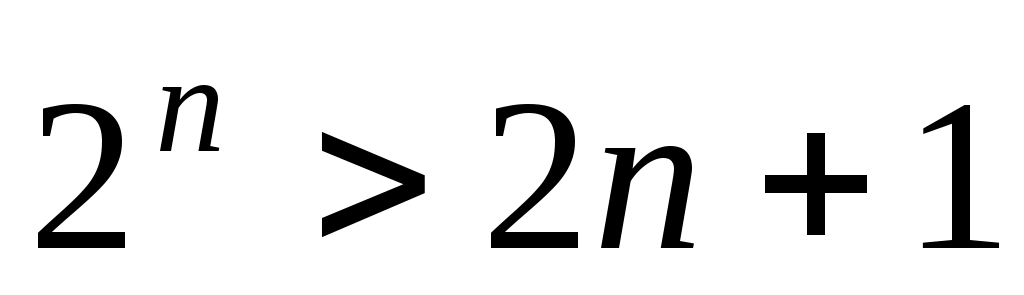 дәлелденуі.
дәлелденуі.
Дәлелдеуі.
1)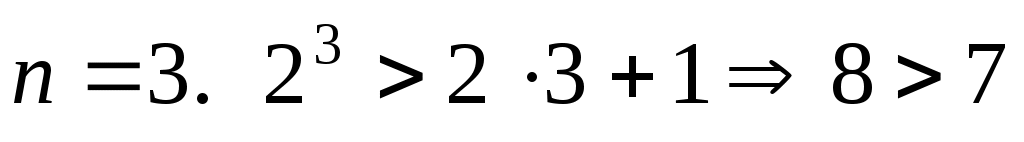 дұрыс;
дұрыс;
2)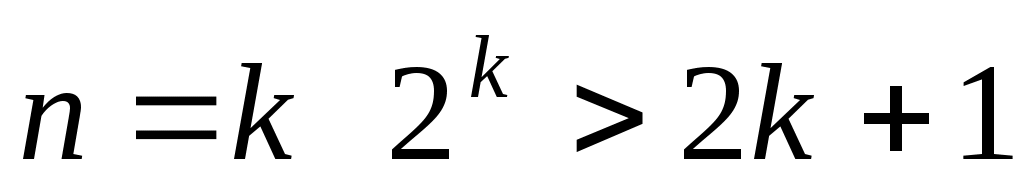 дұрыс деп санаймыз;
дұрыс деп санаймыз;
3)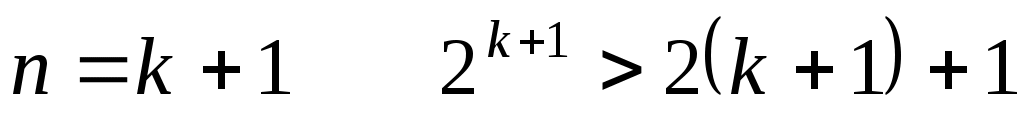 дұрыстығын дәлелдейік, яғни
дұрыстығын дәлелдейік, яғни 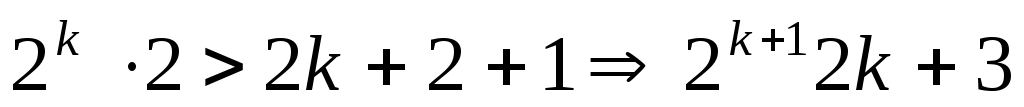
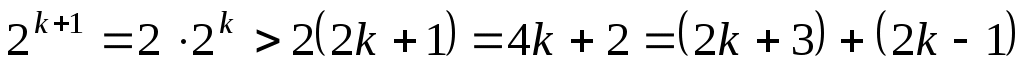
Олай болса,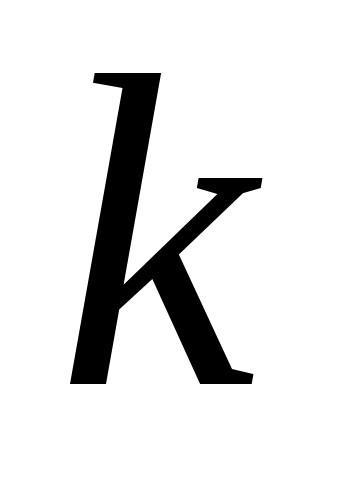 -ның кез келген мәнінде
-ның кез келген мәнінде 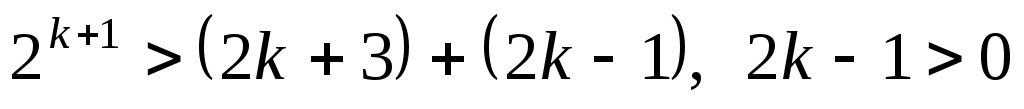 . Осылайша
. Осылайша 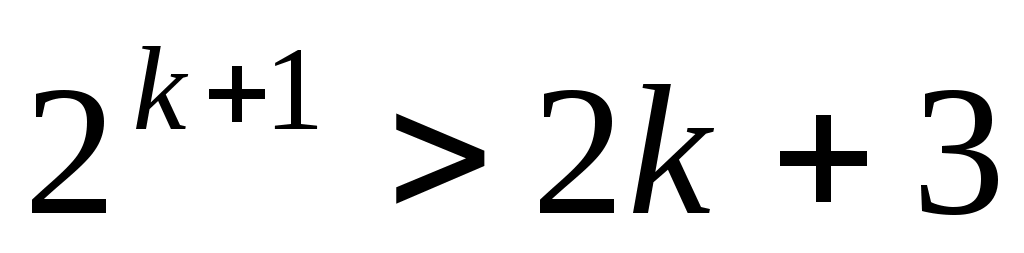 теңсіздігі дәлелденді деп есептейміз.
теңсіздігі дәлелденді деп есептейміз.
1.2 Теңсіздіктерді дәлелдеу
Теңдуелерді зерттеу ,жуық есептеу, иррационал сандар теориясы,сан қатарлары т.б. теңсіздіктер қасиетіне сүйенеді. Жоғарғы мектептегі математикалық анализ курсында функциялардың максимум және минимум яғни экстримал есептерді шешуде теңсіздіктер кең түрде қолданылады.
Тек математикада ғана емес әр түрлі жаратылыстану ғылымдарында зерттелетін табиғаттың үздіксіз процестері әсіресе экологиялық, экономикалық т.б. халық шаруашылығындағы балайланыстар теңсіздіктің көмегімен шешіледі. Теңсіздіктер оқушыларды айқын және дұрыс ойлауға, шамаларды салыстыра білуге дағдыландырады.
Әр түрлі теңсіздіктер ерте заманда-ақ белгілі болған.Эвклит пен Архимед шығармаларында көптеген теңсіздіктер келтірілген.Осы күнгі теңсіздіктер таңбасы ХVІІІ ғасырда ағылшын ғалымы Томас Гариаттың латын тілінде жазылған «Аналитикалық өнердің практикасы атты еңбегінде» тұнғыш рет келтіріледі.Теңдіктер теңсіздіктен жасалады,оларды теңсіздіктердің дербес бір түрі деуге болады.Теңсіздікті теңдікке айналдыру үшін екі шаманың айырмасын дәл бағалау керек.Теңсіздіктер жай санды теңсіздіктер,алгебралық теңсіздіктер,классикалық теңсіздіктер болып бөлінеді.Теңсіздікті дәлелдегенде және шешкенде тек әріптер мен белгісіз шамалардың мүмкін мәндерін үнемі есепке алу керек.Мысалы:таңбасы белгісіздің мүмкін мәндерінің кейбіреуінде ғана сақталатын теңсіздікті шартты немесе белгісізі бар теңсіздік деп атайды.барлық теңсіздіктердің қасиеттерін тек санды теңсіздіктер арқылы көрсетуге болады
1.аa теңсіздігі туады
2. а
Бұл қасиет теңсіздікті шешкенде,теоремалар дәлелдегенде теңсіздікті «күшейту» үшін қолданылады.
3. а
Теңсіздікті шешкенде, кейде ықшамдау мақсатымен оның екі бөлігінеде немесе екі бөлігінен де бірдей санды қосады немесе шегереді.
4.а-с
Бұл қасиет бойынша теңсіздік мүшелерінең таңбасын өзгерте отырып,бір бөлігінен екінші бөлігіне көшіруге болады.
5. а
Шарт бойынша а-b<0 және c-d<0.Екі теріс санның қосындысы да теріс.
Теңсіздіктің дәлелдеу жолының белгілі бір алгоритмін анықтау қиын. Бірақ оған қарамастан теңсіздікті қандайда бір айқын теңсіздікке түрлендіру жолы бар екенін айта кеткен жөн. Содан кейін айқын теңсіздікті логикалық талдау арқылы берілген теңсіздікті келтіруге болады.
Негізгі теңсіздіктер: 1. а+в≥√ав, а≥0, в≥0
2.а+в≥2,(а мен в-ның таңбасы бірдей);
в а
3. 1:1(1+1)≤√ав, а>0, в>0,
2 а в
Гармониялық орта;
4. 2ав≤√ав≤ а+в;
а+в 2
5. ׀а+в׀≤ ׀а׀ +׀ в׀ тек а•в≥0 болғанда орындалады
Теңсіздіктерді дәлелдеу әдістері;
1. Анықтама бойынша, яғни анықтамаға сүйеніп дәлелдеу. Мысалы,
а5-в5 ≥ а4в-ав4, мұндағы а > в
Дәлелдеу: а5-в5-а4в+ав4=а4(а-в)+в4(а-в) =(а-в)(а4+в4) ≥0
2. Дәлелденген теңсіздік көмегімен;
а>0, в>0, с>0, d>0
(1+вс)(1+cd)(1+ cd)(1+ав) ≥16
ad aв вс cd
Дәлелдеу:
Каши теңсіздігін қолданамыз
1+вс≥2√вс
ad ad
1+сd≥2√cd }→(1+вс)(1+сd)(1+ ad)
ad aв ad aв вс
(1+ав) ≥16 √вс•сd•ad•ав=16
cd ad ad вс cd
1+ad≥2√ad
вс вс
1+ав≥2√ad
сd сd
3. Талдау арқылы дәлелдеу
4. Кері жору арқылы ділелдеу
5. Геометриялық тәсіл
6. Теңсіздікті «күшейту» тәсілі
7. Графиктік тәсіл
8. Сызықтық программалау, симплекс, математикалық индукция
9. Реттелген жиындар әдісі
Теңсіздіктің түрлері:
1. Кейбір теңсіздіктер белгілі бір сандардың шамаларының әр түрлі орташаларына тәуелді болады. Бұл шамалар Hn≤Gn≤An≤Qn
An – арифметикалық орташа
Gn – геометриялық орташа
Qn – квадраттық орташа
Hn – гармониялық орташа
1. a1+a2+….+an≥√a1a2……..an
n
a1a2…an сандарының арифметикалық орташасы , олардың геометриялық орташасынан аз емес. Бұл теңсіздікті француз математигі О.Каши 1821 жылы жариялағаг болатын.
2. Гюйгенс теңсіздігі
3. Чебышев теңсіздігі
4. Коши – Буняковский теңсіздігі
5. Бернулли теңсіздігі
6. Гельдер теңсіздігі
0>
2. Теңсіздіктерді дәлелдеу әдістері
2.1 Қарапайым теңсіздіктерді Штурм әдісін қолданып дәлелдеу
Мектеп көлемінде қарапайым теңсіздіктер дәлелденеді, сол теңсіздіктер арқылы күрделі теңсіздіктерде дәлелденеді.
№1 а2 + b2 ≥ 2ab.
Дәлелдеуі:
a2+ b2 - 2аb = (а – b)2 ≥ 0.
№2
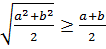 кез келген a және b үшін.
кез келген a және b үшін.
Дәлелдеуі:
Берілген теңсіздіктен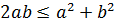 , біз мына теңсіздікті аламыз
, біз мына теңсіздікті аламыз 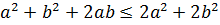 бұдан
бұдан 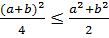 немесе
немесе 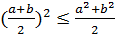 соны мына түрде жазамыз
соны мына түрде жазамыз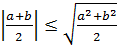 бұдан
бұдан 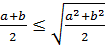
Штурм әдісін қолданып теңсіздікті дәлелдеу
Бұл әдісті неміс математигі Р.Штурм ұсынған. Бұл әдістің көмегімен бірнеше теңсіздікті дәлелдейік:
№3 Егер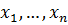 қосындысы 1-ге тең болса, онда
қосындысы 1-ге тең болса, онда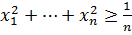 дәлелдеу керек
дәлелдеу керек
Дәлелдеуі:
Егер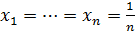 онда
онда 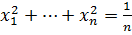 .
.
Қаралатын сандардың ішінде ең болмағанда екі сан бір-біріне тең болмаса, онда сандардың ішінен екі сан табылады, сонын біреуі - нан үлкен болады, ал екіншісі кіші болады. Осы сандар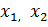 болсын, және де
болсын, және де 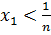
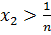 болсын, онда - ді -ні
болсын, онда - ді -ні 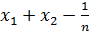
- мен алмастырып, мынандай теңсіздік аламыз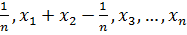 және олардың қосындысы 1-ге тең.
және олардың қосындысы 1-ге тең.
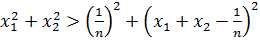 болғандықтан, осыдан
болғандықтан, осыдан
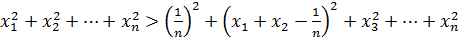 .
.
Осы амалды бірнеше рет қайталап, шыққан тізбектің кез келген мүшесі -ге тең, ал олардың квадраттарының қосындысы берілген сандардың квадраттарының қосындысынан кіші болады.
сандардың квадраттарының қосындысынан кіші болады.
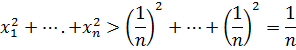
2.2 Арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолдану әдісі
Кейбір теңсіздіктерді дәлелдегенде, оң a және b сандары үшін арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолданады: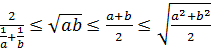 .
.
Мына өрнекте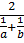 гармониялық орта,
гармониялық орта,
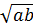 – геометриялық орта,
– геометриялық орта,
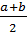 – арифметикалық орта,
– арифметикалық орта,
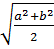 – квадраттық орта.
– квадраттық орта.
Бұл теңсіздікті дәлелдеу әдісі күрделі теңсіздіктерді дәлелдеуде көп қолданылады.
№4 теңсіздікті дәлелде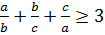 , мұндағы
, мұндағы 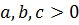
Дәлелдеуі: егер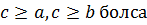 , онда
, онда 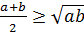 - ны қолданып,
- ны қолданып,
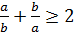
-ны (1) аламыз және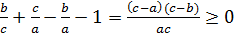 осыдан
осыдан 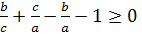 (2)
(2)
(1) және (2) қосып аламыз.
аламыз.
2.3 Коши-Буняковский әдісін қолдану
Коши-Буняковский әдісін бірінші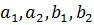 сандар үшін дәлелдейміз.
сандар үшін дәлелдейміз. 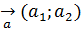 және
және 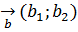 векторлары берілсін, мектеп көлемінде белгілі
векторлары берілсін, мектеп көлемінде белгілі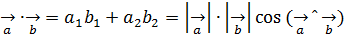
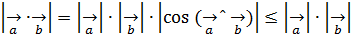
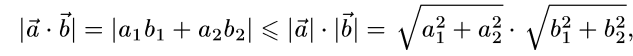
немесе
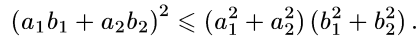
Бұл Коши-Буняковскийдің теңсіздігі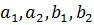 сандары үшін орындалатын дербес жағдайы болады.
сандары үшін орындалатын дербес жағдайы болады.
Коши-Буняковскийдің теңсіздігі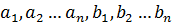 сандары үшін келесі жалпы түрде жазылады:
сандары үшін келесі жалпы түрде жазылады:
№5. Дәлелдеу керек :
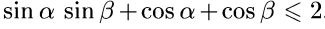
Дәлелдеуі:
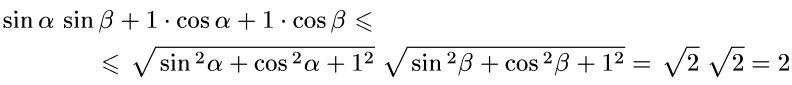
2.4 Жаңа айнымалы енгізу әдісі
Кейбір теңсіздіктерді дәлелдеу үшін жаңа айнымалы енгізу арқылы мақсатқа жетуге болады.
№6. Теңсіздікті дәлелде
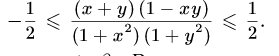
Дәлелдеуі:
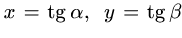
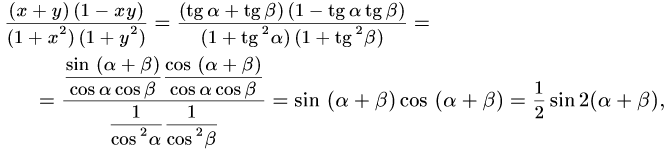
Теңсіздіктерді осы сияқты дәлелдеу үшін
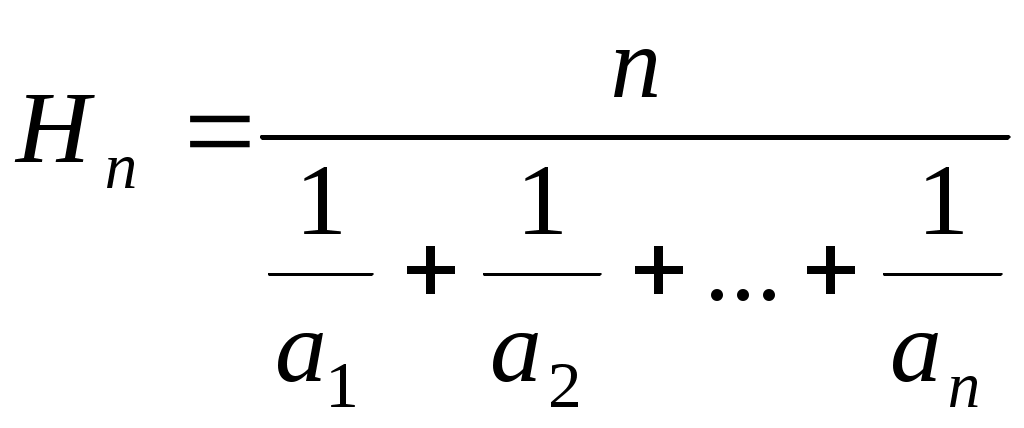 - гармониялық орта,
- гармониялық орта,Осы орталар арасында келесі байланыстар:
Студенттер математикалық индукция әдісін қолданып, теңсіздікті дәлелдеуге төмендегідей мысалдар келтірді.
1 Мыса.
Дәлелдеуі.
1)
2)
3)
Олай болса,
1.2 Теңсіздіктерді дәлелдеу
Теңдуелерді зерттеу ,жуық есептеу, иррационал сандар теориясы,сан қатарлары т.б. теңсіздіктер қасиетіне сүйенеді. Жоғарғы мектептегі математикалық анализ курсында функциялардың максимум және минимум яғни экстримал есептерді шешуде теңсіздіктер кең түрде қолданылады.
Тек математикада ғана емес әр түрлі жаратылыстану ғылымдарында зерттелетін табиғаттың үздіксіз процестері әсіресе экологиялық, экономикалық т.б. халық шаруашылығындағы балайланыстар теңсіздіктің көмегімен шешіледі. Теңсіздіктер оқушыларды айқын және дұрыс ойлауға, шамаларды салыстыра білуге дағдыландырады.
Әр түрлі теңсіздіктер ерте заманда-ақ белгілі болған.Эвклит пен Архимед шығармаларында көптеген теңсіздіктер келтірілген.Осы күнгі теңсіздіктер таңбасы ХVІІІ ғасырда ағылшын ғалымы Томас Гариаттың латын тілінде жазылған «Аналитикалық өнердің практикасы атты еңбегінде» тұнғыш рет келтіріледі.Теңдіктер теңсіздіктен жасалады,оларды теңсіздіктердің дербес бір түрі деуге болады.Теңсіздікті теңдікке айналдыру үшін екі шаманың айырмасын дәл бағалау керек.Теңсіздіктер жай санды теңсіздіктер,алгебралық теңсіздіктер,классикалық теңсіздіктер болып бөлінеді.Теңсіздікті дәлелдегенде және шешкенде тек әріптер мен белгісіз шамалардың мүмкін мәндерін үнемі есепке алу керек.Мысалы:таңбасы белгісіздің мүмкін мәндерінің кейбіреуінде ғана сақталатын теңсіздікті шартты немесе белгісізі бар теңсіздік деп атайды.барлық теңсіздіктердің қасиеттерін тек санды теңсіздіктер арқылы көрсетуге болады
1.аa теңсіздігі туады
2. а
Бұл қасиет теңсіздікті шешкенде,теоремалар дәлелдегенде теңсіздікті «күшейту» үшін қолданылады.
3. а
Теңсіздікті шешкенде, кейде ықшамдау мақсатымен оның екі бөлігінеде немесе екі бөлігінен де бірдей санды қосады немесе шегереді.
4.а-с
Бұл қасиет бойынша теңсіздік мүшелерінең таңбасын өзгерте отырып,бір бөлігінен екінші бөлігіне көшіруге болады.
5. а
Шарт бойынша а-b<0 және c-d<0.Екі теріс санның қосындысы да теріс.
Теңсіздіктің дәлелдеу жолының белгілі бір алгоритмін анықтау қиын. Бірақ оған қарамастан теңсіздікті қандайда бір айқын теңсіздікке түрлендіру жолы бар екенін айта кеткен жөн. Содан кейін айқын теңсіздікті логикалық талдау арқылы берілген теңсіздікті келтіруге болады.
Негізгі теңсіздіктер: 1. а+в≥√ав, а≥0, в≥0
2.а+в≥2,(а мен в-ның таңбасы бірдей);
в а
3. 1:1(1+1)≤√ав, а>0, в>0,
2 а в
Гармониялық орта;
4. 2ав≤√ав≤ а+в;
а+в 2
5. ׀а+в׀≤ ׀а׀ +׀ в׀ тек а•в≥0 болғанда орындалады
Теңсіздіктерді дәлелдеу әдістері;
1. Анықтама бойынша, яғни анықтамаға сүйеніп дәлелдеу. Мысалы,
а5-в5 ≥ а4в-ав4, мұндағы а > в
Дәлелдеу: а5-в5-а4в+ав4=а4(а-в)+в4(а-в) =(а-в)(а4+в4) ≥0
2. Дәлелденген теңсіздік көмегімен;
а>0, в>0, с>0, d>0
(1+вс)(1+cd)(1+ cd)(1+ав) ≥16
ad aв вс cd
Дәлелдеу:
Каши теңсіздігін қолданамыз
1+вс≥2√вс
ad ad
1+сd≥2√cd }→(1+вс)(1+сd)(1+ ad)
ad aв ad aв вс
(1+ав) ≥16 √вс•сd•ad•ав=16
cd ad ad вс cd
1+ad≥2√ad
вс вс
1+ав≥2√ad
сd сd
3. Талдау арқылы дәлелдеу
4. Кері жору арқылы ділелдеу
5. Геометриялық тәсіл
6. Теңсіздікті «күшейту» тәсілі
7. Графиктік тәсіл
8. Сызықтық программалау, симплекс, математикалық индукция
9. Реттелген жиындар әдісі
Теңсіздіктің түрлері:
1. Кейбір теңсіздіктер белгілі бір сандардың шамаларының әр түрлі орташаларына тәуелді болады. Бұл шамалар Hn≤Gn≤An≤Qn
An – арифметикалық орташа
Gn – геометриялық орташа
Qn – квадраттық орташа
Hn – гармониялық орташа
1. a1+a2+….+an≥√a1a2……..an
n
a1a2…an сандарының арифметикалық орташасы , олардың геометриялық орташасынан аз емес. Бұл теңсіздікті француз математигі О.Каши 1821 жылы жариялағаг болатын.
2. Гюйгенс теңсіздігі
3. Чебышев теңсіздігі
4. Коши – Буняковский теңсіздігі
5. Бернулли теңсіздігі
6. Гельдер теңсіздігі
0>
2. Теңсіздіктерді дәлелдеу әдістері
2.1 Қарапайым теңсіздіктерді Штурм әдісін қолданып дәлелдеу
Мектеп көлемінде қарапайым теңсіздіктер дәлелденеді, сол теңсіздіктер арқылы күрделі теңсіздіктерде дәлелденеді.
№1 а2 + b2 ≥ 2ab.
Дәлелдеуі:
a2+ b2 - 2аb = (а – b)2 ≥ 0.
№2
Дәлелдеуі:
Берілген теңсіздіктен
Штурм әдісін қолданып теңсіздікті дәлелдеу
Бұл әдісті неміс математигі Р.Штурм ұсынған. Бұл әдістің көмегімен бірнеше теңсіздікті дәлелдейік:
№3 Егер
Дәлелдеуі:
Егер
Қаралатын сандардың ішінде ең болмағанда екі сан бір-біріне тең болмаса, онда сандардың ішінен екі сан табылады, сонын біреуі - нан үлкен болады, ал екіншісі кіші болады. Осы сандар
- мен алмастырып, мынандай теңсіздік аламыз
Осы амалды бірнеше рет қайталап, шыққан тізбектің кез келген мүшесі -ге тең, ал олардың квадраттарының қосындысы берілген
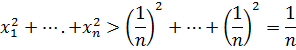
2.2 Арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолдану әдісі
Кейбір теңсіздіктерді дәлелдегенде, оң a және b сандары үшін арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолданады:
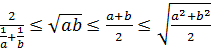 .
.Мына өрнекте
Бұл теңсіздікті дәлелдеу әдісі күрделі теңсіздіктерді дәлелдеуде көп қолданылады.
№4 теңсіздікті дәлелде
Дәлелдеуі: егер
-ны (1) аламыз және
(1) және (2) қосып
2.3 Коши-Буняковский әдісін қолдану
Коши-Буняковский әдісін бірінші
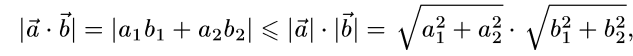
немесе
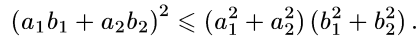
Бұл Коши-Буняковскийдің теңсіздігі
Коши-Буняковскийдің теңсіздігі
№5. Дәлелдеу керек :
Дәлелдеуі:
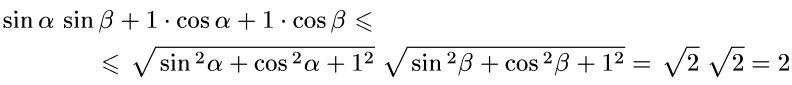
2.4 Жаңа айнымалы енгізу әдісі
Кейбір теңсіздіктерді дәлелдеу үшін жаңа айнымалы енгізу арқылы мақсатқа жетуге болады.
№6. Теңсіздікті дәлелде
Дәлелдеуі: