ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 120
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
>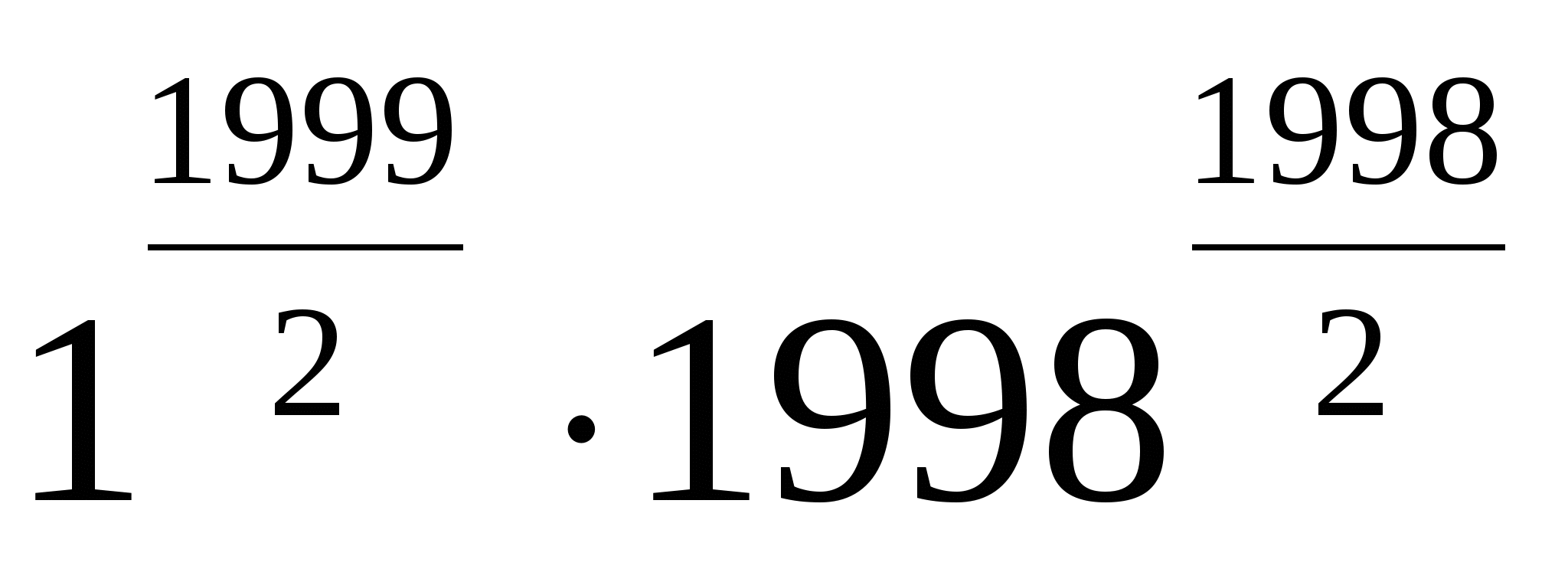 ;
;
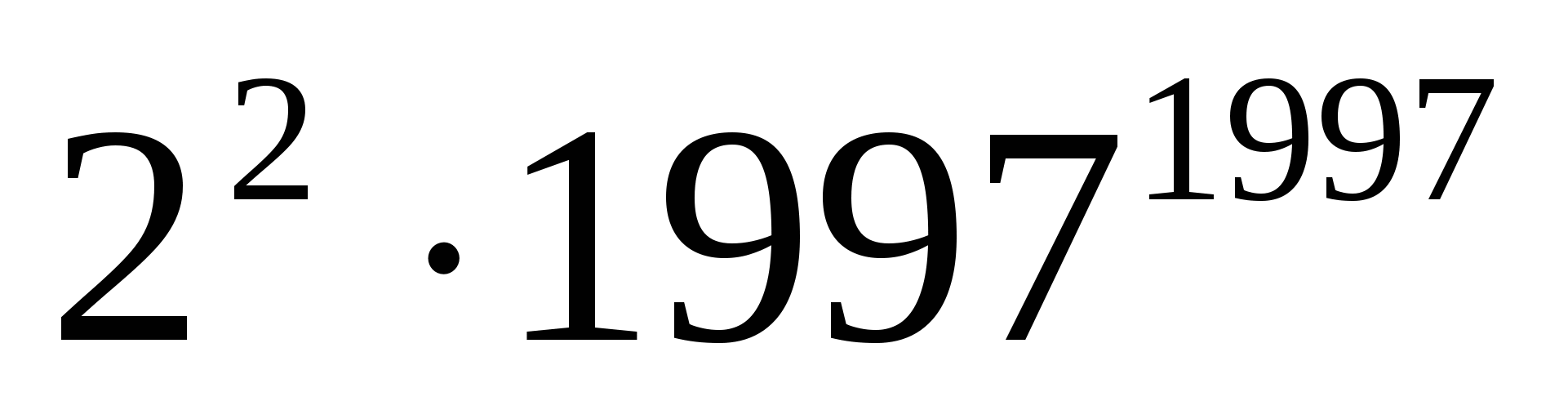 >
>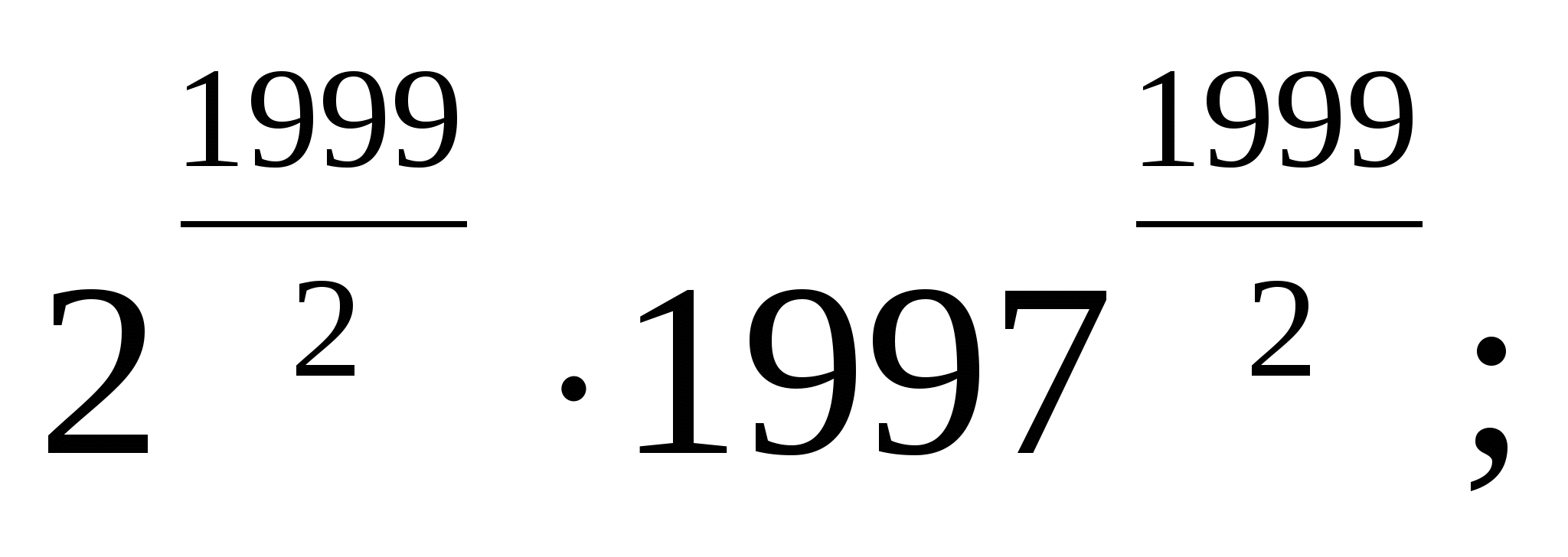 ...
... 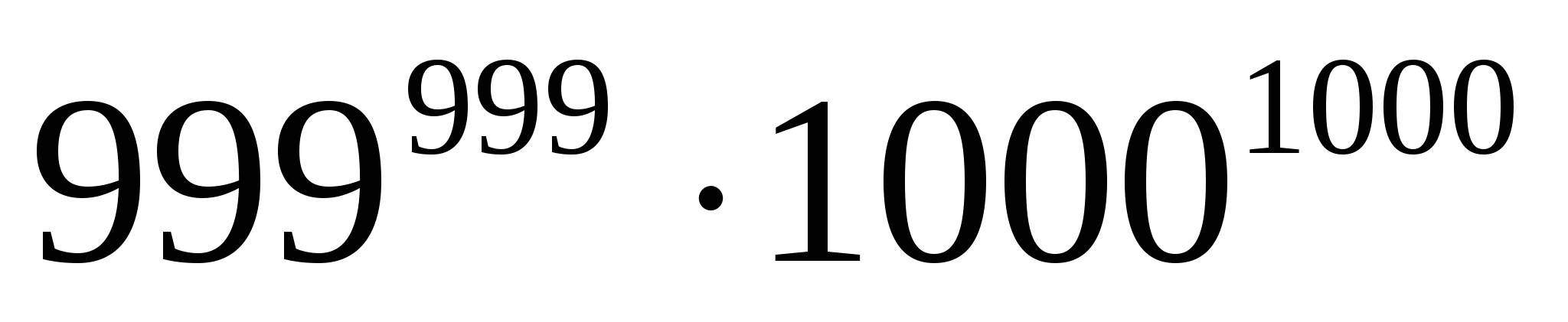
 >
>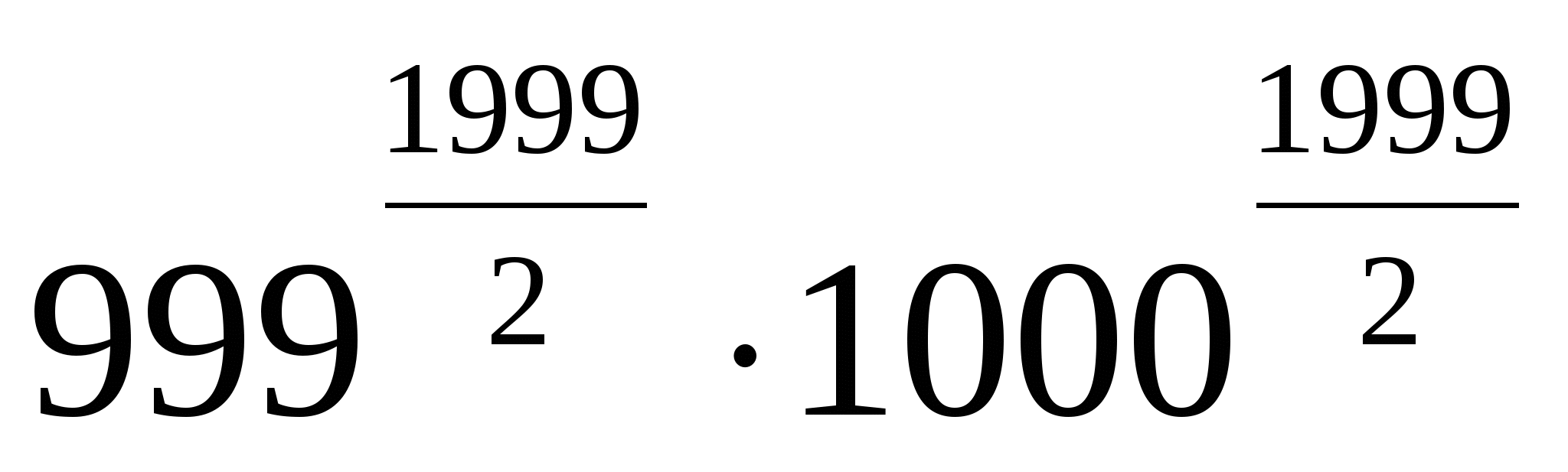
 Бұл теңсіздіктерді мүшелеп көбейтіп, дәлелденілген теңсіздікке келеміз.
Бұл теңсіздіктерді мүшелеп көбейтіп, дәлелденілген теңсіздікке келеміз.
9-сынып
№1. a>в>0 сандары үшін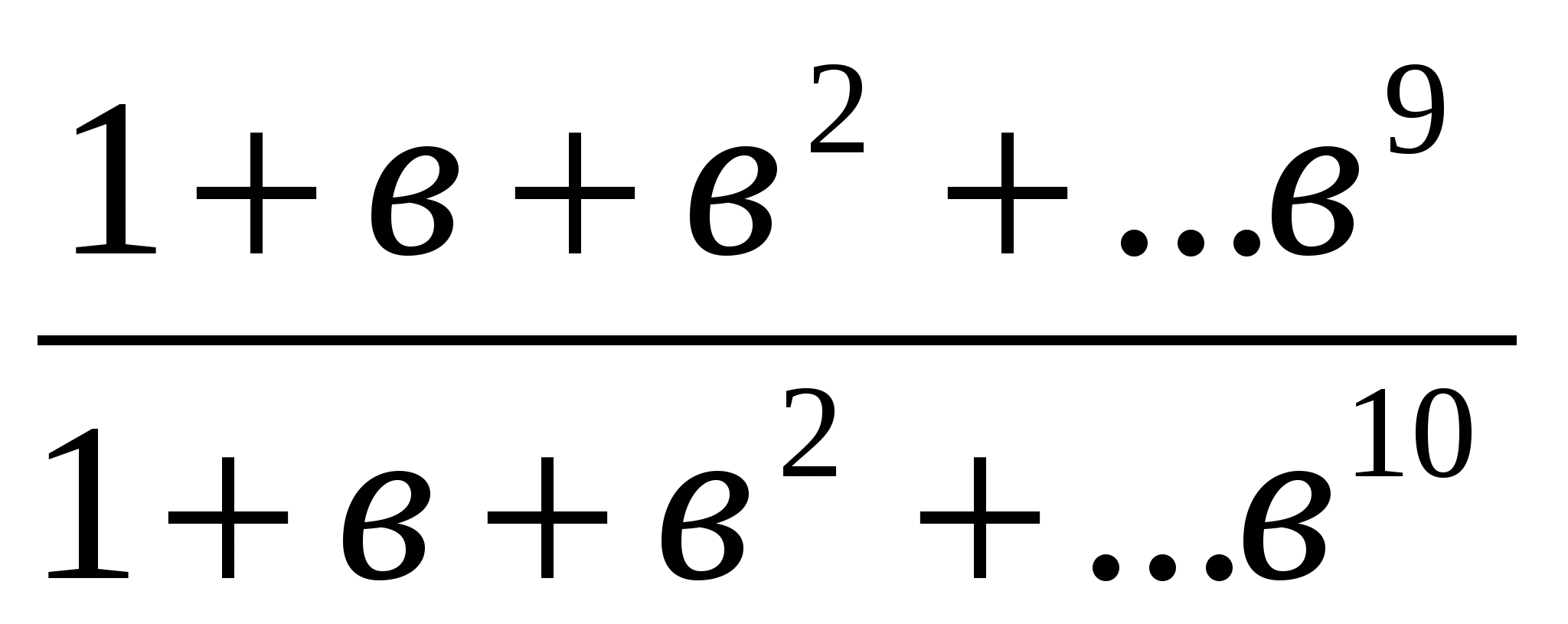 >
>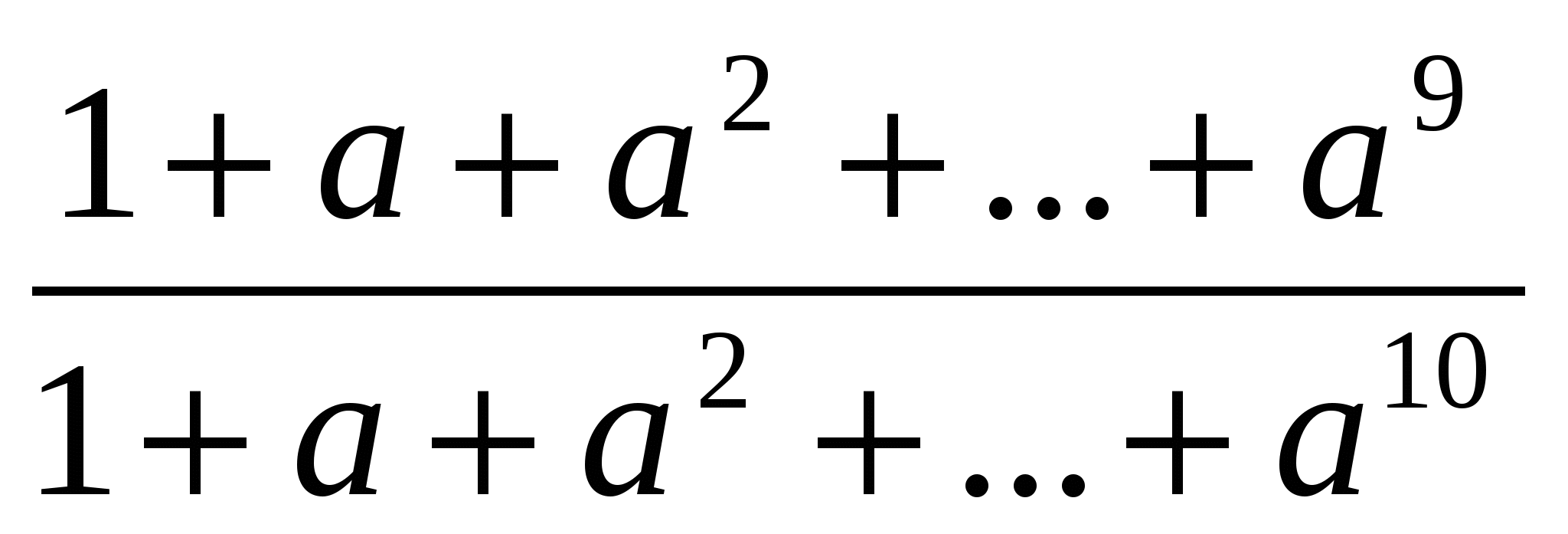 теңсіздігін дәлелдеңдер.
теңсіздігін дәлелдеңдер.
Дәлелдеуі: Дәлелденетін теңсіздік мынадай теңсіздікпен мәндес:
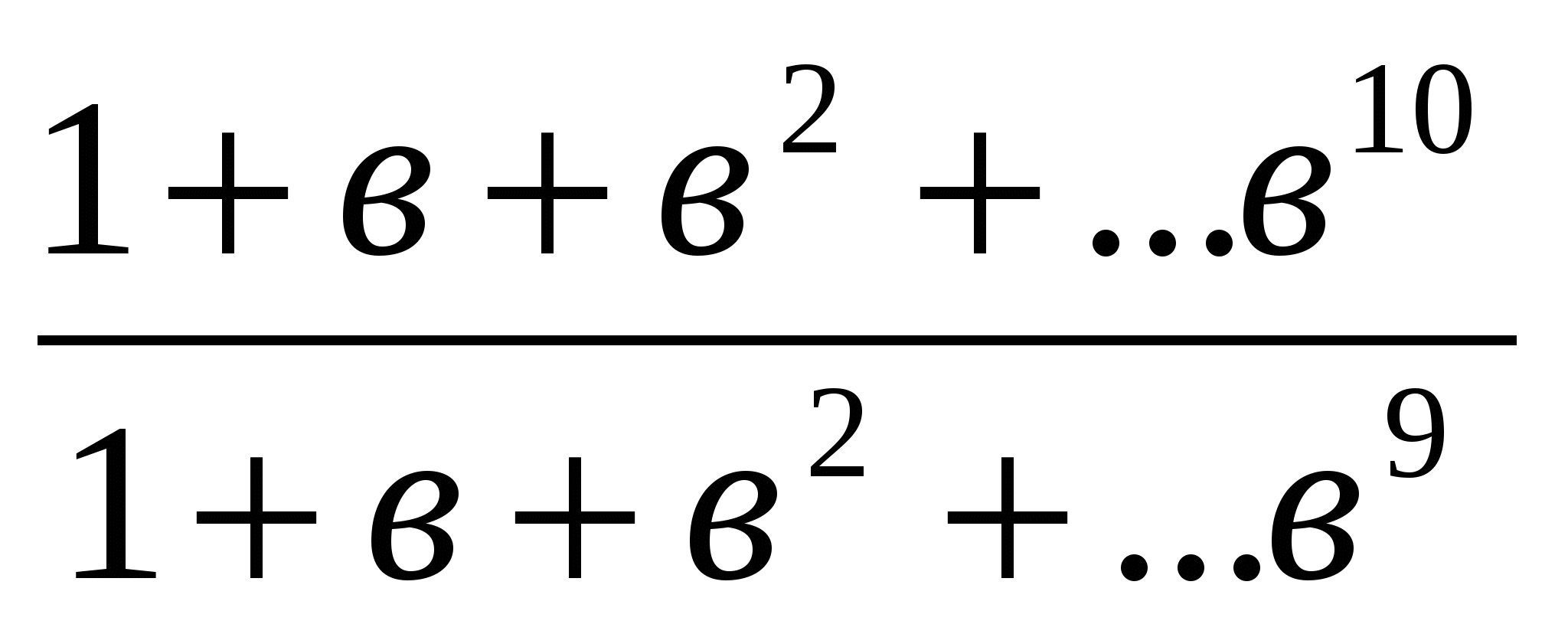 <
<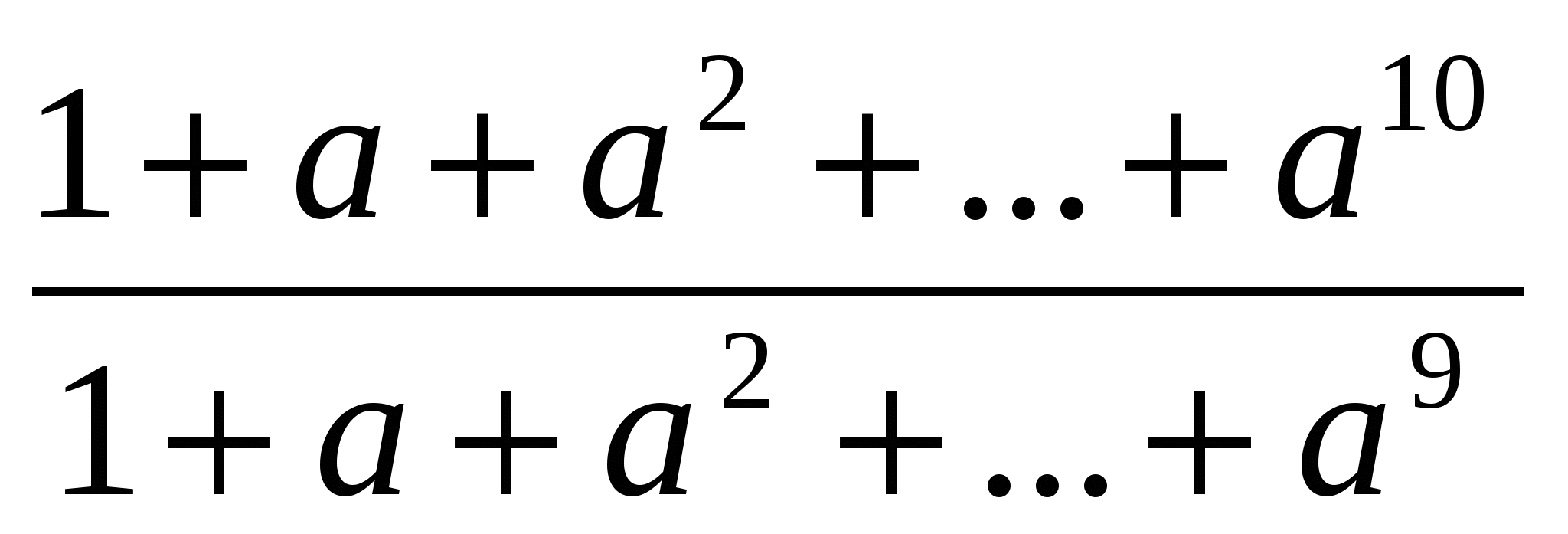
немесе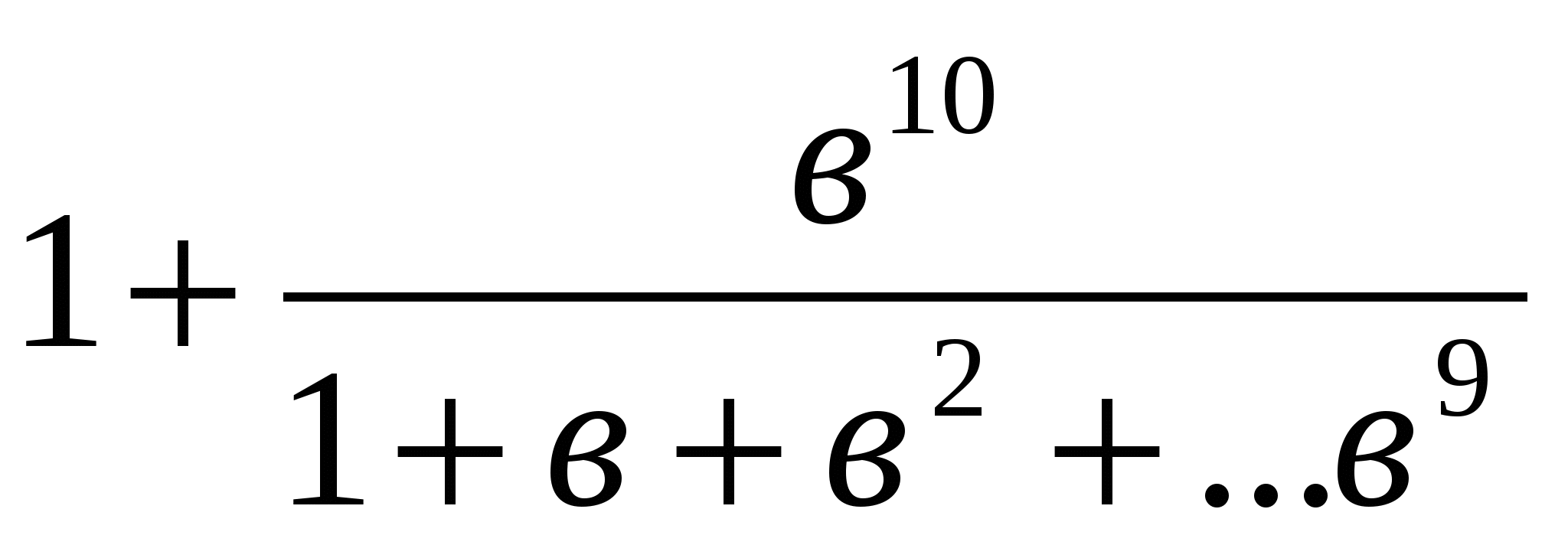 <
< 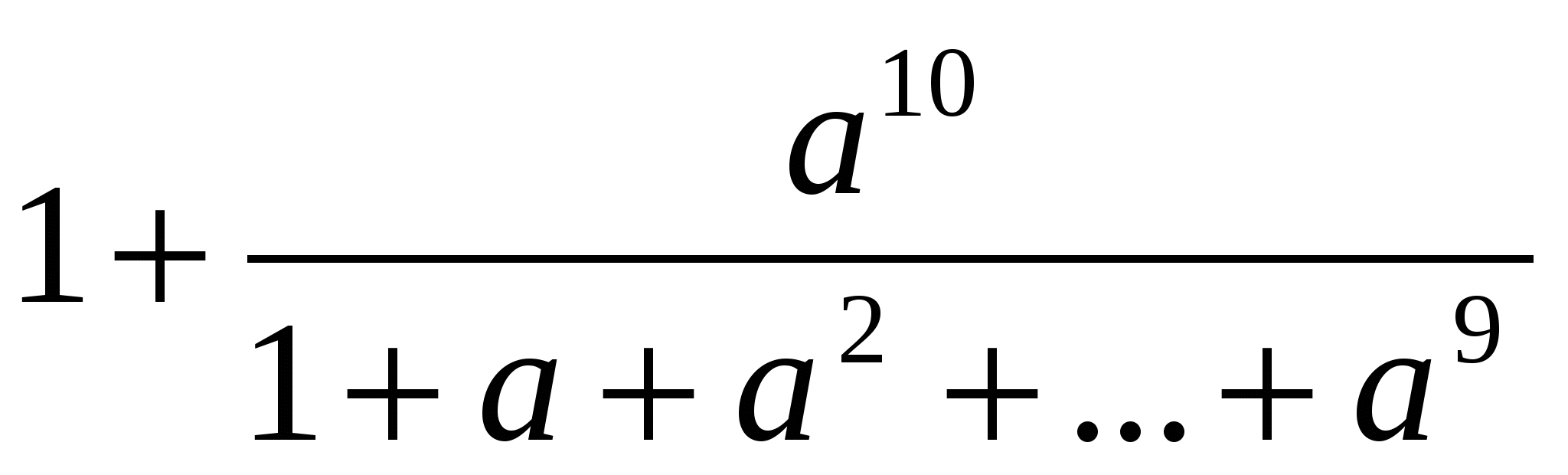
немесе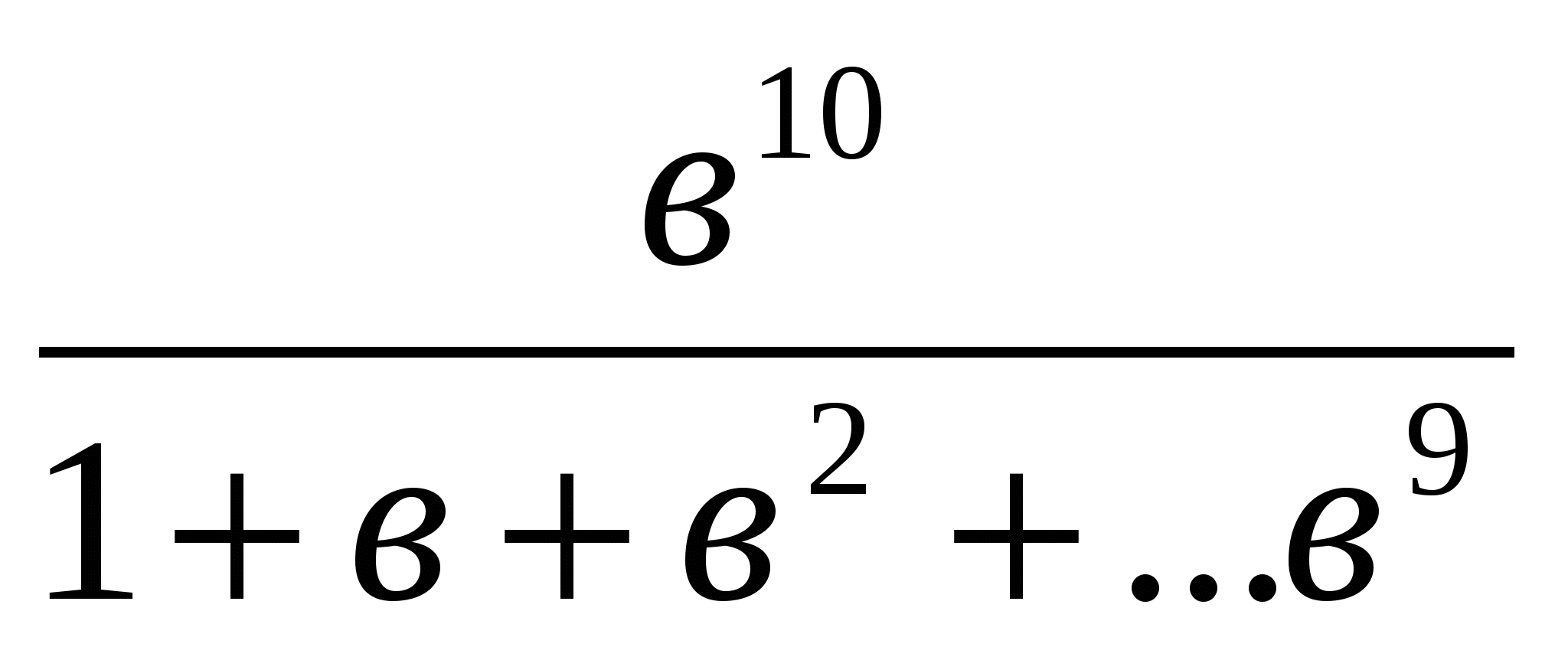 <
<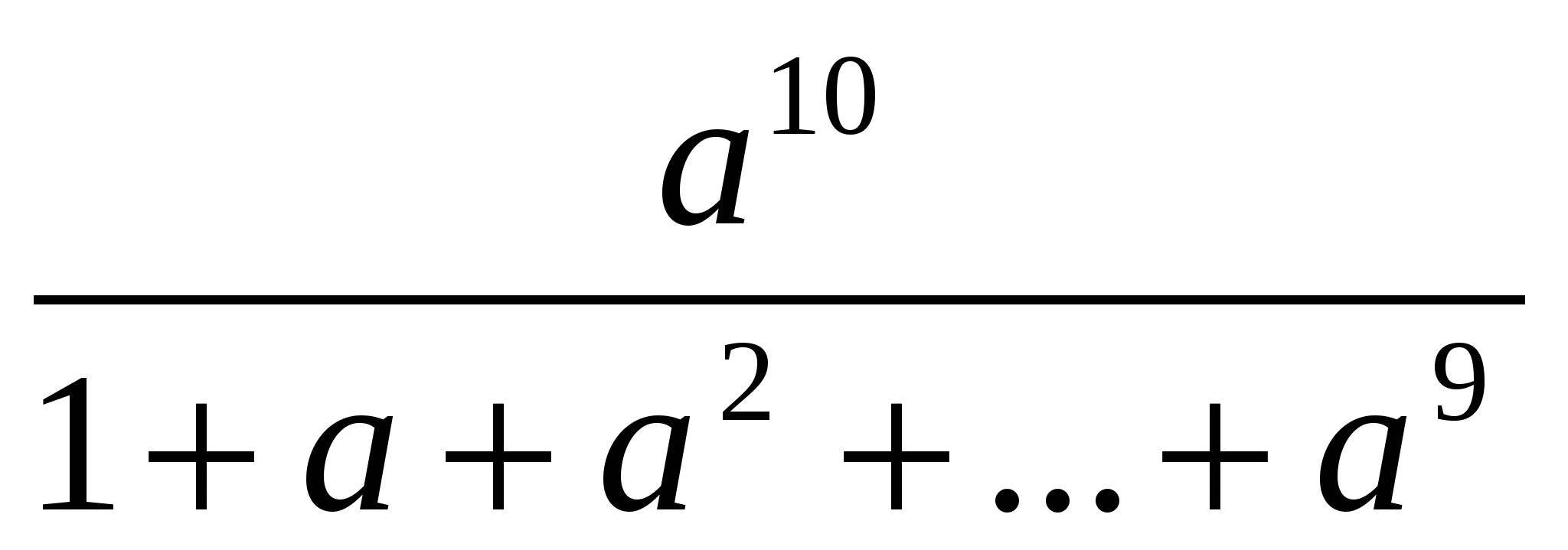
немесе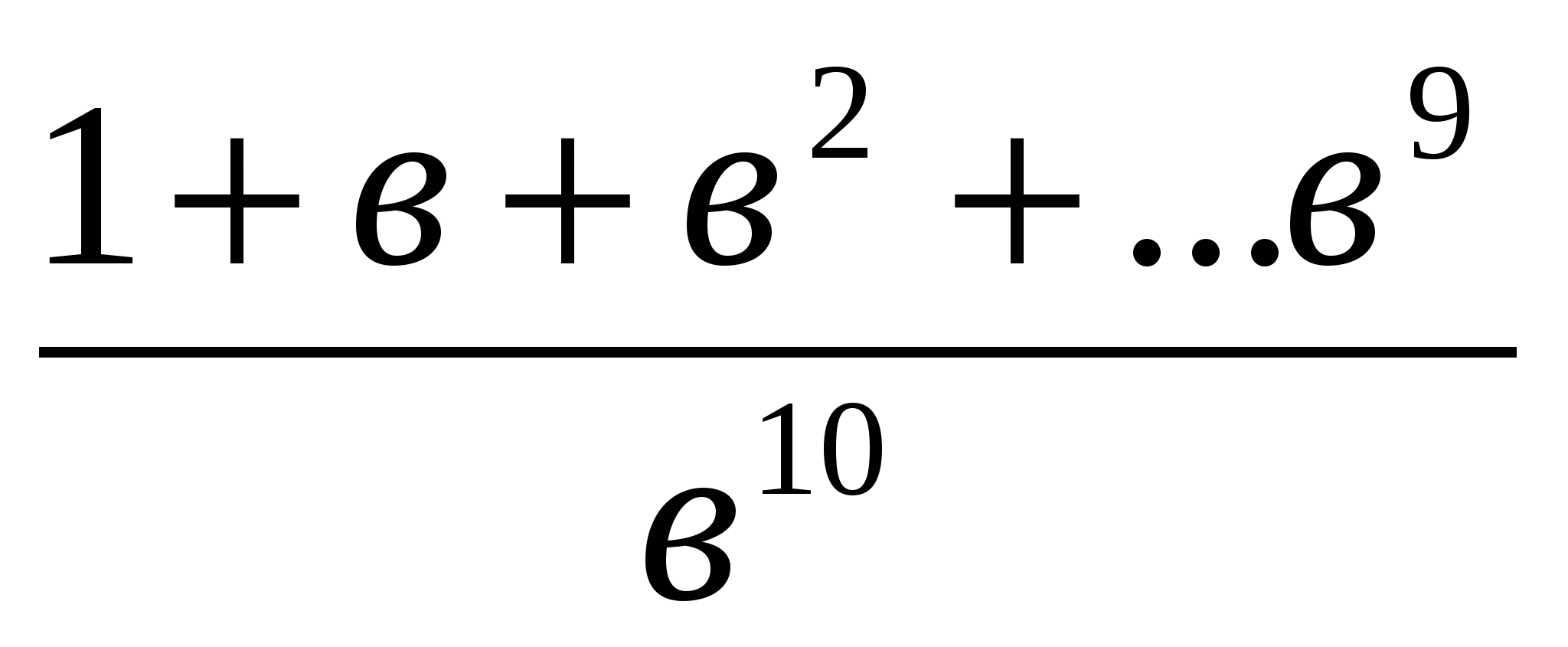 >
>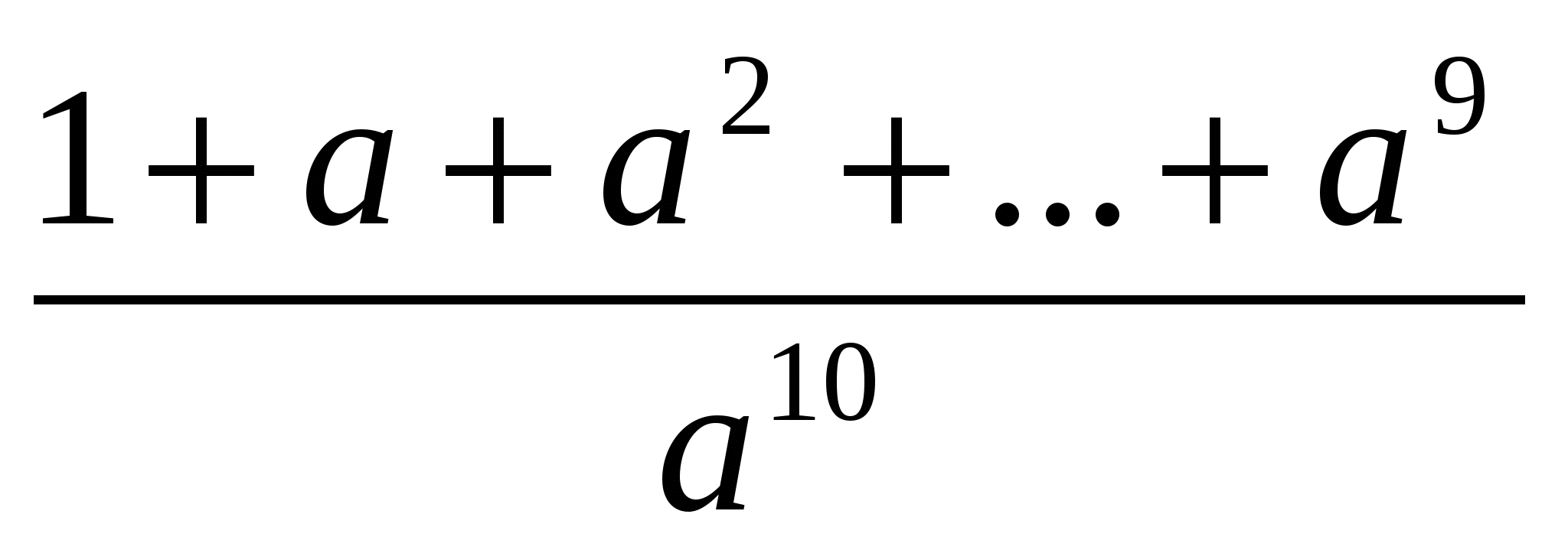
немесе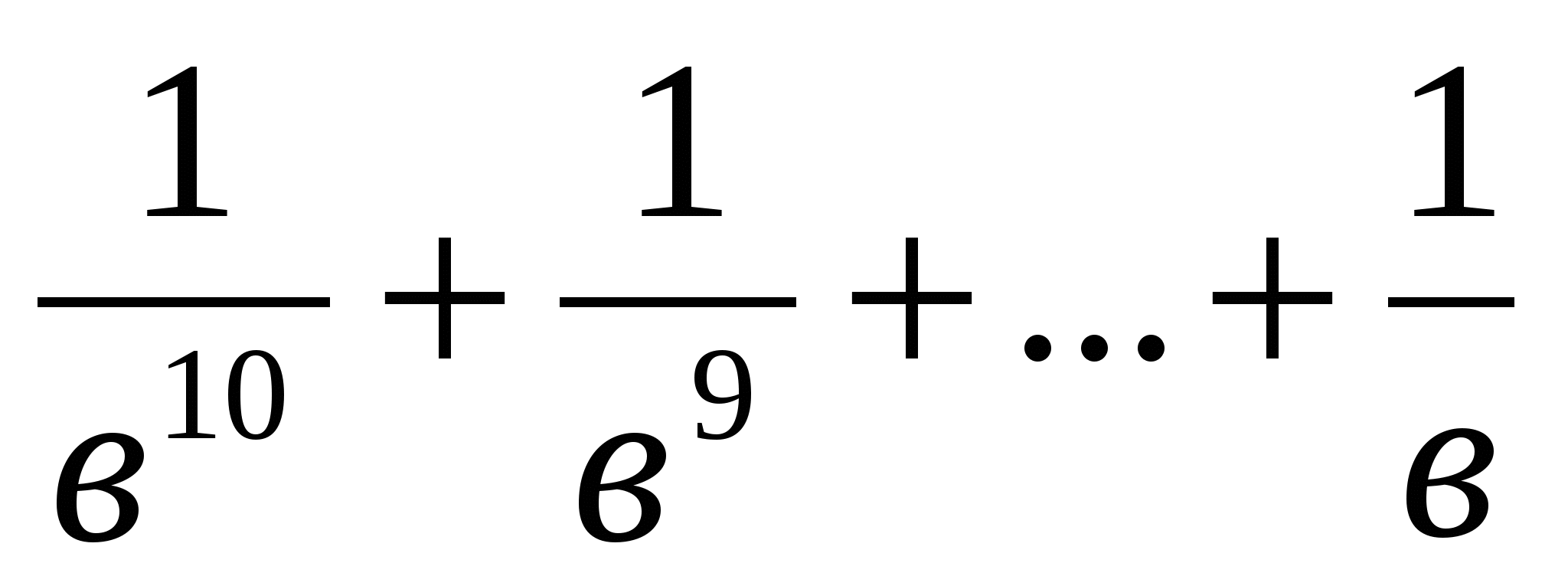 >
>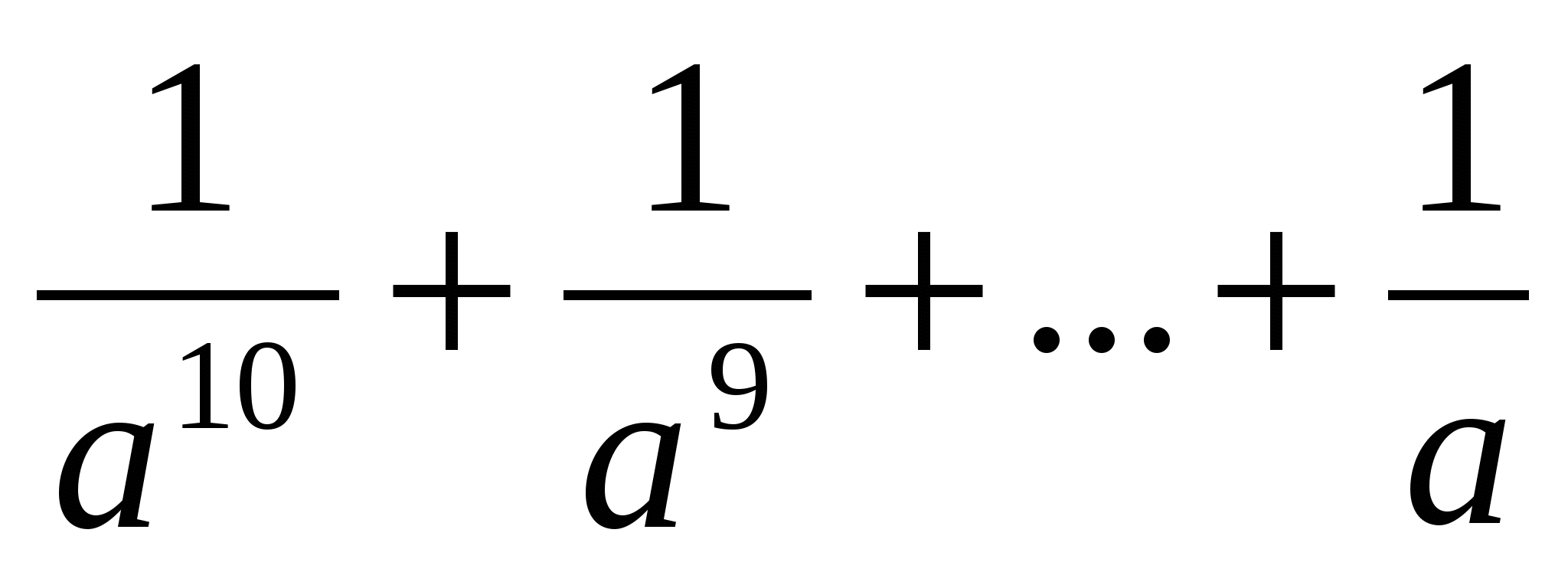
Соңғы теңсіздік тура болғандықтан дәлелденілетін теңсіздік те тура болады.
3.4 Республикалық олимпиада
11-сынып
№1.а+в+с=1, (a,в,с≥0) шарттарын қанағаттандыратын а,в,с сандары үшін теңсіздікті дәлелдеңіздер. (1+а)(1+в)(1+с)≥8(1-а)(1-в)(1-с).
Дәлелдеуі: 1+а=(1-в)+(1-с) онда 1+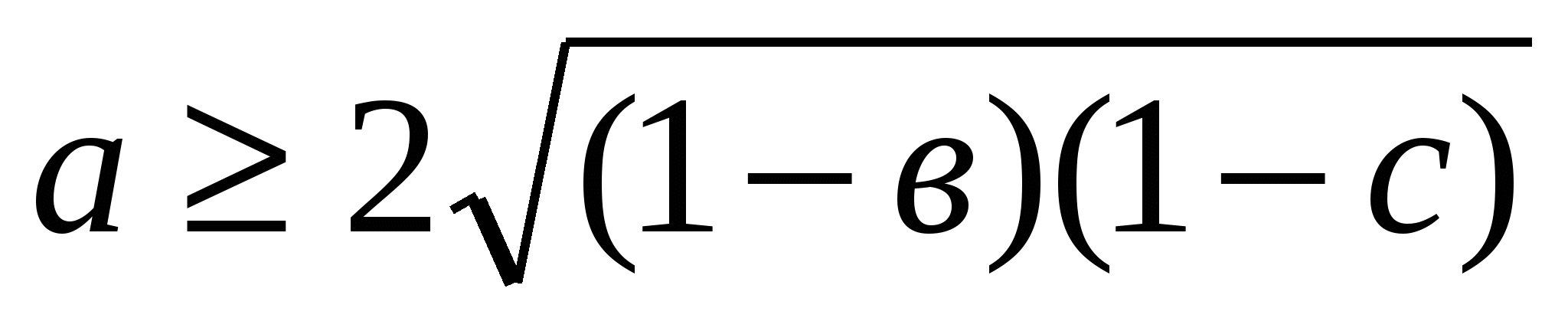 . Осы сияқты
. Осы сияқты 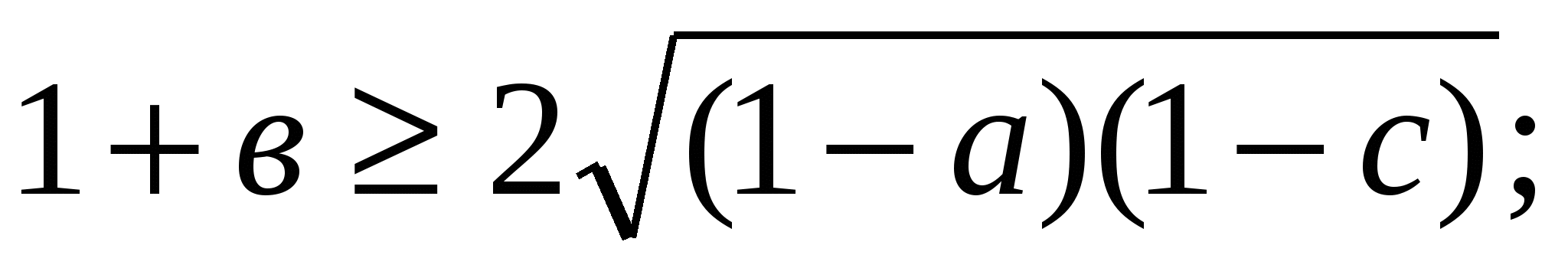
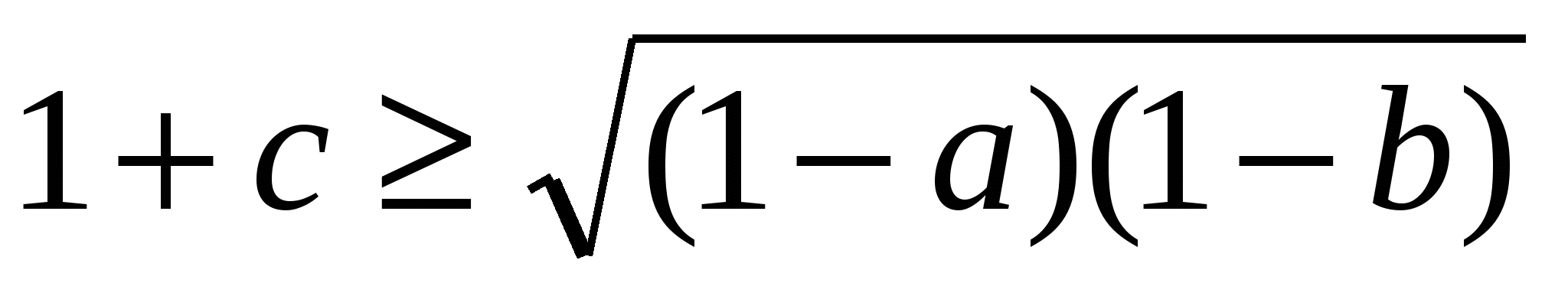 .Бұл теңсіздіктерді мүшелеп көбейтсек , дәлелденілетін теңсіздік шығады.
.Бұл теңсіздіктерді мүшелеп көбейтсек , дәлелденілетін теңсіздік шығады.
9-сынып
№1.Оң x,y,z сандары үшін теңсіздікті дәлелдеңдер:
x(1+y)+y(1+z)+z(1+x)≥6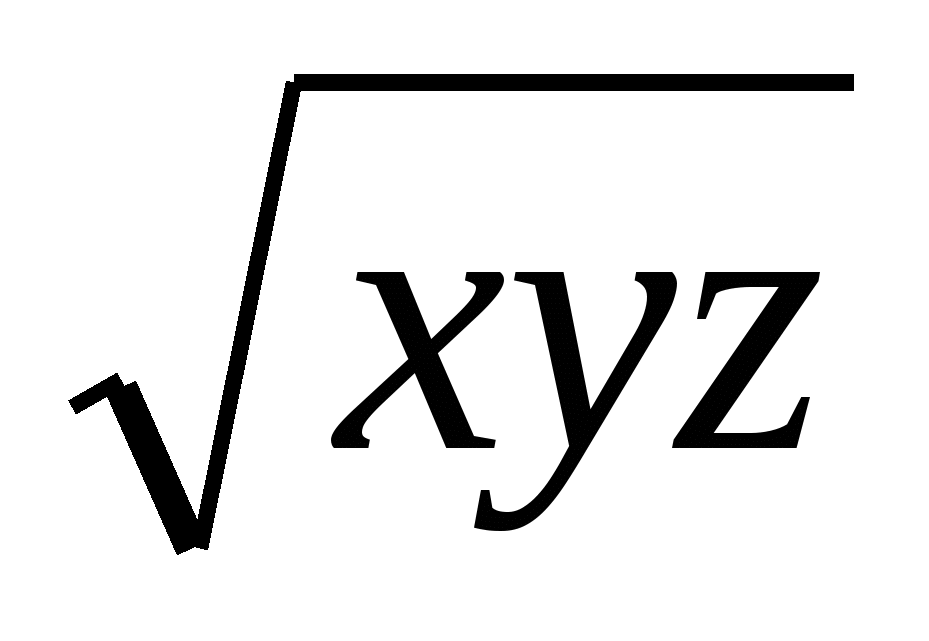
Дәлелдеуі:Белгілі а+в≥2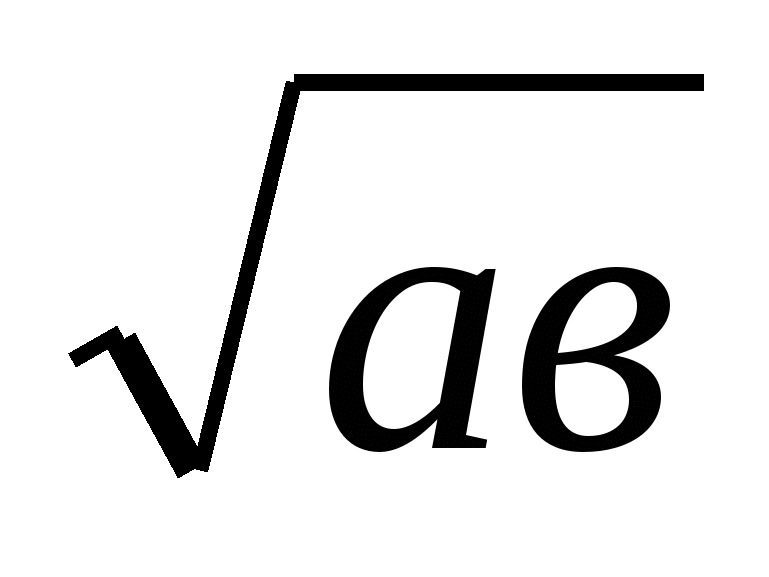 теңсіздігін (а,в, ≥0) пайдаланып x+yz≥2
теңсіздігін (а,в, ≥0) пайдаланып x+yz≥2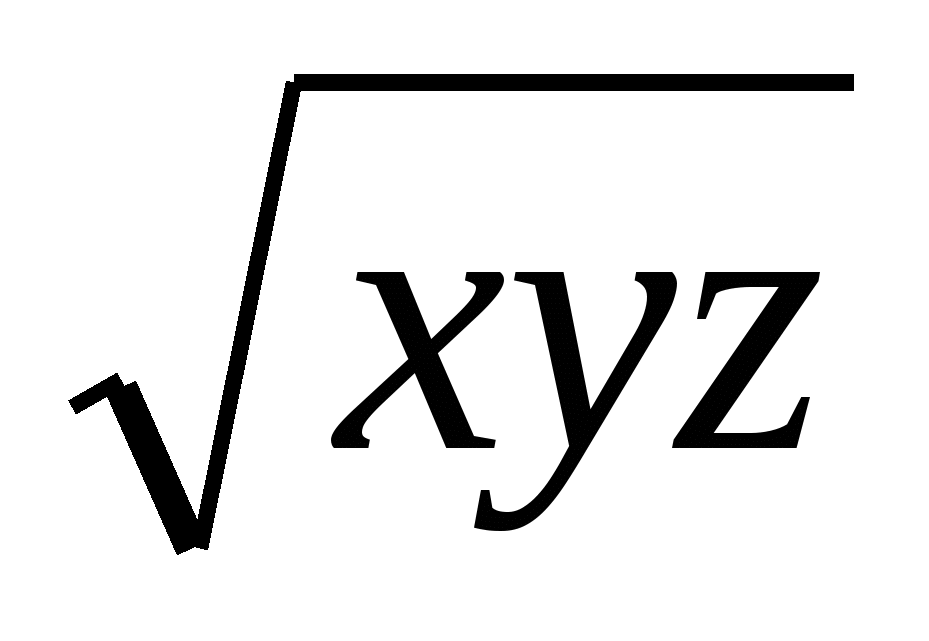 , y+xz≥2
, y+xz≥2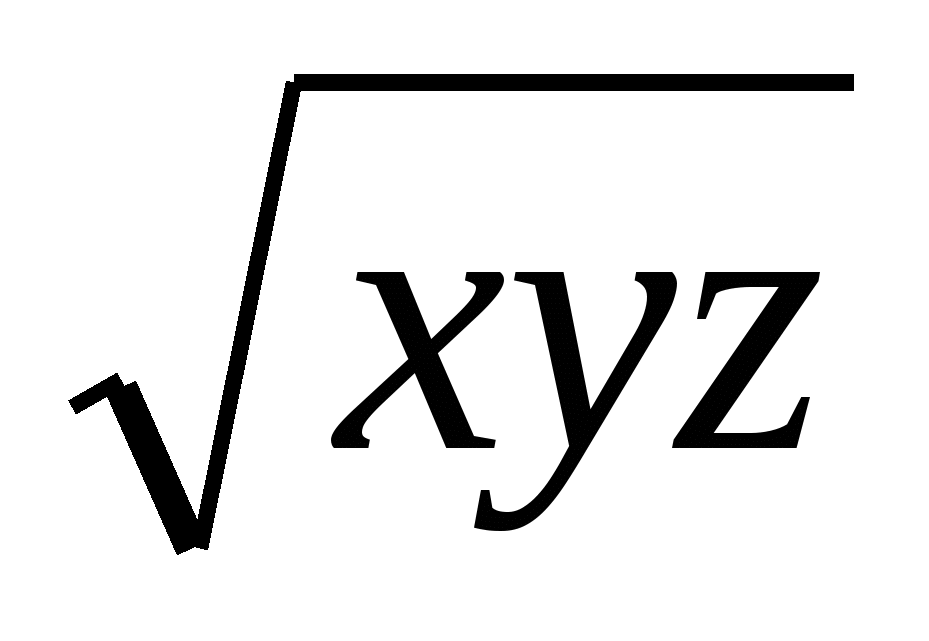 , z+xy≥2
, z+xy≥2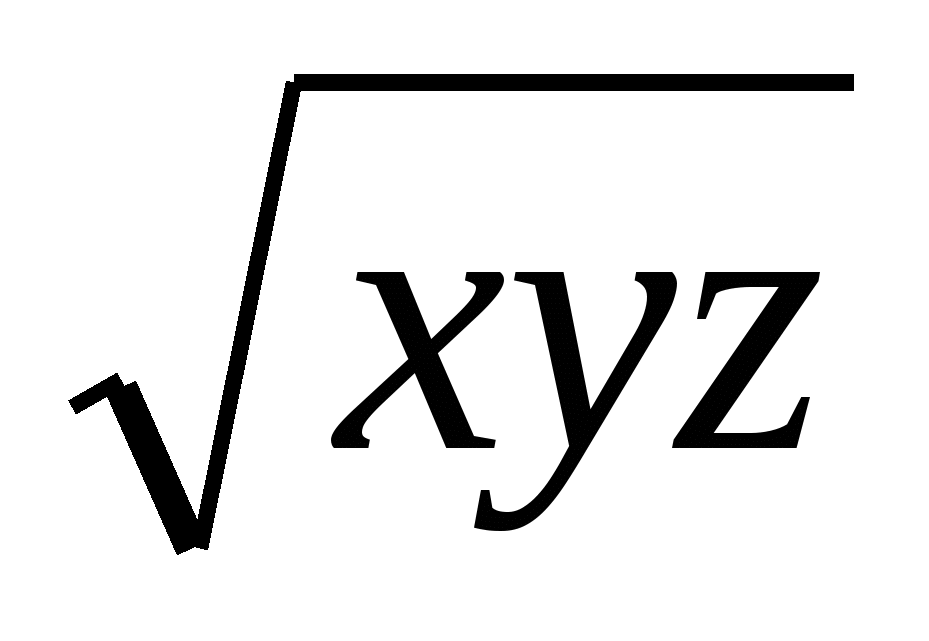 теңсіздіктерін аламыз. Осы үш теңсіздікті қосып
теңсіздіктерін аламыз. Осы үш теңсіздікті қосып
x+yz+y+xz+z+xy=x(1+y)+y(1+z)+z(1+x)>6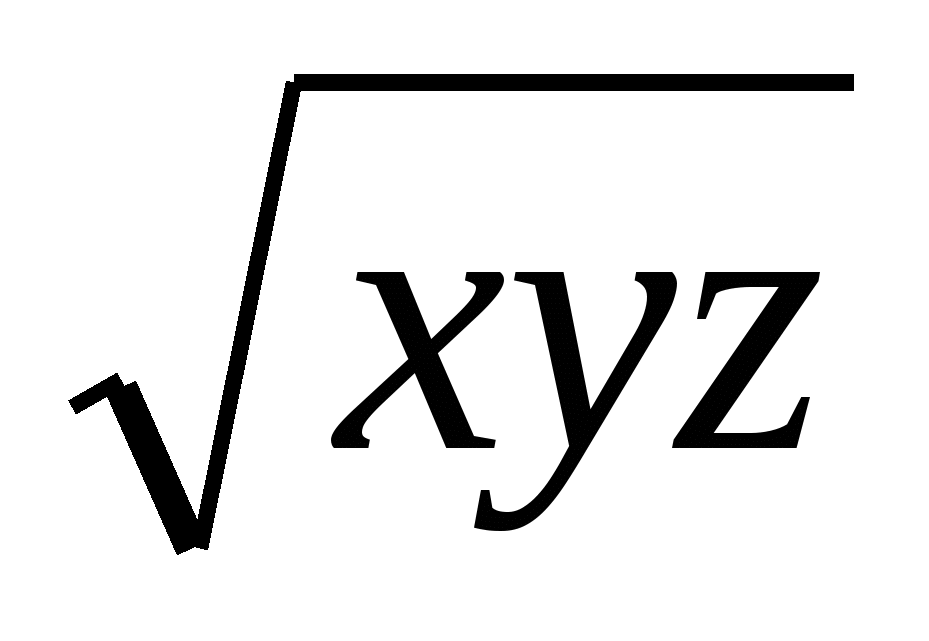 теңсіздігін аламыз.
теңсіздігін аламыз.
10-сынып.
№1.Теріс емес а,в үшін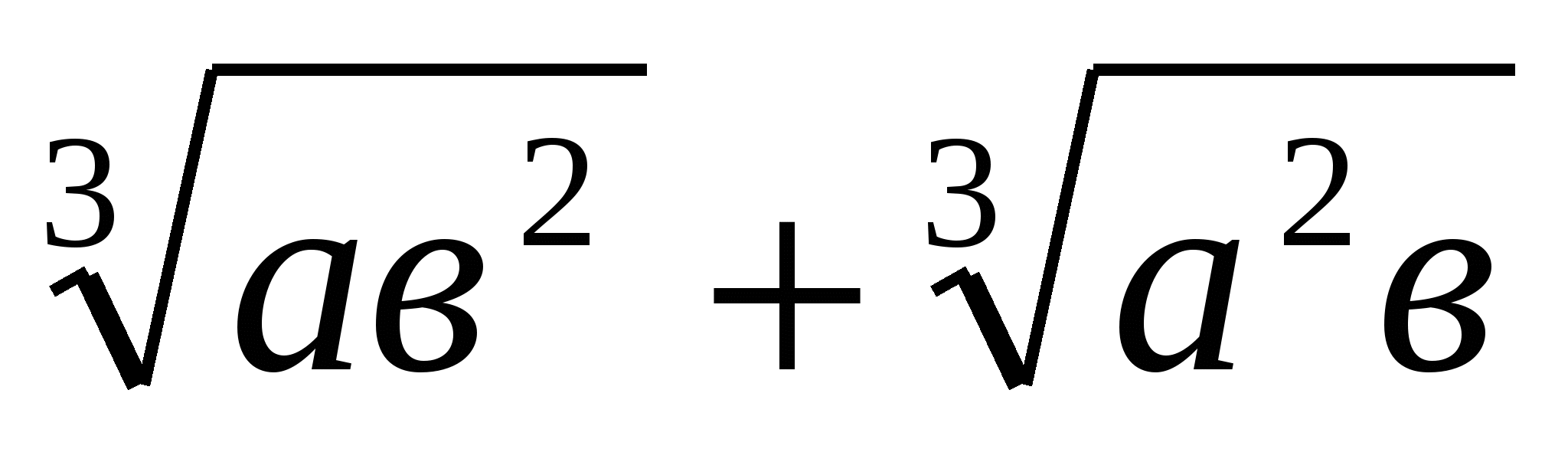 ≤а+в теңсіздігін дәлелдеңдер.
≤а+в теңсіздігін дәлелдеңдер.
Бізге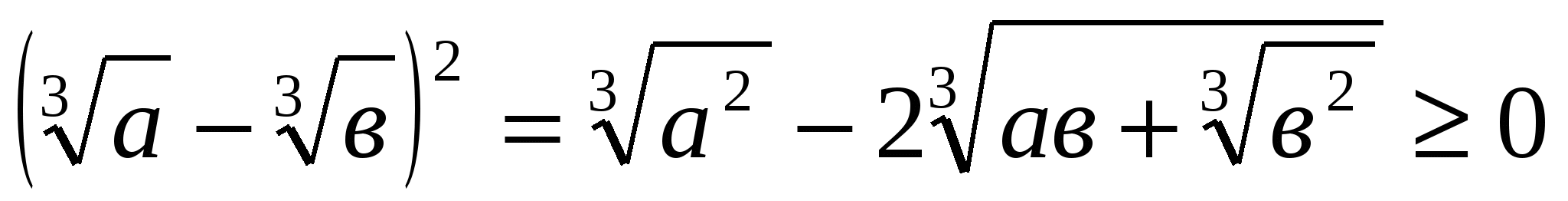 теңсіздігінен
теңсіздігінен 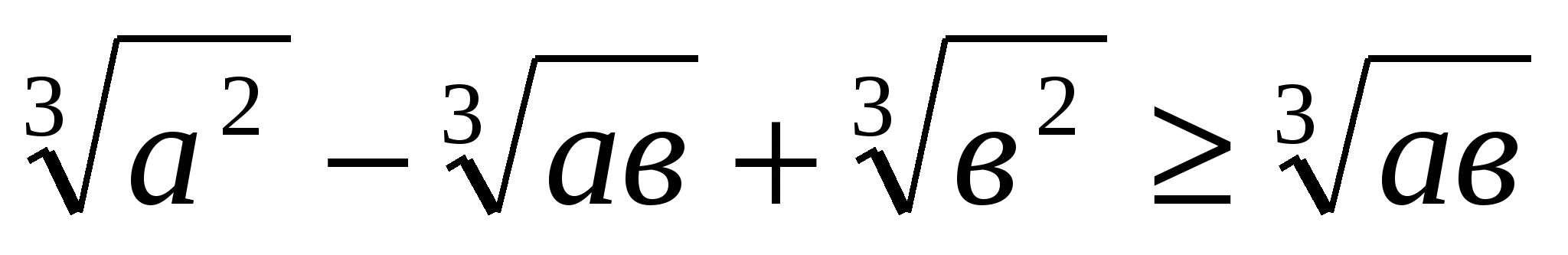
шығатыны анық.Соңғы теңсіздіктің екі жағын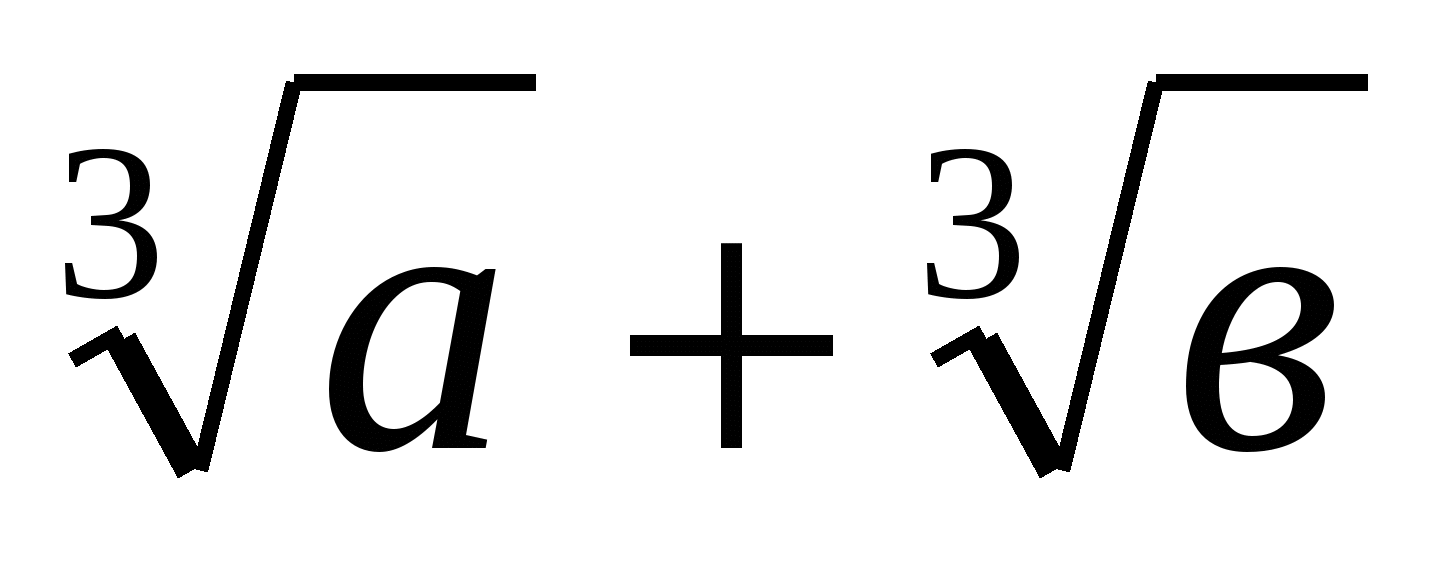 -қа көбейтсек, бізге керекті теңсіздік шыға келеді.
-қа көбейтсек, бізге керекті теңсіздік шыға келеді.
3.5 Халықаралық олимпиада
№1. а,в,с оң сандар болып және авс=1. Мынадай теңсіздікті дәлелдеңіздер:
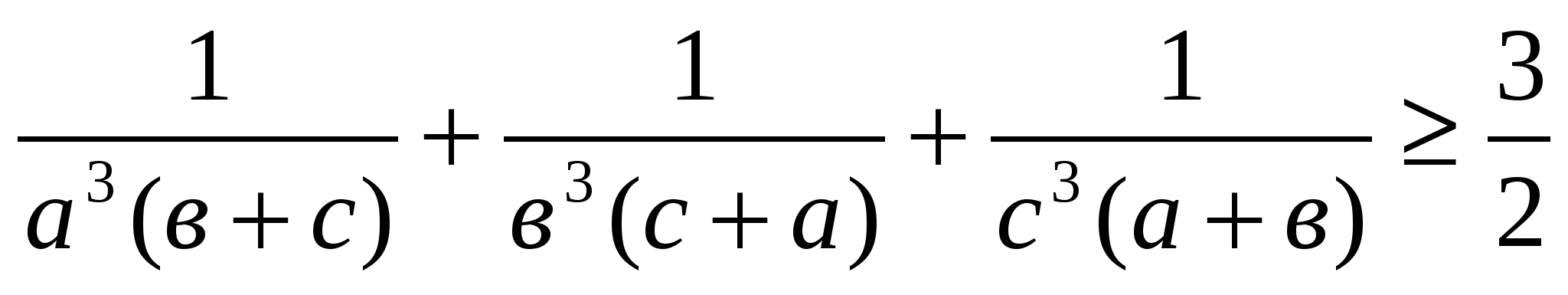
Дәлелдеуі:Жаңа белгілер енгізейік: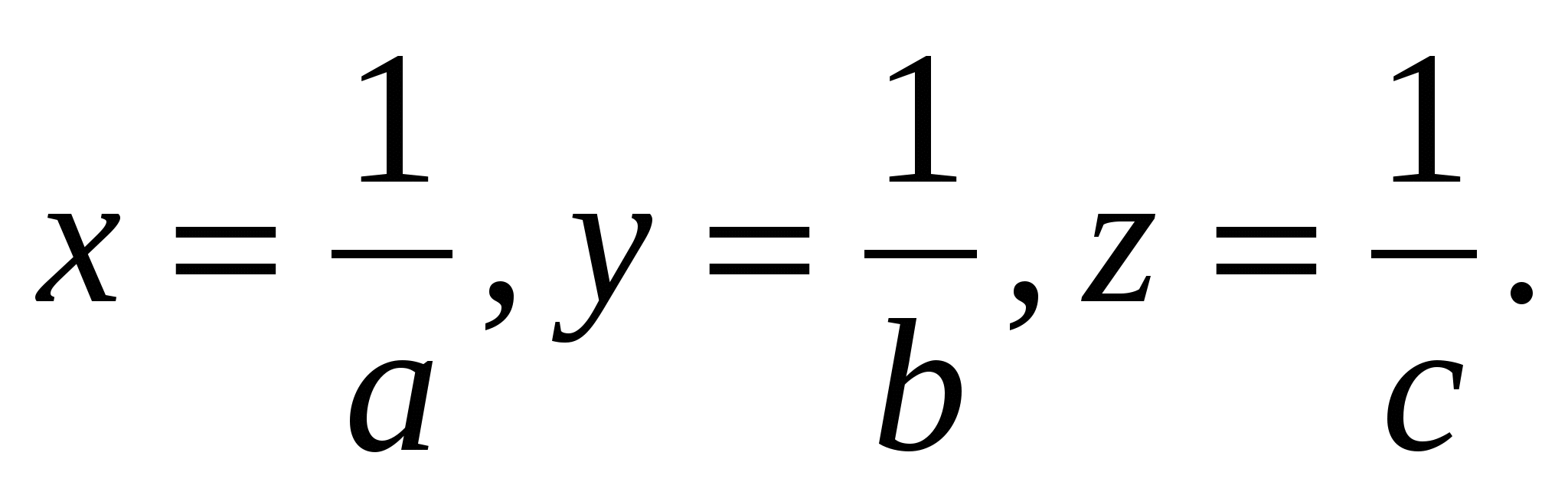
Есептің шарты бойынша xyz=1.Енді дәлелденілетін теңсіздік мынадай теңсіздікпен мәндес болады.
S=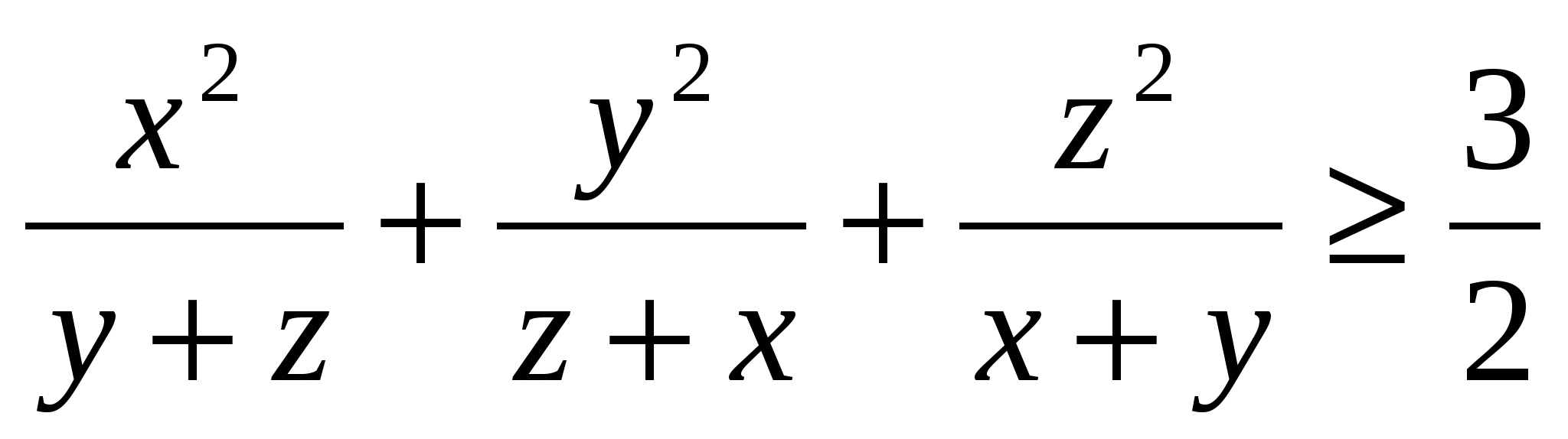
(1)
Біз оң сандардың арифметикалық ортасы мен геометриялық ортасының арасындағы байланысты қолданамыз: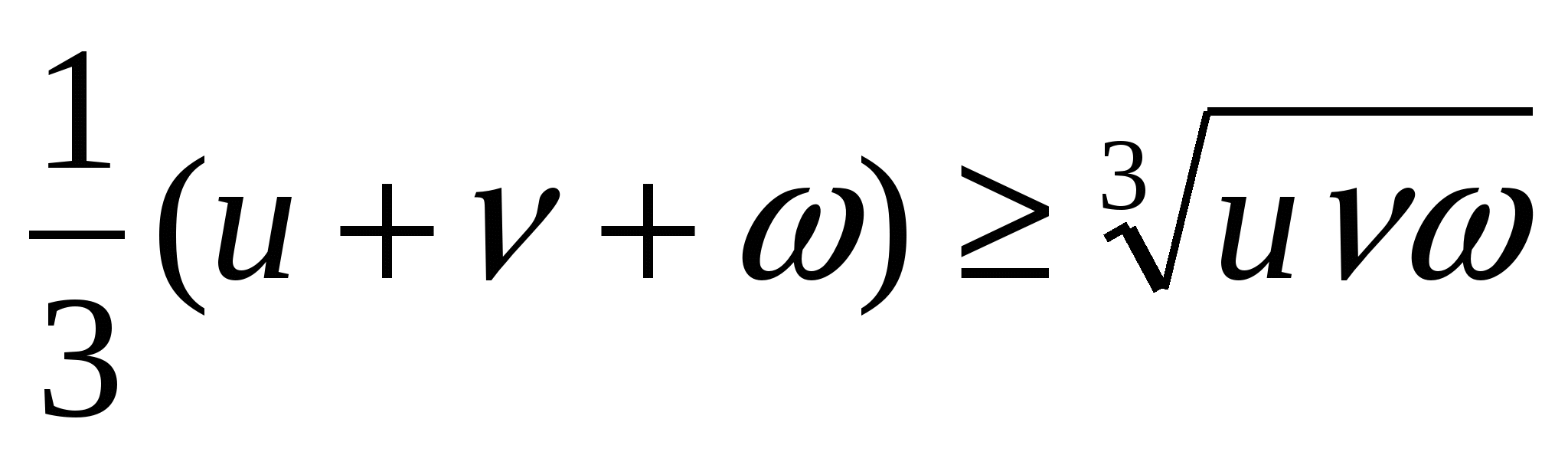 (2)
(2)
Енді Коши-Буняковский теңсіздігін қолданамыз:
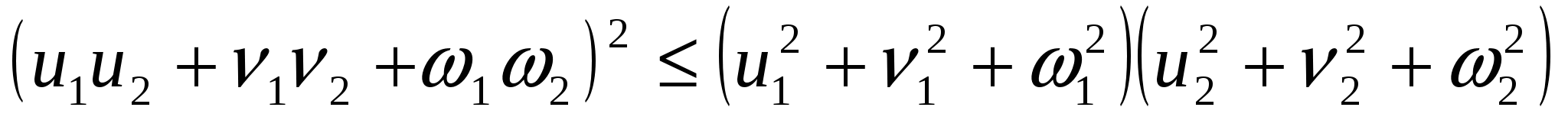
бұл теңсіздікті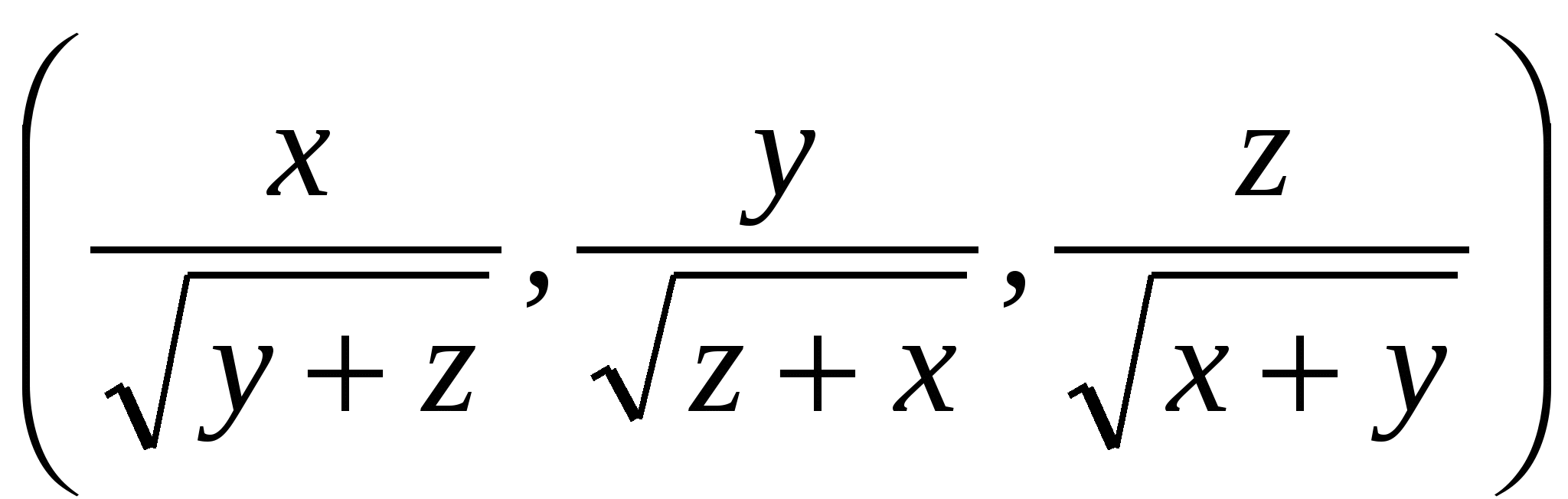 және
және 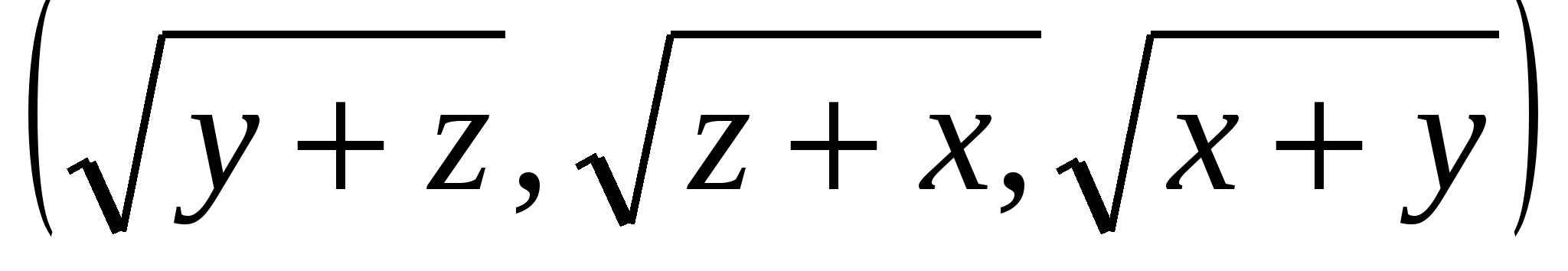 векторларына қолданып жазамыз:
векторларына қолданып жазамыз: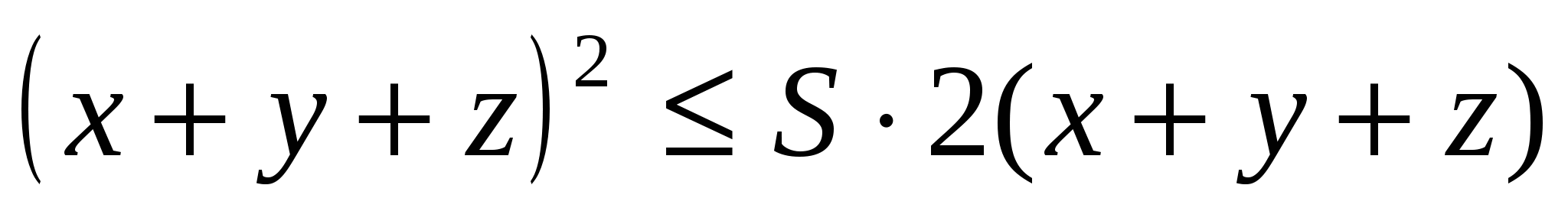 немесе
немесе 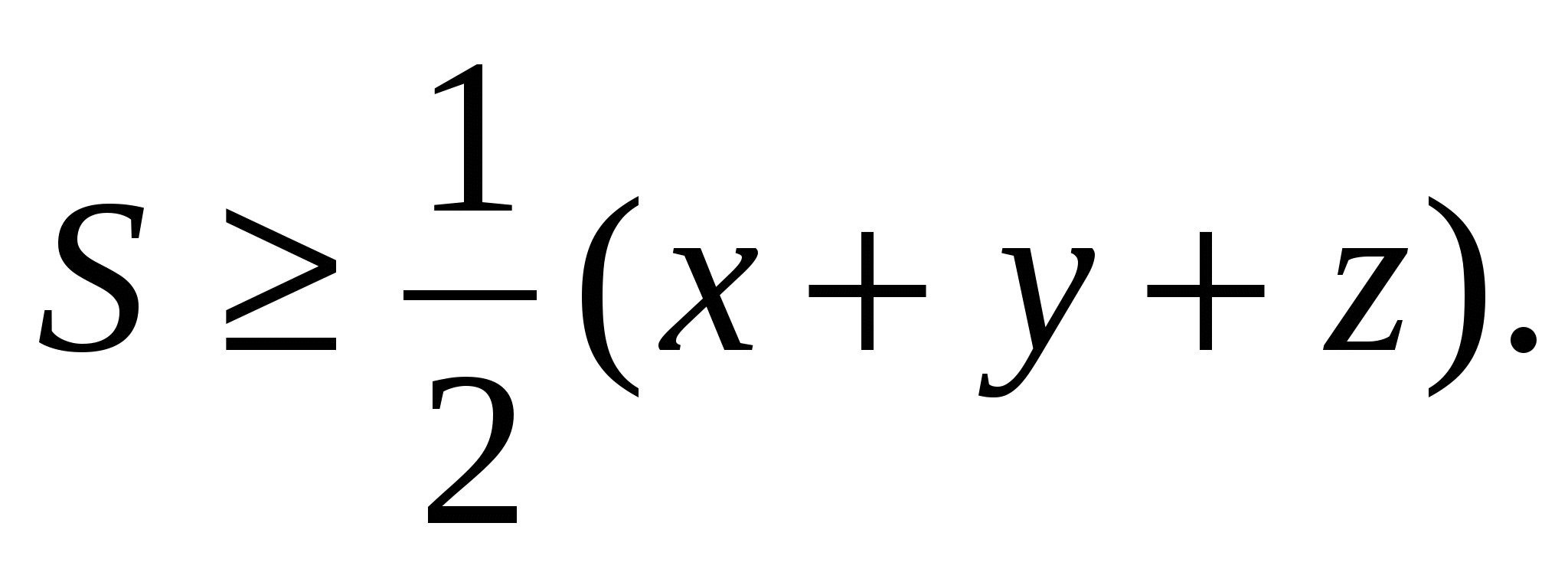
Енді 2) теңсіздікті қолданып табамыз
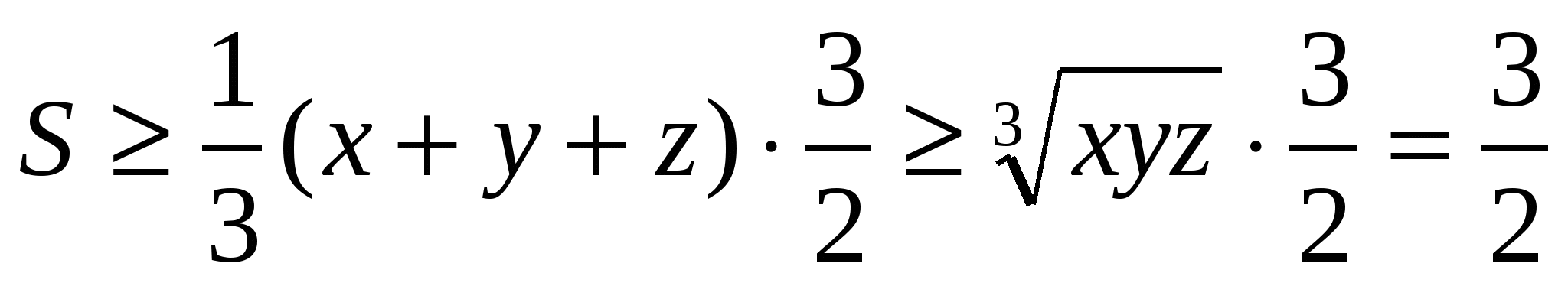
№2. Ауданы S келетін үшбұрыштың қабырғалары а,в,сболсын. Мынадай теңсіздікті дәлелдеңіздер: а2+в2+с2≥4S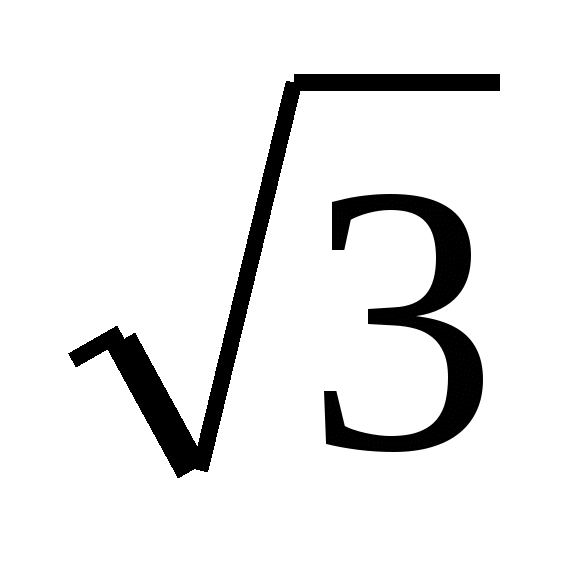 . Теңдік қашан болады?
. Теңдік қашан болады?
Дәлелдеуі: Герон формуласын жазайық.
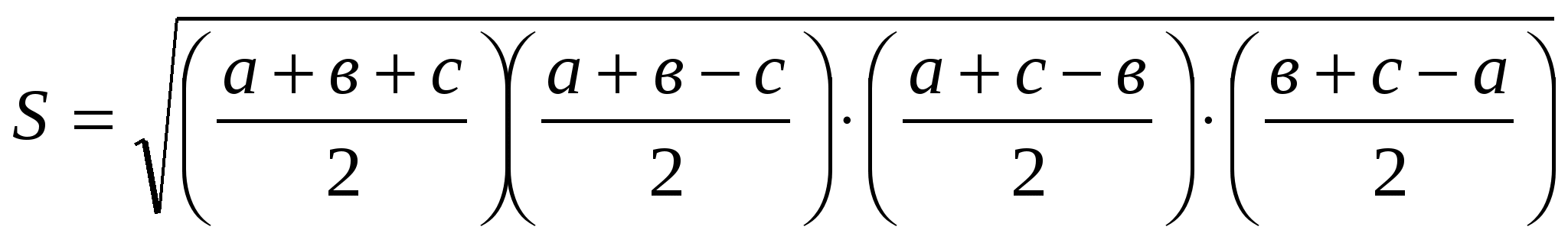
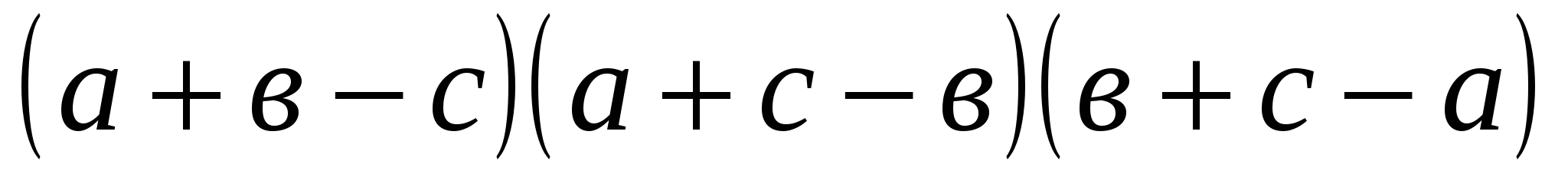 көбейтіндісын бағалау үшін мынадай теңсіздікті қолданайық
көбейтіндісын бағалау үшін мынадай теңсіздікті қолданайық 
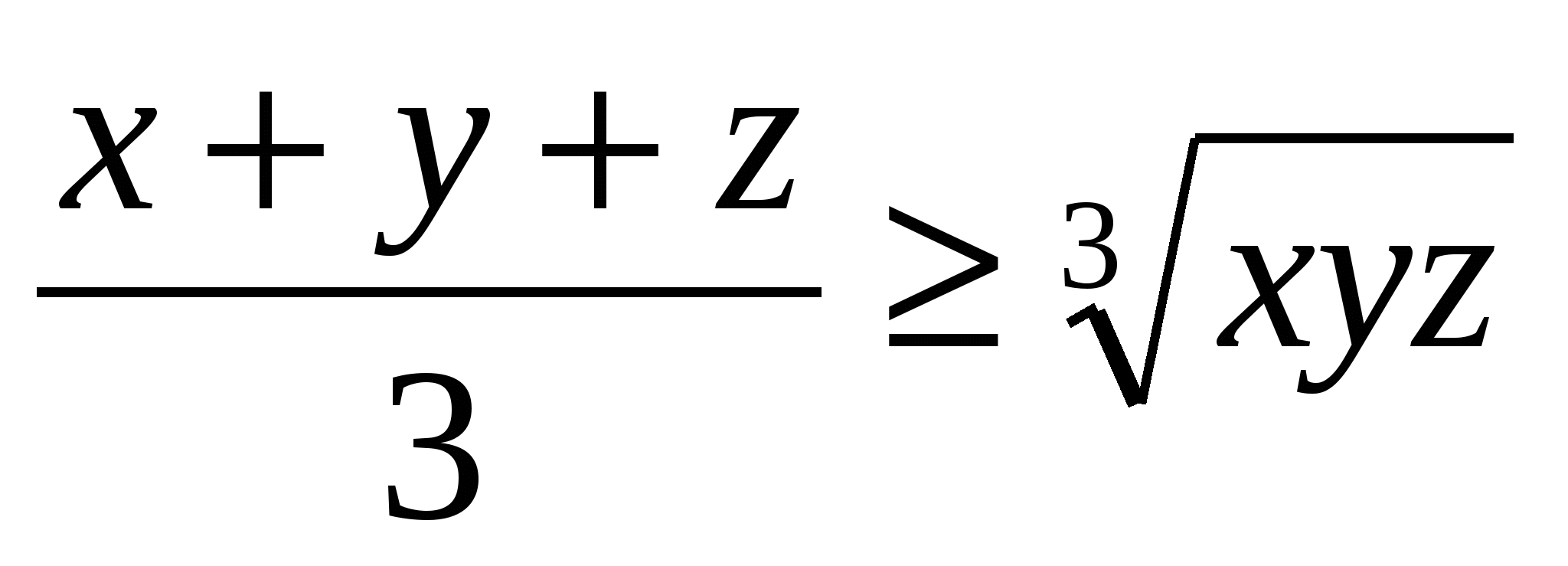 немесе xyz
немесе xyz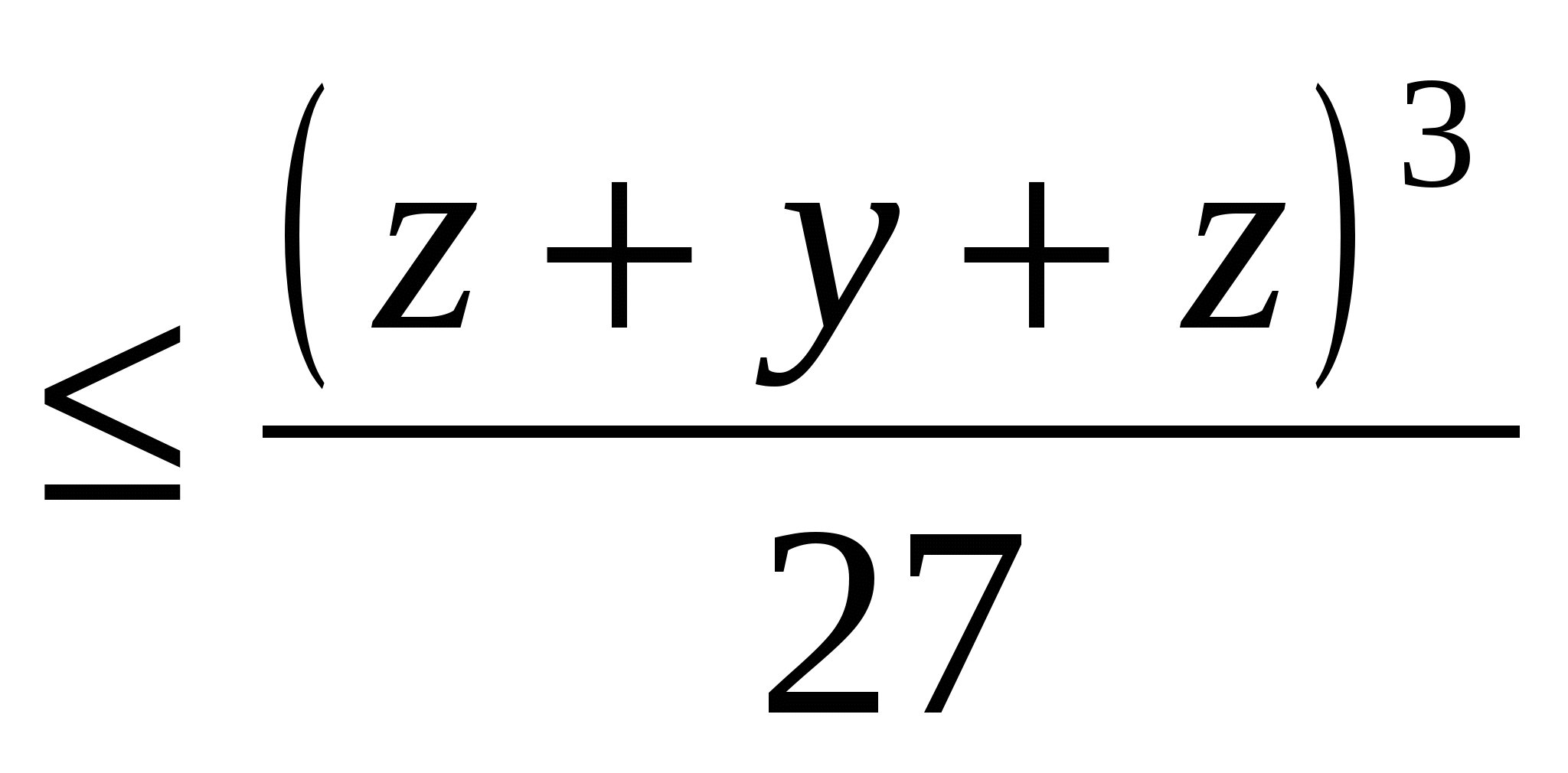 . Белгілеулер енгізейік:
. Белгілеулер енгізейік: 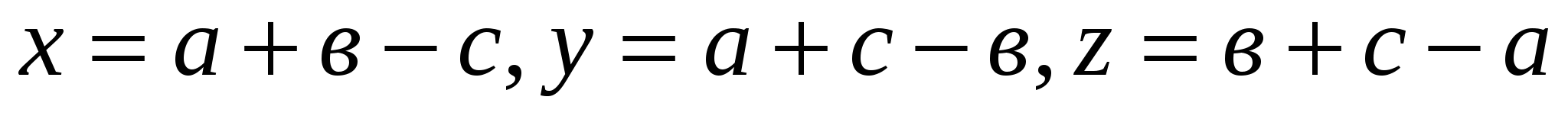 . Енді мынадай теңсіздіктерді жазуға б
. Енді мынадай теңсіздіктерді жазуға б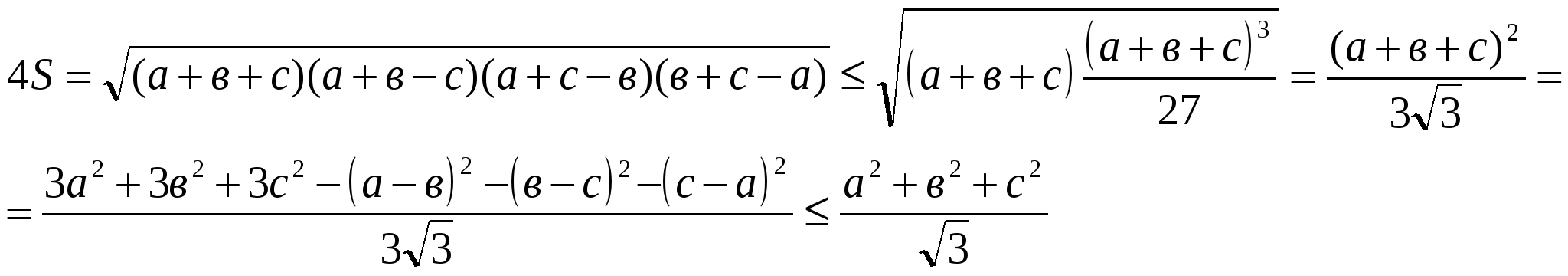 олады:
олады:
теңдік а=в=с болғанда орындалады.
Қорытындылай келе, қазіргі уақытта білім беру қызметкерлерінің алдында тұрған басты мақсат- еліміздегі білім беруді халықаралық деңгейге көтеру және білім сапасын көтеру, жеке тұлғаны қалыптастыру, қоғам қажеттілігін өтеу, оны әлемдік білім кеңістігіне кіріктіру болмақ. Сондықтан, математика пәнінен деңгейі жоғары оқушылармен олимпиадалық есептерді дайындық ретінде қарастыруға болады деп ойлаймын.
Қорытынды
Оқушыларды жеке тұлға етіп тәрбиелеудегі математика пәні мұғалімінің жоғары оқу орнында білім алып жатқан кездерінентақырыпты оқытудың әдістерін зерттеп, талдатудың болашақтағы қызметтері үшін алатын орны, салмағы зор. Сондықтан,мақала алгебра курсында қарастырылатын «Теңсіздіктерді дәлелдеу» тақырыбын оқытудың әдістеріне студенттердің болашақ маман ретінде жүргізген зерттеу жұмыстарына негізделініп отыр.
Сонымен қоса, студенттердің «Теңсіздіктерді дәлелдеудің» барлық әдісінқарастырып, оны тақырыпты меңгертуде қолданудың жолдарын өздігінше пайымдауы, аудиторияда шешім шығарушы оқытушы ғана емес, студент те болатындығы туралы оларда оң пікір қалыптастырады.
Педагогикалық мәселелер мен оларды зерттеу мақсаты ғылыми жаңалық талаптарын қанағаттандыратын, белгілі бір нәтижелер қайталанбай, әдістемені жетілдіру бағытында болуы керек екендігін ескерсек, жоғары оқу орындарында оқытудың аталғандай ұйымдастырылуы нәтижелі деген қорытындыға келеміз.
Кең түрде қолданылатын классикалық Коши теңсіздігін, «Математикалық индукция», «Анализ», «Реттелген жиындар» тәсілдерімен шеше отырып, олардың бір-бірінен ерекшелігі ашып көрсетілді. Теңсіздіктер математикада ғана емес, экологиялық, экономикалық, халық шаруашылығындағы байланыстарда ерекше роль атқарады. Теңсіздіктердің осындай маңыздылығын ескере отырып, мектеп математикасына санды, алгебралық теңсіздіктермен бірге классикалық теңсіздіктер теориясын тереңірек еңгізіп қарастырса артық болмас деп ойлаймын.
Пайдаланылған әдебиеттер
9-сынып
№1. a>в>0 сандары үшін
Дәлелдеуі: Дәлелденетін теңсіздік мынадай теңсіздікпен мәндес:
немесе
немесе
немесе
немесе
Соңғы теңсіздік тура болғандықтан дәлелденілетін теңсіздік те тура болады.
3.4 Республикалық олимпиада
11-сынып
№1.а+в+с=1, (a,в,с≥0) шарттарын қанағаттандыратын а,в,с сандары үшін теңсіздікті дәлелдеңіздер. (1+а)(1+в)(1+с)≥8(1-а)(1-в)(1-с).
Дәлелдеуі: 1+а=(1-в)+(1-с) онда 1+
9-сынып
№1.Оң x,y,z сандары үшін теңсіздікті дәлелдеңдер:
x(1+y)+y(1+z)+z(1+x)≥6
Дәлелдеуі:Белгілі а+в≥2
x+yz+y+xz+z+xy=x(1+y)+y(1+z)+z(1+x)>6
10-сынып.
№1.Теріс емес а,в үшін
Бізге
шығатыны анық.Соңғы теңсіздіктің екі жағын
3.5 Халықаралық олимпиада
№1. а,в,с оң сандар болып және авс=1. Мынадай теңсіздікті дәлелдеңіздер:
Дәлелдеуі:Жаңа белгілер енгізейік:
Есептің шарты бойынша xyz=1.Енді дәлелденілетін теңсіздік мынадай теңсіздікпен мәндес болады.
S=
(1)
Біз оң сандардың арифметикалық ортасы мен геометриялық ортасының арасындағы байланысты қолданамыз:
Енді Коши-Буняковский теңсіздігін қолданамыз:
бұл теңсіздікті
Енді 2) теңсіздікті қолданып табамыз
№2. Ауданы S келетін үшбұрыштың қабырғалары а,в,сболсын. Мынадай теңсіздікті дәлелдеңіздер: а2+в2+с2≥4S
Дәлелдеуі: Герон формуласын жазайық.
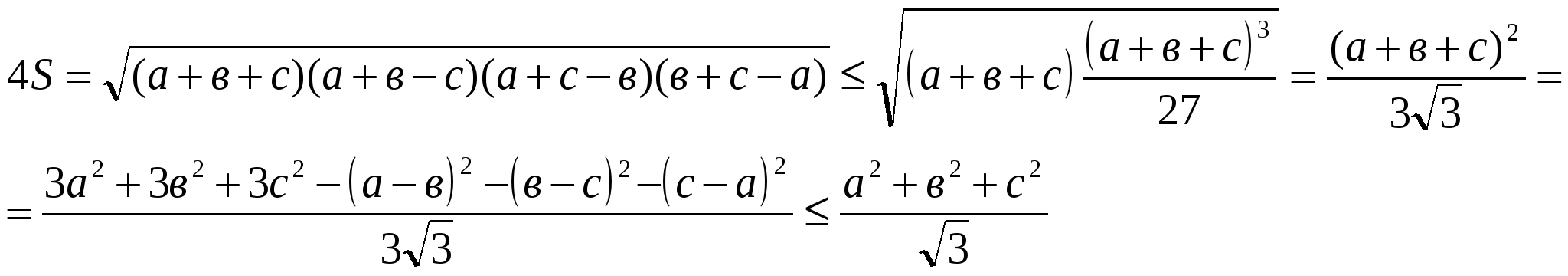 олады:
олады:теңдік а=в=с болғанда орындалады.
Қорытындылай келе, қазіргі уақытта білім беру қызметкерлерінің алдында тұрған басты мақсат- еліміздегі білім беруді халықаралық деңгейге көтеру және білім сапасын көтеру, жеке тұлғаны қалыптастыру, қоғам қажеттілігін өтеу, оны әлемдік білім кеңістігіне кіріктіру болмақ. Сондықтан, математика пәнінен деңгейі жоғары оқушылармен олимпиадалық есептерді дайындық ретінде қарастыруға болады деп ойлаймын.
Қорытынды
Оқушыларды жеке тұлға етіп тәрбиелеудегі математика пәні мұғалімінің жоғары оқу орнында білім алып жатқан кездерінентақырыпты оқытудың әдістерін зерттеп, талдатудың болашақтағы қызметтері үшін алатын орны, салмағы зор. Сондықтан,мақала алгебра курсында қарастырылатын «Теңсіздіктерді дәлелдеу» тақырыбын оқытудың әдістеріне студенттердің болашақ маман ретінде жүргізген зерттеу жұмыстарына негізделініп отыр.
Сонымен қоса, студенттердің «Теңсіздіктерді дәлелдеудің» барлық әдісінқарастырып, оны тақырыпты меңгертуде қолданудың жолдарын өздігінше пайымдауы, аудиторияда шешім шығарушы оқытушы ғана емес, студент те болатындығы туралы оларда оң пікір қалыптастырады.
Педагогикалық мәселелер мен оларды зерттеу мақсаты ғылыми жаңалық талаптарын қанағаттандыратын, белгілі бір нәтижелер қайталанбай, әдістемені жетілдіру бағытында болуы керек екендігін ескерсек, жоғары оқу орындарында оқытудың аталғандай ұйымдастырылуы нәтижелі деген қорытындыға келеміз.
Кең түрде қолданылатын классикалық Коши теңсіздігін, «Математикалық индукция», «Анализ», «Реттелген жиындар» тәсілдерімен шеше отырып, олардың бір-бірінен ерекшелігі ашып көрсетілді. Теңсіздіктер математикада ғана емес, экологиялық, экономикалық, халық шаруашылығындағы байланыстарда ерекше роль атқарады. Теңсіздіктердің осындай маңыздылығын ескере отырып, мектеп математикасына санды, алгебралық теңсіздіктермен бірге классикалық теңсіздіктер теориясын тереңірек еңгізіп қарастырса артық болмас деп ойлаймын.
Пайдаланылған әдебиеттер
-
«Математика в школе» №3; 1991 -
Алгебра оқулығы 9-кл. А.Е. Әбілқасымова, Н.Р.Майкотов , Қ.И.Қаңлыбаев. -
Алгорифм 2004 жыл №3 -
Б.А.Қадырбаева. Студенттерді «Рационал көрсеткішті дәрежелер» тақырыбын интербелсенді әдіспен оқытуға даярлау, Шоқан тағылымы Халық/қ ғыл-пр конф. Көкшетау, 2009 -
Глейзер Г.И. «История математики в школе». М – 1983 ж -
Жәуітіков О.А. «Жоғары математикаға кіріспе» Мектеп 1984 ж -
И.Н. Бронштейн «Справочник по математике», М – 1964 ж -
Математика в школе 1979 жыл №4 -
Математика в школе 1981 жыл №3 -
Математика,физика №2; 2003 -
Т.Т.Абылайханов , Т.Т. Абылайханов «Математика есептері»