Файл: 1. Алгебрада тесіздіктерді длелдеу дістері.doc

Скачать файл (2,47Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 119

Скачиваний: 8

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

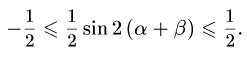
Симметриялық және біртекті қасиеттерді қолдану

№7 Теңсіздікті дәлелде:

Дәлелдеуі:

Теңсіздікті түрлендіре отырып келесі түрге көшеміз

x, y, z айнымалы арқылы симметриялық теңсіздік аламыз, бұдан x

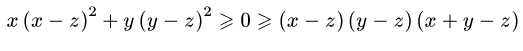
2.5 Математикалық индукция тәсілін қолдану

Теңсіздіктерді дәлелдеуде математикалық индукция тәсілін қолдануға болады. Математикалық индукция принциптерін келесі берілген тұжырымдамада барлық натурал n сандары p-дан кіші емес үшін ақиқат, егер:

1) n=p үшін тұжырымдама ақиқат болса,

2) n=k(k

p) тұжырымдама ақиқат деп, n=k+1 үшін тұжырымдама ақиқат екенін дәлелдеу керек.

№8. Дәлелдеу керек:

мұндағы n>1, n

N

Дәлелдеуі:

n=2 ,

ақиқат

n=k тұжырымдама ақиқат деп алып

n=k+1 тұжырымдаманың ақиқат екенін дәлелдейміз

n(n>1)

Бір теңсіздікті бірнеше рет қолдану тәсілі

№9. Қос теңсіздікті дәлелдеу керек:

,

a>0, b>0, c>0, d>0.

Дәлелдеуі:

x>0, y>0

осы теңсіздікті бірнеше рет қолданып дәлелдейміз

2.6 Туынды мен интегралды қолданып дәлелдеу тәсілі

Егер функция f(x) және g(x) І аралығында анықталса, және үздіксіз болса, онда, f(x)

g(x) теңсіздігін [a,b]=I немесе [a, +∞)=I аралығында дәлелдеу үшін, келесі теореманы қолдануға болады:

Теорема: Егер f(x) және g(x) І аралығында дифференциалданса,

f(a)

g(a) осы аралықта және h’(x)

0, мұндағы h(x)= f(x) – g(x), онда

f(x)

g(x) теңсіздігі осы аралықта орындалады.

№1. 2x+1>x+2, x

1 теңсіздікті дәлелде.

Дәлелдеуі: функция h(x)=2x+1-x-2 [1,+∞) аралығындағы функцияны қарастырамыз.

h(1)=1 және h/(x)=2x+1ln2-1 функциясы y=2x [1, +

) аралығында өспелі болады, ендеше h/(x)

4ln2-1>0 бұдан x

1, h(x)

h(1) болса немесе

2x+1

x+3,

2x+1>x+2 онда орындалады.

3.Олимпиадада теңсіздіктерді шешу және дәлелдеу

әдістері

3.1 Мектепішілік олимпиада

№1.Теңсіздікті дәлелдеңдер.

(a+в+c)(

)≥9 (мұндағы а>0, в>0,с>0)

Теңсіздіктің сол бөлігін түрлендірейік:

_(a+в+c)(

)=1+

+1+

+1=3(

)+(

)≥

≥3+2+2+2=9 (себебі әр жақшаның ішіндегі қосынды 2-ге тең немесе одан үлкен).

№2.

≥а1 а2 а3 а4 (мұндағы а1 >0,а2>0, а3>0, а4 >0 )

Нұсқау.Екі оң санның арифметикалық орташасы мен геометриялық орташасын екі рет салыстыруды қолданамыз.

№3.Егер а2+в2 =1 болса , │а+в│≤

онда екенін дәлелдеңіздер.

және

екені есептің шартынан шығады. Сондай –ақ а2+в2 =1 болғандықтан, а мен в-ны синуспен және косинуспен ауыстыруға болады: a=sinα , в=cosα. Ондаа+в=sinα+cosα=sinα+sin

= =2sin

cos

.

cos

≤1.Демек , │а+в│≤

.

Басқаша талқылап көрелік: 1=а2+в2≥2

; 2≥а2+в2+2

;

≥

3.2 Аудандық олимпиада

11-сынып

№1.Теңсіздікті шеш:

>0

Теңсіздіктің сол жағын ортақ бөлімге келтіріп ықшамдап жазайық.

>0

онда берілген теңсіздікке мәндес теңсіздік

>0 болады.

-7

-5 0 5

.
№2.Теріс емес, а,в,с сандары үшін теңсіздікті дәлелдеңдер:(а+в)(в+с)(с+а)≤8

Нұсқау:Мынадай үш теңсіздікті көбейту керек

.

10-сынып.

№1.х-кез-келген сан болсын, дәлелдеңдер:

Дәлелдеуі: x(x+3)(x+1)(x+2)=(x2+3x)(x2+3x+2)=((x2+3x+1)-1)((x2+3x+1)+1)=(x2+3x+1)2-1≥-1

3.3 Облыстық олимпиада

10-сынып

№1.Теңсіздікті дәлелдеңдер.