Файл: Контрольные вопросы для самопроверки знаний по разделу дисциплины физической химии Химическая термодинамика.doc

Решение.

1) Представим процесс нагревания вещества от Т₁ и Т₂по стадиям:

1 стадия. Твердое вещество (при Т₁)

нагревание



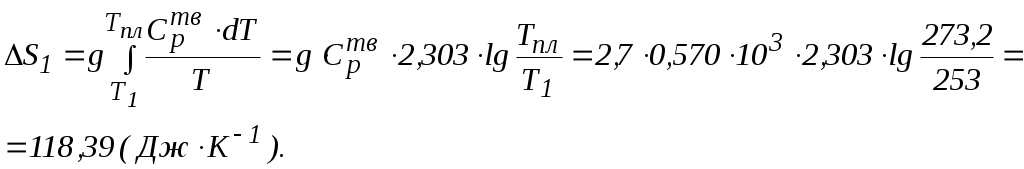
2 стадия. Твердое вещество (при Т_пл.)

.

3 стадия. Жидкость (при Т_пл.)

нагревание



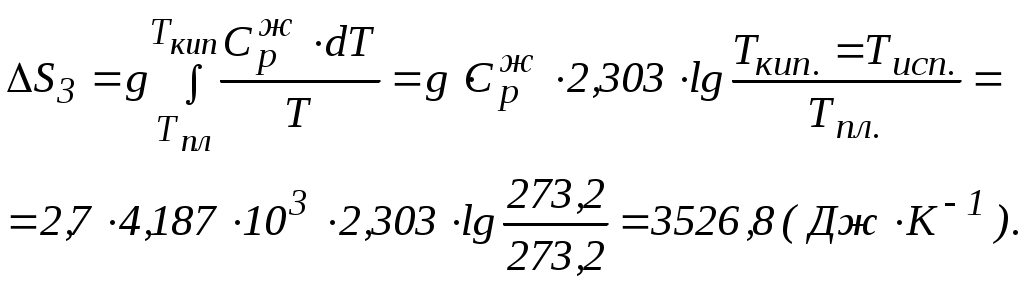
4 стадия. Жидкость (при Т_кип.)

кипение



5 стадия. Пар (при Т_кип.) Пар (при Т₂)

нагревание



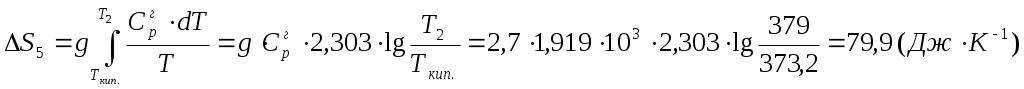
Находим изменение энтропии при нагревании вещества от Т ₁ до Т_2.
.
Изменение стандартной энтропии системы при протекании химической реакции определяется как разность суммы стандартных энтропий продуктов и суммы стандартных энтропий исходных веществ.
(4.25)

Значения величин стандартных энтропий (определенных для стандартных условий) веществ приведены в справочниках.

Энтропия, как критерий возможности протекания процесса в изолированной системе (U,V = const). Изолированная система не обменивается с окружающей средой теплотой, т.е. . Поэтому, согласно второго закона термодинамики

(dS)

---

_U,V ≥ 0. (4.26)

Необратимый процесс в изолированной системе возможен при

(dS)_U,V > 0. (4.27)

При равновесном состоянии системы (или обратимом процессе)

(dS)_U,V = 0; (4.28)

при этом энтропия принимает максимальное значение S = S_max.

Если (dS)_U,V < 0 (4.29)

– необратимый процесс в изолированной системе неосуществим.


Л е к ц и я 5
ТЕРМОДИНАМИКА АГРЕГАТНЫХ ПРЕВРАЩЕНИЙ
План лекции: Уравнение Клайперона – Клаузиуса. Применение уравнения Клайперона – Клаузиуса к процессам испарения и возгонки. Зависимость давления насыщенного пара от температуры.
Фазовые переходы чистого вещества в двухфазной однокомпонентной системе представим следующим образом.

Фазовый переход:		Процесс:	При фазовом переходе:
α→β
Жидкость	Пар	И спарение	значительно изменяется объем;
Твердое	Пар	Возгонка
Твердое	Жидкость	П лавление	объем практически не изменяется;
Твердое	Твердое	Полиморфное превращение	(конденсированное состояние).

При равновесии или .

При этом

(5.1)

---

(5.2)

где - это мольные объемы вещества в фазах α и β,

- это энтропии вещества в фазах α и β.

Так как , получаем

Объединяем объемы и энтропии:

(5.3)

Отсюда (5.4)

где - это изменение энтропии при фазовом переходе;

- это изменение объема при фазовом переходе.

Так как получаем

, (5.5)

где - изменение давления насыщенного пара с температурой.

Уравнение (5.5) - это уравнение Клаузиуса-Клайперона,

Применение уравнения Клаузиуса-Клайперона к процессам испарения и возгонки.

«Жидкость пар» или «твердое пар».

или .

или .

Объемом конденсированного состояния (жидкости, твердого) можно пренебречь по сравнению с объемом пара и считать: .

Предложим, что пар подчиняется законам идеального газа, тогда Подставляем это выражение в уравнение (5.5):

---

, получаем: Так как , получаем

. (5.6)

Это уравнение Клаузиуса-Клайперона для процессов испарения и выгонки. Физический смысл уравнения: с ростом температуры давление насыщенного пара в системе растет.

При можно из уравнения Клаузиуса-Клайперона найти значение величины теплового эффекта и равновесного давления насыщенного пара. Преобразуем уравнение (5.6), получаем

(5.7)

Берем неопределенный интеграл выражения (5.7), после интегрирования:

(5.8)

Уравнение (5.8) отвечает уравнению прямой линии. Построим графическую зависимость , рис. 2. Из графика находим тангенс угла наклона α: , тогда .




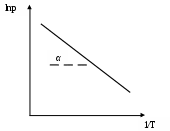
Рис. 2. Графическая зависимость



Возьмем определенный интеграл выражения (5.7), получаем:

. (5.9)

Л е к ц и я 6
ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
План лекции: Термодинамический потенциал. Изохорно-изотермический потенциал или свободная энергия Гельмгольца. Применение энергии Гельмгольца в качестве критерия направления самопроизвольного процесса и равновесия в закрытых системах. Изобарно-изотермический потенциал или свободная энергия Гиббса. Применение энергии Гиббса в качестве критерия направления самопроизвольного процесса и равновесия в закрытых системах. Характеристические функции: внутренняя энергия, энтальпия, свободная энергия Гельмгольца, свободная энергия Гиббса. Уравнения Гиббса-Гельмгольца. Химический потенциал.
Термодинамический потенциал – это функция состояния системы, убыль которой в процессе, протекающем при постоянстве двух параметров, равна максимальной полезной работе.

Энергия Гельмгольца как изохорно-изотермический потенциал.

Для изохорно-изотермических условий V = const, T = const. Вспомним, что объединенное уравнение, выражающее первый и второй законы термодинамики, имеет следующий вид: .

Так как при V = const, = 0, получим

. (6.1)

Проинтегрируем данное уравнение:

.

Введем обозначение F – это энергия Гельмгольца.

F = U - TS (6.2)

Тогда F₂ = U₂ - TS₂и F₁ = U₁ - TS₁.

, или

То есть энергия Гельмгольца – это термодинамический потенциал, так как его изменение равно полезной работе при протекании обратимого процесса в системе. Для необратимого процесса: В общем случае для обратимого и необратимого процессов справедливо выражение
(6.3)

Энергия Гельмгольца равна , отсюда

U = F+TS. (6.4)

То есть F – это та часть внутренней энергии, которая может быть превращена в работу, поэтому она называется свободной энергией; произведение TS – это энергия, которая выделяется в виде тепла, поэтому она называется связанной энергией.

Энергия Гельмгольца как критерий возможности протекания процесса. Дифференцируя выражение получим dF = dU – TdS - SdT . Подставляя вместо произведения TdS его выражение из «объединенного» уравнения TdS ≥ dU+pdV получим

dF ≤ - SdT - pdV. (6.5)

Так как SdT = 0 иpdV= 0 (при Т = const и V= const), тогда для изохорно-изотермических условий

(dF)_v,T≤ 0. (6.6)

В закрытых (замкнутых) системах при изохорно-ихотермических условиях:

• 
  если dF < 0, то процесс протекает самопроизвольно;
  

• 
  если dF > 0, то процесс не протекает;
  

• 
  если dF = 0, то система находится в состоянии равновесия.
  

Энергия Гиббса как изобарно-изотермичесий потенциал. Для изобарно-изотермических условий р = const , T = const. Преобразуем объединенное уравнение первого и второго законов термодинамики:

как (6.7)

Проинтегрируем это выражение:

или

.
Введем обозначение

- это энергия Гиббса. (6.8)

Тогда

, ,

То есть энергия Гиббса G – это термодинамический потенциал, так как его изменение равно полезной работе при протекании обратимого процесса в системе. Для необратимого процесса В случае для обратимого и необратимого процесса справедливо выражение

(6.9)
Энергия Гиббса равна , но Поэтому отсюда . (6.10)

---

Энергия Гиббса G – эта часть энтальпии, которая может быть превращена в работу; поэтому она называется свободной энергией.

В выражение для энергии Гиббса подставим энергию Гельмгольца, которая определяется как F= U - TS. Тогда получим, что или . (6.11)
Энергия Гиббса, как критерии возможности протекания процесса.

Продифференцируем выражение , получим



Вместо TdS подставим его значение из объединенного уравнения первого и второго законов термодинамики Тогда

или

(6.12)

В изобарно-изотермических условиях и

. (6.13)

То есть dG является критерием возможности протекания процесса в замкнутой (закрытой) системе в изобарно-изотермических условиях. При этом

• 
  если dG < 0, то процесс протекает самопроизвольно;
  
• 
  если dG > 0, то процесс самопроизвольно не протекает;
  
• 
  если dG = 0, то система находится в состоянии равновесия.
  

Характеристической функцией называется такая функция состояния системы, посредством которой или ее производных могут быть выражены в явной форме термодинамические свойства системы. Характеристическими функциями являются:

1. 
   внутренняя энергия U ,
   
2. 
   энтальпия H,
   
3. 
   изохорно-изотермический потенциал F,
   
4. 
   изобарно-изотермический потенциал G,
   
5. 
   энтропия S.
   

Определим значение частных производных основных характеристических функций.

Известно, что для любой функции

---