Файл: Контрольные вопросы для самопроверки знаний по разделу дисциплины физической химии Химическая термодинамика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 95
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
где
Из объединенного уравнения первого и второго закона термодинамики:
Дифференцируем выражение
Н = U + pV:
Вместо
Таким образом, из уравнения (6.14) следует, что
Запишем выражение полных дифференциалов dU и dH.
Сопоставляя уравнение (6.16) с уравнением (6.14) и уравнение (6.17) с уравнением (6.15) можно заключить, что
Эти соотношения показывают физический смысл частных производных внутренней энергии и энтальпии.
Запишем выражения для полных дифференциалов энергии Гельмгольца и энергии Гиббса:
Рассмотрим F как функцию от T и V, а Gкак функцию T и р. Их полные дифференциалы равны:
Сопоставляя эти выражения с уравнениями (6.5):
Изменение изохорного потенциала с изменением температуры при постоянном объеме определяется энтропией. Изменение изохорного потенциала с изменением объема при постоянной температуре определяется давлением.
Изменение изобарного потенциала с температурой при постоянном давлении определяется энтропией. Изменение изобарного потенциала с изменением давления при постоянной температуре определяется объемом.
Уравнения Гиббса-Гельмгольца. Запишем выражения для энергии Гельмгольца и энергии Гиббса:
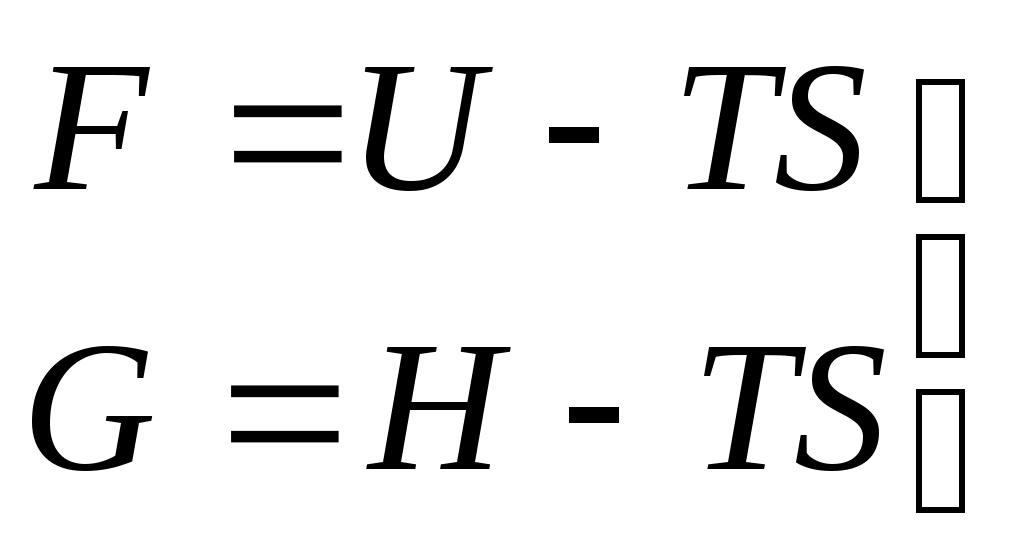 .
.Подставим в эти уравнения, вместо энтропии равные ей производные потенциалов, получаем соотношения:
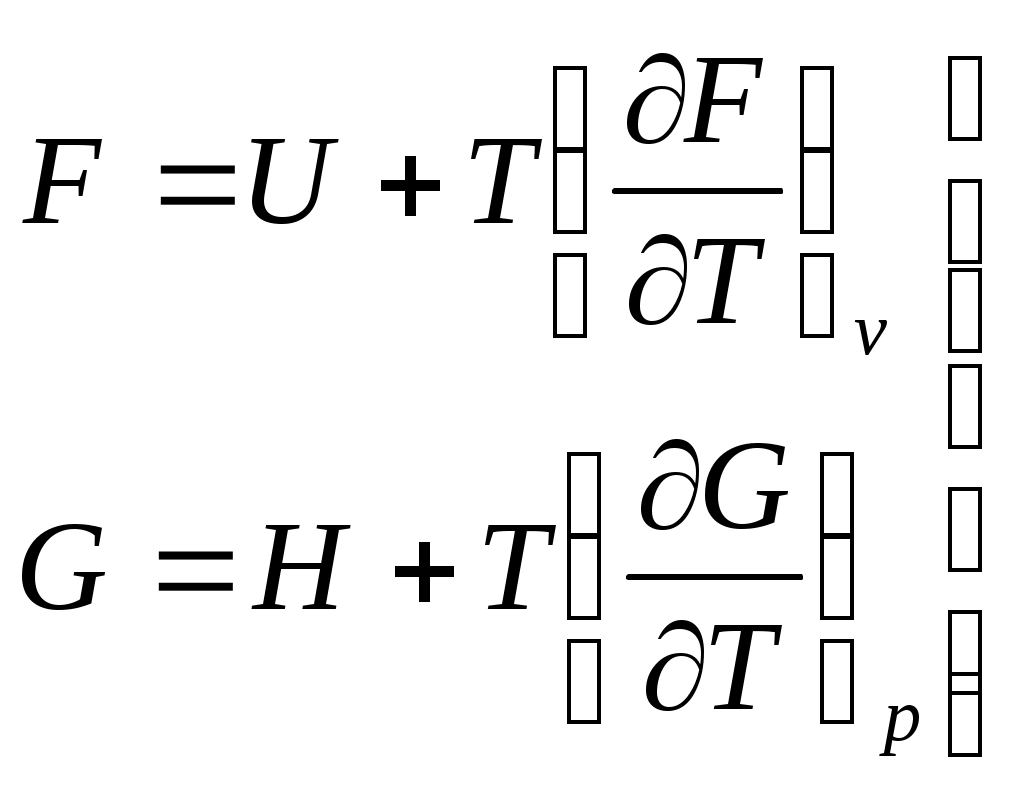 .
.Для изменения
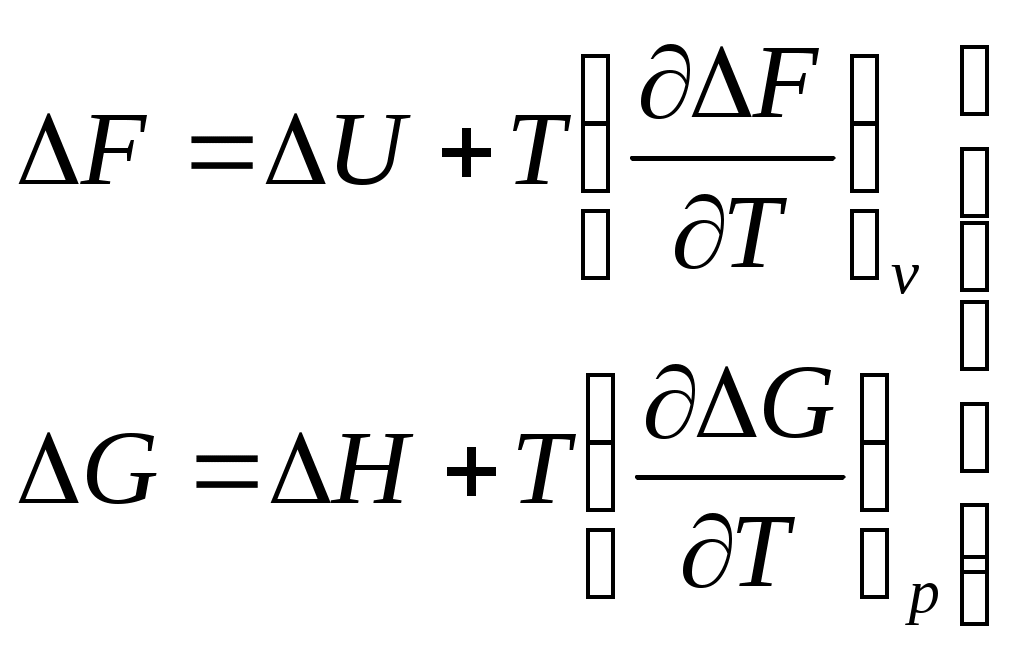 . (6.28, 6.29)
. (6.28, 6.29)Уравнения (6.28 и 6.29) - это уравнения Гиббса-Гельмгольца.
Химический потенциал. Для изучения растворов и гетерогенных систем, состоящих из 2-х и более веществ необходимо рассматривать системы, где состав и масса могут быть непостоянными вследствие химической реакции, испарения, кристаллизации и т.д. Изобарный потенциал является функцией не только
Т и р, но и количества n1, n2, n3,…, nj молей компонентов.
Химический потенциал
или
При
Математическое выражение условия равновесия системы с переменным числом молей компонентов:
Представим , что из фазы α в фазу β, переходит dn1 молей 1-го компонента.
| α  |
| β |
Условие фазового равновесия для 1-го компонента:
При фазовом равновесии химический потенциал каждого компонента во всех фазах одинаков.
Л е к ц и я 7
СТАТИСТИЧЕСКИЙ ХАРАКТЕР
ВТОРОГО ЗАКОНА ТЕРМОДИНАМИКИ
План лекции:
Статистический характер второго закона термодинамики. Термодинамическая вероятность состояния системы. Уравнение Больцмана-Планка. Границы применимости второго закона термодинамики.
Второй закон термодинамики можно назвать законом возрастания энтропии при самопроизвольном процессе в изолированной системе. В связи с этим очень важно выяснить физические причины необратимости реальных процессов, сопровождающихся возрастанием энтропии.
Смысл второго закона термодинамики можно понять более глубоко исходя из молекулярно-кинетической теории. Рассмотрим уравнение
Характер зависимости энтропии идеального газа от температуры и давления показывает, что энтропия S, может служить мерой беспорядка в расположении и движении молекул. Возрастание энтропии связано с самопроизвольным переходом вещества из состояния со строго упорядоченным расположением частиц в состояние с большим и наибольшим молекулярным беспорядком. Максимальной энтропии отвечало бы состояние газа с совершенно равномерным распределением хаотически движущихся частиц по объему. Однако, в каждый момент времени, в результате беспорядочного движения молекул, имеются местные отклонения от равномерного распределения: временное увеличение концентрации молекул в одних участках объема и уменьшение в других. Поэтому можно говорить о более или менее вероятных состояниях системы. Термин «вероятность состояния» равнозначен по смыслу понятию «беспорядок». Энтропия, является мерой вероятности состояния системы. Это открытие способствовало развитию статистической термодинамики.
Макросостоянием системы называется состояние, заданное термодинамическими параметрами. Это состояние из большого числа частиц. Микросостояние – это непосредственно ненаблюдаемое состояние молекул, атомов, ионов и др. частиц, характеризуемое координатами их положения в пространстве и скоростью их движения. В статистической термодинамике при подсчете вероятности состояния исходят из того, что одно макросостояние системы, например газа, при определенной температуре и давлении, может быть осуществлено большим числом микросостояний с любым распределением частиц по координатам и скоростям. Поскольку частицы газа постоянно и хаотически движутся, микросостояния постоянно чередуются. Однако любое микросостояние равновероятно. Число микросостояний, определяющих данное макросостояние, называется
термодинамической вероятностью состояния системы.
Допустим, что имеется всего три молекулы (обозначим цифрами), которые размещаются в двух ячейках фазового пространства (обозначим клетками). Рассмотрим макросостояние, когда в одной ячейке имеется 2 молекулы, а в другой одна. Данное макросостояние реализуется тремя перестановками молекул между ячейками, то есть тремя микросостояниями:
п
 ервое микросостояние
ервое микросостояние в
 торое микросостояние
торое микросостояниет
 ретье микросостояние
ретье микросостояниеЕсли в системе находится N молекул, то общее число перестановок будет N!. Поделив N! на число перестановок Ni! в каждой ячейке и исключив их тем самым из подсчета, получим термодинамическую вероятность:
где
Процесс выравнивания микросостояний, идущий в естественных условиях самопроизвольно и с возрастанием энтропии, приводит к росту термодинамической вероятности. Термодинамическая вероятность характеризует ту или иную степень беспорядка в сообществе частиц, из которых состоят тела системы. Термодинамическая вероятность, или вероятность состояния системы, оценивается энтропией.
Связь между энтропией и термодинамической вероятностью указывает статистическую природу второго закона термодинамики. Больцман Л. сделал допущение, что энтропия есть некоторая функция вероятности, S = f (W). В классической термодинамике доказывается, что в самопроизвольном процессе энтропии возрастает. С точки зрения статистической термодинамики этот же процесс сопровождается возрастанием вероятности W. При равновесии S и W принимают свои максимальные значения. Вид функции S = f (W) определяется уравнением Больцмана-Планка: