ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Размещено на http://www.allbest.ru/
Министерство образования и науки российской федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
Конспект лекций
по теме: «Функциональные ряды»
Волгодонск
1. Функциональные ряды
Определение:
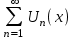 , где
, где 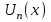 - функции переменной х называется функциональным рядом.
- функции переменной х называется функциональным рядом.При некоторых значениях х функциональный ряд сходится, при других значениях х – расходится.
Определение: Множество значений переменной х, при которых функциональный ряд
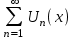 - сходится, называется областью сходимости функционального ряда. Задача нахождения области сходимости функционального ряда является весьма трудной, хотя для некоторых рядов область сходимости найти легко.
- сходится, называется областью сходимости функционального ряда. Задача нахождения области сходимости функционального ряда является весьма трудной, хотя для некоторых рядов область сходимости найти легко.Пример:
1)
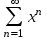
2)
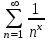
2. Равномерная сходимость функционального ряда
Определение: Функциональный ряд
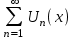 называется мажорируемым на [a;b], если существует сходящийся числовой ряд из
называется мажорируемым на [a;b], если существует сходящийся числовой ряд из 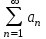 , так что
, так что 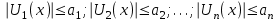 …при
…при 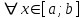 . При этом числовой ряд
. При этом числовой ряд 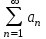 - мажоранта функционального ряда
- мажоранта функционального ряда 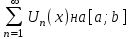 .
.Пример:
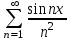
Как и числовой ряд ряд функциональный может быть записан в виде:
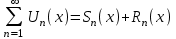 ; где
; где 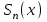 - n частичная сумма ряда,
- n частичная сумма ряда, 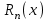 - n остаток ряда.
- n остаток ряда.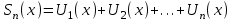
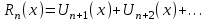
вычисление ряд тригонометрический тейлор
Определение:
 называется равномерно сходящимся на [a;b], если
называется равномерно сходящимся на [a;b], если 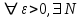 начиная с которого выполняется неравенство
начиная с которого выполняется неравенство 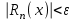 , при любом
, при любом , т.е
, т.е  - равномерно сходится на [a;b] если
- равномерно сходится на [a;b] если 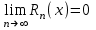 , для
, для  .
.Замечание: существуют сходящиеся функциональные ряды, которые не сходятся равномерно.
3. Признак Вейерштрасса о равномерной сходимости функционального ряда
Если функциональный ряд
 на [a;b] мажорируется сходящимся числовым рядом
на [a;b] мажорируется сходящимся числовым рядом 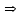
 равномерно сходится на этом отрезке.
равномерно сходится на этом отрезке.Свойства равномерно сходящегося функционального ряда:
Теорема 1: Если функциональный ряд
 ,составленный из непрерывных функций на [a;b], равномерно сходится на этом отрезке, то сумма ряда S(x) – тоже будет непрерывной функцией на [a;b].
,составленный из непрерывных функций на [a;b], равномерно сходится на этом отрезке, то сумма ряда S(x) – тоже будет непрерывной функцией на [a;b].Рассмотрим функциональный ряд
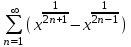
Этот ряд состоит из непрерывных степенных функций , n частичная сумма ряда
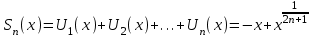
Вычислим сумму ряда:
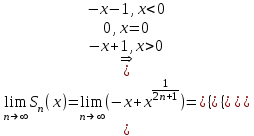

- сходится, но S(x) – является разрывной функцией.
Вывод: S(x) не сходится равномерно.
Теорема 2: Если функциональный
 равномерно сходится на [a;b]
равномерно сходится на [a;b] 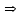 его можно почленно интегрировать на любом отрезке входящем в [a;b] условием интегрируемости является непрерывность функции
его можно почленно интегрировать на любом отрезке входящем в [a;b] условием интегрируемости является непрерывность функции  .
.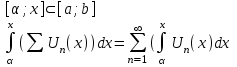
Пример:
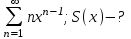
Теорема 3: Если функциональный
 равномерно сходится на [a;b] и ряд составленный из производных
равномерно сходится на [a;b] и ряд составленный из производных
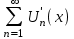 тоже равномерно сходится на [a;b]
тоже равномерно сходится на [a;b]  функциональный ряд можно почленно дифференцировать.
функциональный ряд можно почленно дифференцировать.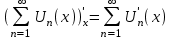
Пример:
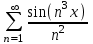
4. Степенные ряды
Определение: Степенным рядом называется ряд вида
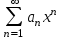 , где
, где 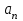 - коэффициент степенного ряда, зависит от n и не зависит от х.
- коэффициент степенного ряда, зависит от n и не зависит от х.Степенной ряд является частным случаем функционального ряда, поэтому естественно поставить вопрос об области сходимости степенного ряда и его равномерной сходимости. Ответ на вопрос какой вид имеет область сходимости степенного ряда дает теорема Абеля.
Теорема Абеля:
Если
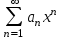 сходится в точке
сходится в точке 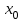
 он сходится во всех точках, удовлетворяющих неравенству
он сходится во всех точках, удовлетворяющих неравенству 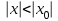 . Если
. Если 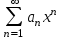 расходится в точке
расходится в точке 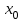
 он расходится во всех точках, удовлетворяющих неравенству
он расходится во всех точках, удовлетворяющих неравенству 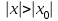 .
.Доказательство:
Пусть
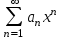 сходится в точке
сходится в точке 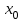
 будет сходится ряд
будет сходится ряд 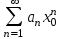
 по необходимому признаку сходимости
по необходимому признаку сходимости 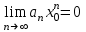
 числовая последовательность
числовая последовательность 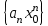 - ограничена, т.е существует число M>0, что
- ограничена, т.е существует число M>0, что 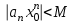 сразу для всех n.
сразу для всех n.Возьмем любое х удовл.
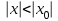 и рассмотрим
и рассмотрим 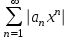 из абсолютных величин.
из абсолютных величин.Оценим общий член этого ряда:
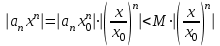
Ряд из членов геометрической прогрессии
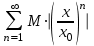 со знаменателем
со знаменателем 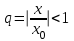 сходится
сходится  исходный
исходный  тоже сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда
тоже сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда
 сходится абсолютно.
сходится абсолютно.Пусть
 расходится в точке
расходится в точке .
.Возьмем любое х удовл.
 , нужно доказать, что
, нужно доказать, что  расходится при любом х, удовлетворяющем
расходится при любом х, удовлетворяющем  .
.Предположим противное:
 - сходится
- сходится  по 1 части доказательства он будет сходится в точке
по 1 части доказательства он будет сходится в точке  .
.Полученное противоречие доказывает теорему.
Конец доказательства.
Из теоремы Абеля
 что если степенной
что если степенной  сходится в
сходится в 
 он сходится в точке удовлетворяющей неравенству
он сходится в точке удовлетворяющей неравенству  :
: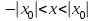
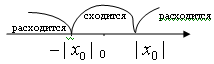
Рис. 1
Если
 расходится в точке
расходится в точке  , тогда он расходится
, тогда он расходится 
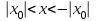
Вывод: существует интервал с центром в точке 0, радиусом R, внутри которого степенной ряд сходится, и вне которого расходится. Такой интервал называется интервалом сходимости степенного ряда, а R – радиусом сходимости степенного ряда. Укажем метод нахождения интервала сходимости.
5. Метод нахождения интервала сходимости степенного ряда
1) Дан
 , фиксируем х, получаем числовой ряд, и применим к ряду из модулей (для знакоположительности) признак Даламбера.
, фиксируем х, получаем числовой ряд, и применим к ряду из модулей (для знакоположительности) признак Даламбера.2) По признаку Даламбера вычисляем
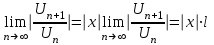
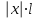 - чтобы ряд сходился по признаку Даламбера.
- чтобы ряд сходился по признаку Даламбера.3) Рассмотрим неравенство
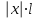 <1|:
<1|: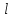
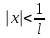
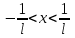 - интервал сходимости.
- интервал сходимости.4) На концах интервала сходимости, в точках
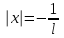 и
и 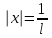 нужно провести дополнительное исследование.
нужно провести дополнительное исследование.Замечание: Частным случаем может оказаться, что
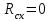 , тогда интервал сходимости вырождается в точку х=0
, тогда интервал сходимости вырождается в точку х=0 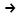 точка сходимости.
точка сходимости. 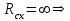 степенной ряд сходится на всей числовой оси и интервал сходимости
степенной ряд сходится на всей числовой оси и интервал сходимости 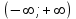
Примеры:
1)
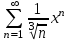
2)
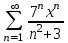
3)
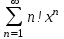
4)
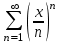
6. Равномерная сходимость степенного ряда
Теорема:
 равномерно сходится на любом отрезке от
равномерно сходится на любом отрезке от 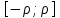 целиком лежащем внутри интервала сходимости.
целиком лежащем внутри интервала сходимости.Доказательство:
Степенной ряд
 сходится в точке
сходится в точке 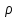
 сходится числовой ряд
сходится числовой ряд 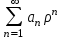
Возьмем
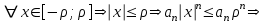 степенной ряд
степенной ряд  мажорируется на
мажорируется на 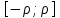 сходящимся числовым рядом
сходящимся числовым рядом