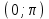ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 по признаку Вейерштрасса о равномерной сходимости степенного ряда, равномерно сходится на
по признаку Вейерштрасса о равномерной сходимости степенного ряда, равномерно сходится на 
Конец доказательства.
Следствия:
1) Т.к. члены степенного ряда являются непрерывными функциями, то внутри интервала сходимости сумма ряда тоже будет тоже непрерывной функцией.
2) Степенной ряд можно почленно интегрировать на любом
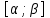 лежащем внутри интервала сходимости.
лежащем внутри интервала сходимости.3) Степенной ряд можно почленно дифференцировать внутри интервала сходимости, т.к. интервал сходимости ряда из производных будет точно таким же.
Доказательство:
 - степенной ряд.
- степенной ряд. - ряд из производных.
- ряд из производных.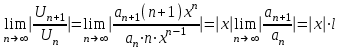
 <1 у ряда из производных тот же интервал сходимости.
<1 у ряда из производных тот же интервал сходимости.Конец доказательства.
7. Степенной ряд по степеням х-а
Рассмотрим
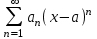
Сделаем замену: x-a=X


Найдём интервал сходимости полученного ряда, -R
Интервал сходимости полученного ряда имеет центр в точке А.
Пример:
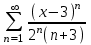
8. Ряды Тейлора
На I курсе рассматривалась формула Тейлора для функции f(x) n+1 раз дифференцируемая в окрестности точки
 .
.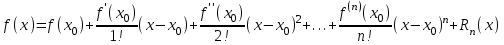
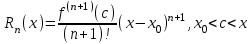
Если f(x) любое число раз дифференцируема в окрестности точки


 переходя к пределу
переходя к пределу 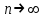 в формуле Тейлора получим:
в формуле Тейлора получим: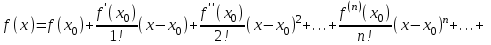
ряд стоящий в правой части равенства называется рядом Тейлора для функции f(x) по степеням
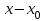 , а сама формула называется разложением функции f(x) в ряд Тейлора.
, а сама формула называется разложением функции f(x) в ряд Тейлора.Формально ряд Тейлора может быть получен для любой функции, но сходится к этой функции он будет только тогда, когда

Если этот предел
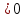 , то ряд либо расходится, либо сходится к совсем другой функции.
, то ряд либо расходится, либо сходится к совсем другой функции.9. Единственность разложения функции в ряд Тейлора
Теорема: Если функция f(x) разлагается в степенной ряд по степеням
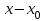 , то это обязательно ряд Тейлора.
, то это обязательно ряд Тейлора.Доказательство:
Пусть функция разлагается в степенной ряд вида:
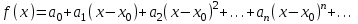
Найдём коэффициенты степенного ряда, Подставим
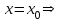
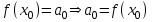
Продифференцируем 1 раз
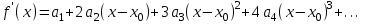
Подставим
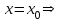
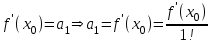
Продифференцируем 2 раз
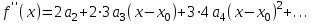
Подставим
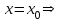
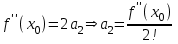
Продифференцируем 3 раз
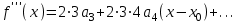
Подставим
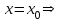
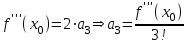
Аналогично покажем
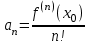
Коэффициенты степенного ряда совпадают с коэффициентами рядами Тейлора.
Конец доказательства.
10. Условия разложимости функции в ряд Тейлора
Определение: Семейство функций
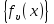 называется равномерно ограниченным на множестве D, если существует число M>0, что
называется равномерно ограниченным на множестве D, если существует число M>0, что 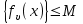 сразу для всех функций семейства и любого
сразу для всех функций семейства и любого 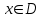 .
.Теорема: Пусть функция
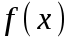 -любое количество раз дифференцируема в окрестности точки
-любое количество раз дифференцируема в окрестности точки
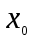 и семейство ее производных любого порядка равномерно ограничено в окрестности точки
и семейство ее производных любого порядка равномерно ограничено в окрестности точки 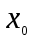 ,то функцию
,то функцию  можно разложить в ряд Тэйлора в окрестности точки
можно разложить в ряд Тэйлора в окрестности точки 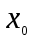 .
.Покажем что

Остаточный член

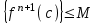 , где M>0 (т.к семейство производных равномерно ограничено)
, где M>0 (т.к семейство производных равномерно ограничено)Рассмотрим
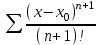
Можно показать по признаку Даламбера, что ряд сходится при любом х.
По необходимому признаку сходимости

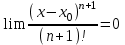
Рассмотрим
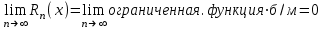
Конец доказательства.
11. Ряды Маклорена
Если в ряде Тейлора
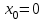 , то получим ряд Маклорена по степеням х.
, то получим ряд Маклорена по степеням х.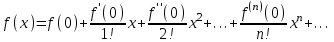
Остаточный член
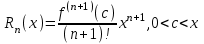
Получим разложение некоторых элементарных функций в ряд Маклорена и найдём интервалы сходимости этих рядов.
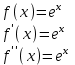
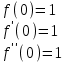
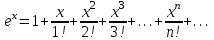 Интервал сходимости этого ряда найдем непосредственно по признаку Даламбера.
Интервал сходимости этого ряда найдем непосредственно по признаку Даламбера.Интервал сходимости
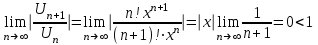
При любом х ряд сходится по признаку Даламбера.
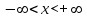 - интервал сходимости.
- интервал сходимости.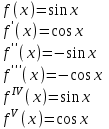
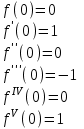
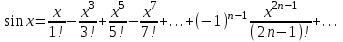
т.к семейство производных любого порядка равномерно ограничено
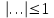 при
при 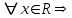 интервал сходимости
интервал сходимости 
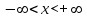
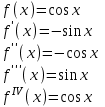
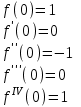
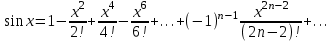
 - интервал сходимости.
- интервал сходимости.Биномиальное разложение
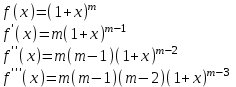
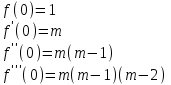
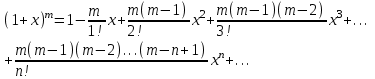
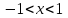 - интервал сходимости.
- интервал сходимости.f(x)=ln(1+x)
Воспользуемся предыдущим биномиальным разложением:
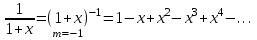
проинтегрируем почленно на отрезке
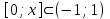
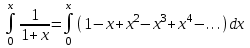
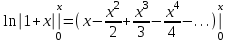
снимем модуль, т.к. 1+х>0
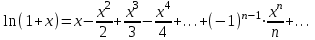
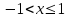 - можно показать.
- можно показать.f(x)=arctgx
воспользуемся биномиальным разложением и заменим
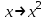
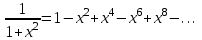
проинтегрируем на
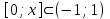
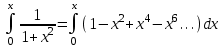
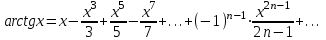
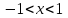
12. Приближенное вычисление с помощью рядов Тейлора и Маклорена
С помощью рядов Тейлора и Маклорена можно приближенно вычислять значения функций. Для этого функцию раскладывают в степенной ряд Тейлора и заменяем сумму ряда его частичной суммой. Возникающую при этом погрешность (остаточный член) оценивают следующим образом:
1) если ряд знакочередующийся, то последствию из теоремы Лейбница, для знакочередующихся рядов, остаточный член не превосходит модуля 1 отбрасываемого члена.
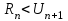
2) если ряд знакоположительный, то остаточный член оценивается непосредственно.
Примеры:
1)
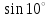
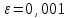
2)
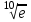
3)
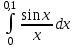
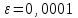
13. Тригонометрические ряды Фурье
Тригонометрическим рядом Фурье для функции f(x) на интервале от
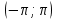 называется ряд вида:
называется ряд вида: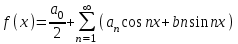 ,
, 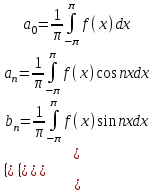
Условия разложимости:
Пусть f(x):
1) Периодическая с
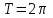
2) Кусочномонотонна
3) Ограничена на
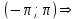 функцию f(x) можно разложить в ряд Фурье на
функцию f(x) можно разложить в ряд Фурье на 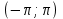 , который сходится к этой функции во всех точках непрерывности, в точках разрыва сумма ряда равна полусумме левого и правого предела функции.
, который сходится к этой функции во всех точках непрерывности, в точках разрыва сумма ряда равна полусумме левого и правого предела функции.Замечание: Основная трудность построения рядов Фурье в вычислении интегралов.
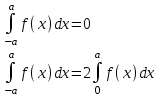
Пример:
Разложить функцию f(x)=x на
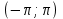 в тригонометрический ряд Фурье, сделать чертеж.
в тригонометрический ряд Фурье, сделать чертеж.14. Тригонометрический ряд Фурье от четных и нечетных функций и на интервале
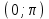
Если f(x) – четная

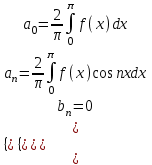
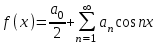 - ряд Фурье по косинусам.
- ряд Фурье по косинусам.Если f(x) – нечетная

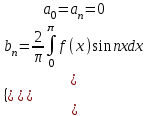
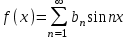 - ряд Фурье по синусам.
- ряд Фурье по синусам.Если функция f(x) определена на интервале
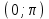 ее нужно продолжить (доопределить) на интервал
ее нужно продолжить (доопределить) на интервал 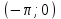 и только потом построить ряд Фурье. Продолжение функции на интервал
и только потом построить ряд Фурье. Продолжение функции на интервал 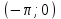 должно быть естественным, лучшее продолжение – четное или нечетное.
должно быть естественным, лучшее продолжение – четное или нечетное.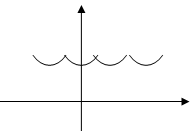
Рис. 2 Четное продолжение
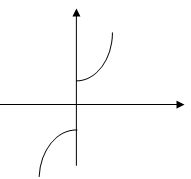
Рис. 3 Нечетное продолжение:
Пример:
Разложить функцию f(x)=1 на