МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»
Институт инженерной и экологической безопасности

(наименование института полностью)

20.03.01 Техносферная безопасность

(код и наименование направления подготовки / специальности)

Противопожарные системы

(направленность (профиль) / специализация)

ПрактическОе заданиЕ
по учебному курсу «Высшая математика 1»

Обучающегося	Коцага Станислав Олегович
	(И.О. Фамилия)
Группа	ТБбп-2006ас
Преподаватель	Курьянова Екатерина Александровна
	(И.О. Фамилия)

Тольятти 2023

РАЗДЕЛ № 1. ЛИНЕЙНАЯ АЛГЕБРА

Задача 1

Определить собственные значения и собственные векторы матрицы третьего порядка.



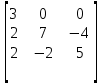
Решение

Дана матрица третьего порядка:



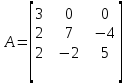
Найдем характеристическое уравнение:



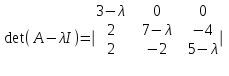
Вычислим определитель:



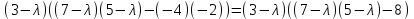
Раскроем скобки:

---

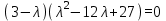
Теперь найдем собственные значения: λ₁ = 3, λ₂ = 3, λ₃ = 9

Теперь найдем собственные векторы для каждого собственного значения.

1) λ₁ = 3:



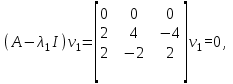
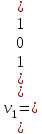
2) λ₂ = 3:



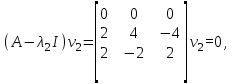
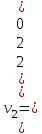
3) λ₃ = 9:



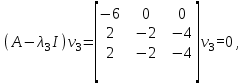
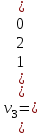
Собственные значения и соответствующие им собственные векторы:



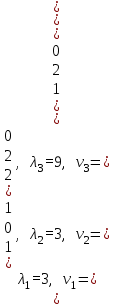
Таким образом, собственные значения матрицы A равны λ₁ = 3, λ₂ = 3 и λ₃ = 9, а соответствующие им собственные векторы равны

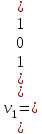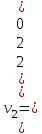, и .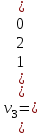

Задача 2

Доказать совместность системы и решить её тремя способами: по формулам Крамера, методом Гаусса и средствами матричного исчисления.



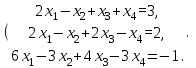
Решение

Дана система уравнений:



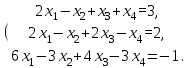
Метод Крамера

Для применения метода Крамера, вычислим определитель матрицы коэффициентов и проверим, не равен ли он нулю:



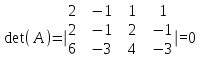
Определитель равен нулю, поэтому метод Крамера не может быть применен.

Метод Гаусса

Приведем систему уравнений к треугольному виду:



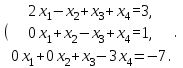
Теперь решим систему обратным ходом:







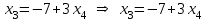
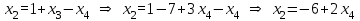
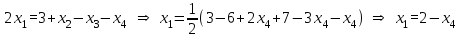
Таким образом, общее решение системы:



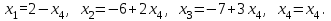
Матричный метод

Запишем систему уравнений в виде AX = B, где

---

A - матрица коэффициентов, X - вектор переменных, B - вектор свободных членов:



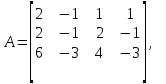
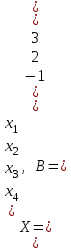
Так как определитель матрицы A равен нулю, мы не можем найти обратную матрицу и использовать формулу X = A^-1B. Вместо этого найдем ранг матрицы коэффициентов A и расширенной матрицы [A | B].



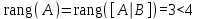
Так как ранг матрицы коэффициентов равен рангу расширенной матрицы и меньше числа переменных, система совместна и имеет бесконечно много решений. Решение совпадает с решением, найденным методом Гаусса:



Задача 3

Исследовать и найти общее решение системы линейных однородных уравнений



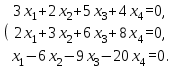
Решение

Исследуем и найдем общее решение системы линейных однородных уравнений:



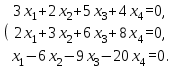
Сначала приведем систему уравнений к треугольному виду с помощью метода Гаусса:



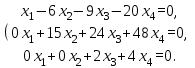
Теперь можно выразить x₃ и x₂ через x₄:





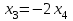
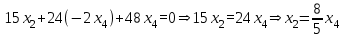
Подставим найденные выражения для x₂ и x₃ в первое уравнение и выразим x₁ через x₄:



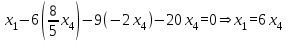
Общее решение системы имеет вид:



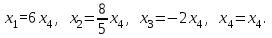
РАЗДЕЛ № 2. ВЕКТОРНАЯ АЛГЕБРА

Задача 1

Составить уравнение плоскости Р, проходящей через точку А перпендикулярно вектору . Написать ее общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить уравнение плоскости P₁, проходящей через точки А, В, С. Найти угол между плоскостями Р и P₁. Найти расстояние от точки D до плоскости Р.

Координаты точки А: (4; -3; -2)

---

Координаты точки В: (2; 2; 3)

Координаты точки С: (-1; -2; 3)

Координаты точки D: (2; -2; -3)

Решение

Даны точки A(4; -3; -2), B(2; 2; 3), C(-1; -2; 3) и D(2; -2; -3).

Плоскость P

1) Общее уравнение плоскости P имеет вид Ax + By + Cz = D. Найдем нормальный вектор к плоскости P, который совпадает с вектором :



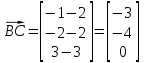
Теперь найдем D, подставив координаты точки A в уравнение плоскости:



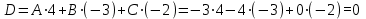
Таким образом, общее уравнение плоскости P имеет вид:



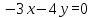
2) Нормальное уравнение плоскости имеет вид



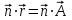
где 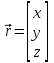и .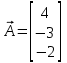

Тогда нормальное уравнение плоскости P:



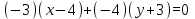
3) Уравнение плоскости в отрезках:



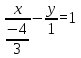
Плоскость P₁

4) Уравнение плоскости P₁, проходящей через точки A, B, C, можно найти через векторное произведение векторов 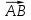и :





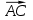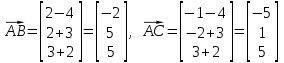
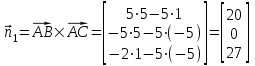
Теперь найдем D, подставив координаты точки A в уравнение плоскости:



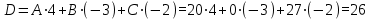
Таким образом, уравнение плоскости P₁ имеет вид:



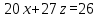
Угол между плоскостями P и P₁

5) Угол между плоскостями равен углу между их нормалям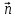и и 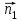Используем формулу скалярного произведения: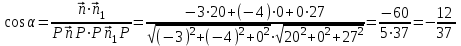

---

Таким образом, угол между плоскостями P и P₁ равен



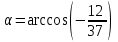
Расстояние от точки D до плоскости P

6) Расстояние от точки D(2; -2; -3) до плоскости P можно найти с помощью формулы:

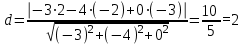
Таким образом, расстояние от точки D до плоскости P равно 2.

Задача 2

Прямая l задана в пространстве общими уравнениями. Написать её каноническое и параметрическое уравнения. Составить уравнение прямой l₁, проходящей через точку М параллельно прямой l, и вычислить расстояние между ними. Найти проекцию точки М на прямую l и точку пересечения прямой l и плоскости Р.

Общие уравнения прямой l:



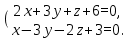
Координаты точки М(-1; 1; 0)

Общее уравнение плоскости P: x + 2y - z + 5 = 0

Решение

Даны общие уравнения прямой l:



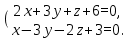
Точка M(-1; 1; 0) и плоскость P: x + 2y - z + 5 = 0.

Каноническое и параметрическое уравнения прямой l

1) Из уравнений системы найдем z в виде z = -2x - 3y - 6. Подставим это значение во второе уравнение:



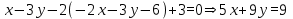
Из последнего уравнения получаем, что

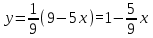
Теперь найдем z:



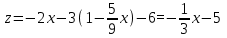
Таким образом, каноническое уравнение прямой l имеет вид:



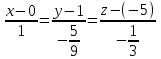
А параметрическое уравнение прямой l:



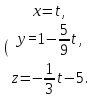
Уравнение прямой l₁ и расстояние между l и l₁

2) Прямая l₁ проходит через точку M(-1; 1; 0) и параллельна прямой l. Из параметрического уравнения l получаем направляющий вектор прямой l:



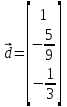
Тогда параметрическое уравнение прямой l₁:



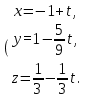
3) Для нахождения расстояния между прямыми l и l₁

---

Смотрите также файлы

• Проведения занятия.doc

• Реферат дисциплина Информационные и коммуникационные технологии часть 1 Тема Возможности WorldWideWeb при работе с информационными ресурсами студент группы гмноз1222(2).docx

• роль экологических факторов в развитии врожденных аномалий в центральном черноземье.ppt

• Задания для самоконтроля Цыганок Елена Ивановна, заместитель директора по врмбоу "сш 18", г. Ачинск Красноярский край.pdf

• з бетінше жмыс.docx