ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 25
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
воспользуемся формулой для расстояния между двумя параллельными прямыми:
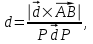
где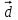 - направляющий вектор прямых,
- направляющий вектор прямых,
 - вектор между любой парой точек на каждой из прямых.
- вектор между любой парой точек на каждой из прямых.
Возьмем точку A(0; 1; -5) на прямой l и точку M(-1; 1; 0) на прямой l1:
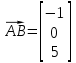
Теперь найдем векторное произведение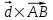 :
:
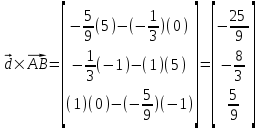
Теперь найдем норму векторов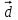 и
и 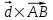 :
:
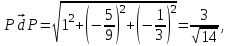
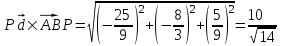
Теперь можно найти расстояние между прямыми l и l1:
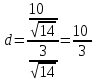
Проекция точки M на прямую l и точка пересечения прямой l и плоскости P
4) Проекция точки M на прямую l может быть найдена через формулу:
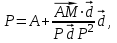
где A(0; 1; -5) - точка на прямой l, M(-1; 1; 0), а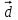 - направляющий вектор прямой l.
- направляющий вектор прямой l.
Подставим значения:
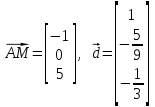
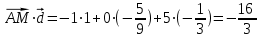
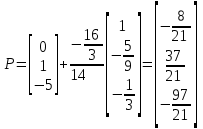
Таким образом, проекция точки M на прямую l равна
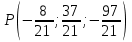
5) Точка пересечения прямой l и плоскости P удовлетворяет обоим уравнениям. Подставим параметрическое уравнение прямой l в уравнение плоскости P:
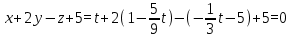
Решая это уравнение относительно t, получаем:
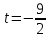
Теперь подставим значение t в параметрическое уравнение прямой l:
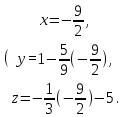
Таким образом, точка пересечения прямой
l и плоскости P равна:
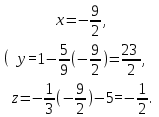
Точка пересечения прямой l и плоскости P равна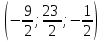
РАЗДЕЛ № 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Задача 1
Даны координаты вершин треугольника АВС. Составить уравнения сторон треугольника. Составить уравнения медианы, высоты и биссектрисы угла А, найти их длины. Составить уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам.
Координаты точки А (5; 0)
Координаты точки В (2; 2)
Координаты точки С (-2; 3)
Решение
1)Уравнения сторон треугольника можно найти, используя две точки на каждой стороне:
Уравнение стороны AB:
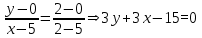
Уравнение стороны BC:
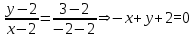
Уравнение стороны CA:
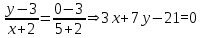
2) Уравнения медианы, высоты и биссектрисы угла A:
Медиана AM проходит через середину стороны BC. Найдем координаты точки M:
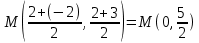
Теперь найдем уравнение медианы AM:
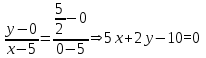
Высота AH перпендикулярна стороне BC. Уравнение высоты можно записать в виде:
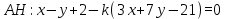
где k - коэффициент, который мы найдем, используя условие перпендикулярности:
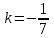
Теперь найдем уравнение высоты AH:
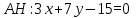
Биссектриса угла A делит угол между сторонами AB и CA пополам. Уравнение биссектрисы можно записать в виде:
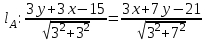
Упростим уравнение биссектрисы:
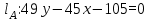
3) Длины медианы, высоты и биссектрисы угла A:
Длина медианы AM:
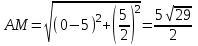
Длина высоты AH:
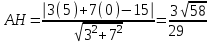
Длина биссектрисы
lA:
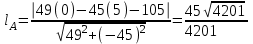
4) Уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам:
Прямая через вершину A и параллельная стороне BC:
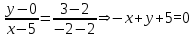
Прямая через вершину B и параллельная стороне AC:
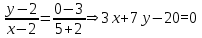
Прямая через вершину C и параллельная стороне AB:
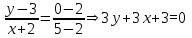
Задача 2
Координатам вершин пирамиды АВСD средствами векторной алгебры
найти:
1) длины ребер АВ и АС;
2) угол между ребрами АВ и АС;
3) площадь грани АВС;
4) проекцию вектора на
на  ;
;
5) объем пирамиды
Координаты точки А (2; 0; 3)
Координаты точки В (1; 0; 7)
Координаты точки С (0; 1; 3)
Координаты точки D (2; 2; 4)
Решение
1) Для нахождения длин ребер AB и AC воспользуемся формулой расстояния между двумя точками:
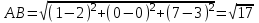
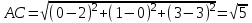
2) Чтобы найти угол между ребрами AB и AC, сначала найдем их векторы:
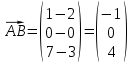
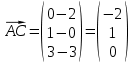
Теперь воспользуемся формулой для нахождения угла между двумя векторами:
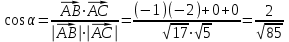
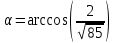
3) Для нахождения площади грани ABC используем векторное произведение и найдем площадь треугольника:
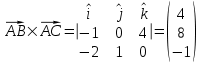
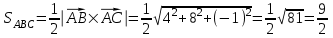
4) Найдем проекцию вектора на
на  :
:
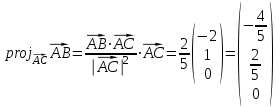
5) Для нахождения объема пирамиды ABCD используем скалярное произведение:
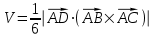
Сначала найдем вектор
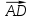 :
:
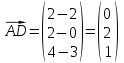
Теперь найдем скалярное произведение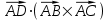
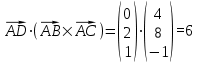
Теперь найдем объем пирамиды:
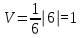
РАЗДЕЛ № 4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Задача 1
Построить графики функций
y = -2x2 + 3x + 2, y = ln(x- 4), y = sin 0,5x + 1, y = ln |x|
Решение
Даны функции:
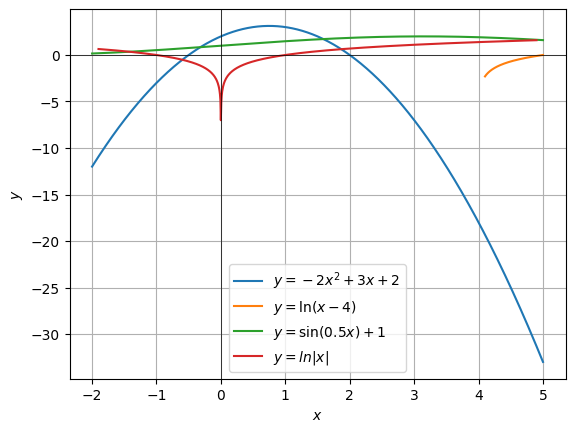
y = -2x2 + 3x + 2, y = ln(x- 4), y = sin 0,5x + 1, y = ln |x|
Создадим область определения функций, после чего вычислим значения функций и отобразим их на графиках. Ниже представлены графики заданных функций:
Задача 2
Записать уравнения кривых в полярных координатах и построить их
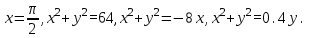
Решение
Запись уравнений кривых в полярных координатах:
При переходе к полярным координатам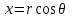 , поэтому
, поэтому 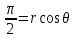 . Решая относительно r, получаем уравнение кривой:
. Решая относительно r, получаем уравнение кривой:
r=π/2cosθ
Здесь x2 + y2 = r2, поэтому уравнение кривой в полярных координатах:
r2=64
Перепишем уравнение, используя полярные координаты: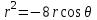 Решая относительно r, получаем уравнение кривой:
Решая относительно r, получаем уравнение кривой:
r=−8cosθ
Перепишем уравнение, используя полярные координаты:
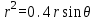 . Решая относительно r, получаем уравнение кривой:
. Решая относительно r, получаем уравнение кривой:
r=0,4sinθ
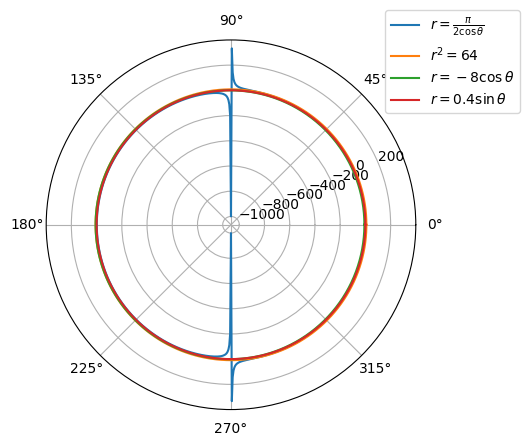
Теперь построим графики кривых в полярных координатах
Задача 3
Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1)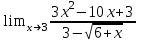
2)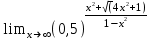
3)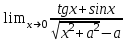
4)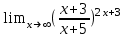
5)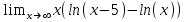
Решение
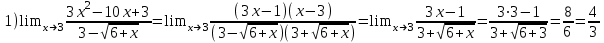
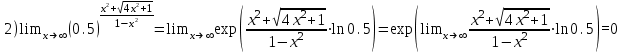
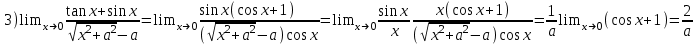
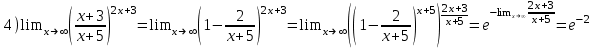
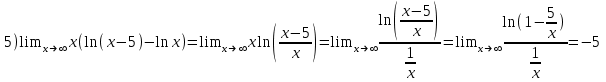
Задача 4
Исследовать на непрерывность функции, найти точки разрыва и определить их тип. Построить схематические графики функций.
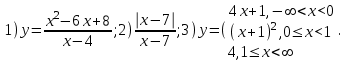
Решение
1)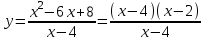
Функция непрерывна на всей области определения, кроме точки x = 4. В этой точке функция имеет разрыв первого рода.
2)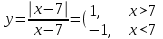
Функция непрерывна на всей области определения, кроме точки x = 7. В этой точке функция имеет разрыв второго рода.
3)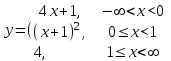
Функция непрерывна на всей области определения, кроме точек x = 0 и x = 1. В обеих точках функция имеет разрыв первого рода.
1) График функции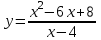 представляет собой параболу с разрывом в точке x = 4.
представляет собой параболу с разрывом в точке x = 4.
2) График функции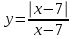 представляет собой две горизонтальные прямые y = 1 и y = -1 с разрывом в точке x = 7.
представляет собой две горизонтальные прямые y = 1 и y = -1 с разрывом в точке x = 7.
3) График функции состоит из трех частей: прямой 4x + 1 на интервале (-Ꝏ, 0), параболы (x + 1)2 на интервале [0, 1) и горизонтальной прямой y = 4 на интервале [1, Ꝏ). В точках x = 0 и x = 1 имеются разрывы первого рода.
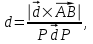
где
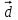 - направляющий вектор прямых,
- направляющий вектор прямых,  - вектор между любой парой точек на каждой из прямых.
- вектор между любой парой точек на каждой из прямых. Возьмем точку A(0; 1; -5) на прямой l и точку M(-1; 1; 0) на прямой l1:
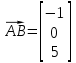
Теперь найдем векторное произведение
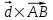 :
: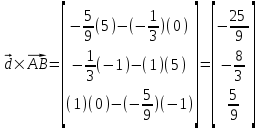
Теперь найдем норму векторов
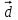 и
и 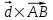 :
: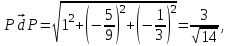
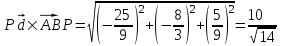
Теперь можно найти расстояние между прямыми l и l1:
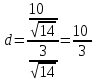
Проекция точки M на прямую l и точка пересечения прямой l и плоскости P
4) Проекция точки M на прямую l может быть найдена через формулу:
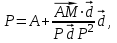
где A(0; 1; -5) - точка на прямой l, M(-1; 1; 0), а
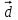 - направляющий вектор прямой l.
- направляющий вектор прямой l.Подставим значения:
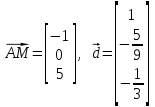
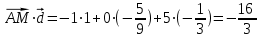
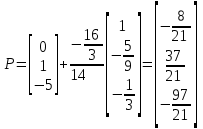
Таким образом, проекция точки M на прямую l равна
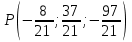
5) Точка пересечения прямой l и плоскости P удовлетворяет обоим уравнениям. Подставим параметрическое уравнение прямой l в уравнение плоскости P:
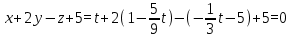
Решая это уравнение относительно t, получаем:
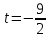
Теперь подставим значение t в параметрическое уравнение прямой l:
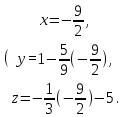
Таким образом, точка пересечения прямой
l и плоскости P равна:
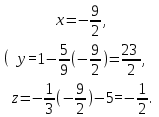
Точка пересечения прямой l и плоскости P равна
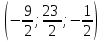
РАЗДЕЛ № 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Задача 1
Даны координаты вершин треугольника АВС. Составить уравнения сторон треугольника. Составить уравнения медианы, высоты и биссектрисы угла А, найти их длины. Составить уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам.
Координаты точки А (5; 0)
Координаты точки В (2; 2)
Координаты точки С (-2; 3)
Решение
1)Уравнения сторон треугольника можно найти, используя две точки на каждой стороне:
Уравнение стороны AB:
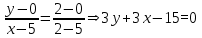
Уравнение стороны BC:
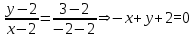
Уравнение стороны CA:
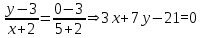
2) Уравнения медианы, высоты и биссектрисы угла A:
Медиана AM проходит через середину стороны BC. Найдем координаты точки M:
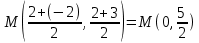
Теперь найдем уравнение медианы AM:
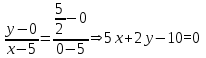
Высота AH перпендикулярна стороне BC. Уравнение высоты можно записать в виде:
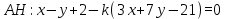
где k - коэффициент, который мы найдем, используя условие перпендикулярности:
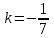
Теперь найдем уравнение высоты AH:
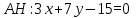
Биссектриса угла A делит угол между сторонами AB и CA пополам. Уравнение биссектрисы можно записать в виде:
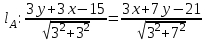
Упростим уравнение биссектрисы:
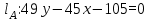
3) Длины медианы, высоты и биссектрисы угла A:
Длина медианы AM:
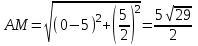
Длина высоты AH:
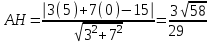
Длина биссектрисы
lA:
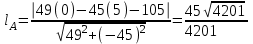
4) Уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам:
Прямая через вершину A и параллельная стороне BC:
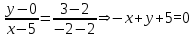
Прямая через вершину B и параллельная стороне AC:
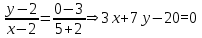
Прямая через вершину C и параллельная стороне AB:
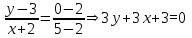
Задача 2
Координатам вершин пирамиды АВСD средствами векторной алгебры
найти:
1) длины ребер АВ и АС;
2) угол между ребрами АВ и АС;
3) площадь грани АВС;
4) проекцию вектора
 на
на  ;
; 5) объем пирамиды
Координаты точки А (2; 0; 3)
Координаты точки В (1; 0; 7)
Координаты точки С (0; 1; 3)
Координаты точки D (2; 2; 4)
Решение
1) Для нахождения длин ребер AB и AC воспользуемся формулой расстояния между двумя точками:
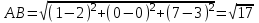
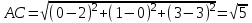
2) Чтобы найти угол между ребрами AB и AC, сначала найдем их векторы:
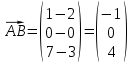
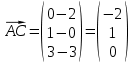
Теперь воспользуемся формулой для нахождения угла между двумя векторами:
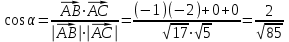
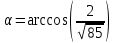
3) Для нахождения площади грани ABC используем векторное произведение и найдем площадь треугольника:
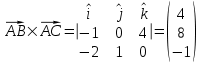
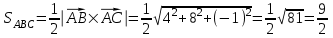
4) Найдем проекцию вектора
 на
на  :
: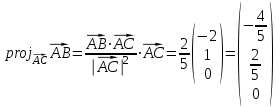
5) Для нахождения объема пирамиды ABCD используем скалярное произведение:
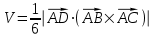
Сначала найдем вектор
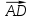 :
: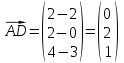
Теперь найдем скалярное произведение
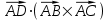
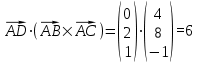
Теперь найдем объем пирамиды:
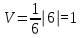
РАЗДЕЛ № 4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Задача 1
Построить графики функций
y = -2x2 + 3x + 2, y = ln(x- 4), y = sin 0,5x + 1, y = ln |x|
Решение
Даны функции:
y = -2x2 + 3x + 2, y = ln(x- 4), y = sin 0,5x + 1, y = ln |x|
Создадим область определения функций, после чего вычислим значения функций и отобразим их на графиках. Ниже представлены графики заданных функций:

Задача 2
Записать уравнения кривых в полярных координатах и построить их
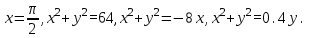
Решение
Запись уравнений кривых в полярных координатах:
-
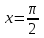 :
:
При переходе к полярным координатам
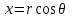 , поэтому
, поэтому 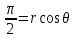 . Решая относительно r, получаем уравнение кривой:
. Решая относительно r, получаем уравнение кривой:r=π/2cosθ
-
x2 + y2 = 64:
Здесь x2 + y2 = r2, поэтому уравнение кривой в полярных координатах:
r2=64
-
x2 + y2 = -8x:
Перепишем уравнение, используя полярные координаты:
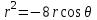 Решая относительно r, получаем уравнение кривой:
Решая относительно r, получаем уравнение кривой:r=−8cosθ
-
x2 + y2 = 0,4y:
Перепишем уравнение, используя полярные координаты:
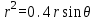 . Решая относительно r, получаем уравнение кривой:
. Решая относительно r, получаем уравнение кривой:r=0,4sinθ
Теперь построим графики кривых в полярных координатах

Задача 3
Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
1)
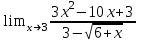
2)
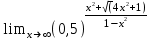
3)
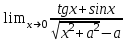
4)
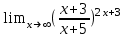
5)
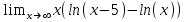
Решение
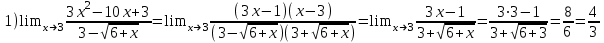
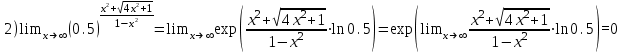
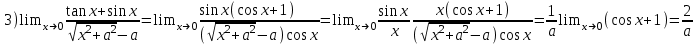
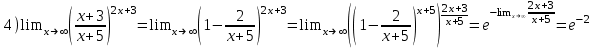
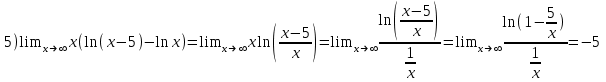
Задача 4
Исследовать на непрерывность функции, найти точки разрыва и определить их тип. Построить схематические графики функций.
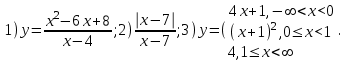
Решение
1)
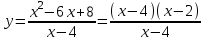
Функция непрерывна на всей области определения, кроме точки x = 4. В этой точке функция имеет разрыв первого рода.
2)
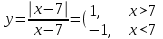
Функция непрерывна на всей области определения, кроме точки x = 7. В этой точке функция имеет разрыв второго рода.
3)
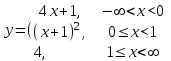
Функция непрерывна на всей области определения, кроме точек x = 0 и x = 1. В обеих точках функция имеет разрыв первого рода.
1) График функции
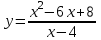 представляет собой параболу с разрывом в точке x = 4.
представляет собой параболу с разрывом в точке x = 4.2) График функции
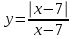 представляет собой две горизонтальные прямые y = 1 и y = -1 с разрывом в точке x = 7.
представляет собой две горизонтальные прямые y = 1 и y = -1 с разрывом в точке x = 7.3) График функции состоит из трех частей: прямой 4x + 1 на интервале (-Ꝏ, 0), параболы (x + 1)2 на интервале [0, 1) и горизонтальной прямой y = 4 на интервале [1, Ꝏ). В точках x = 0 и x = 1 имеются разрывы первого рода.