Файл: Практическая работа 2. Показатели надежности объекта Цель приобретение навыков расчета показателей надежности невосстанавливаемого объекта.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 644
Скачиваний: 15
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
t=3050 ч:
n(3050)=N0–Nср=400–150=250.
тогда
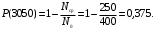
Частота отказа за 3000, 3100, 3050 часов (начало интервалов t=0):
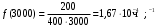
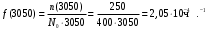
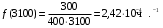
Интенсивность отказов за 3000, 3100, 3050 часов (начало интервалов t=0):
;
;
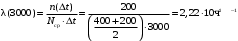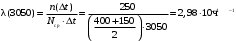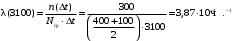
В интервале ∆t= 100 ч (начало интервала t=3000):
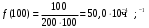
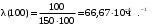
Задачи для решения
Задача 1. На испытание поставлено N0=1500 однотипных электронных ламп. За 5000 ч отказало n(t)=100 ламп. Требуется определитьза период 3000 ч вероятность безотказной работы P(t)и вероятность отказаQ(t).
Задача 2. На испытание поставлено N0=2000 однотипных приборов. За первые Δt1=3000 ч отказало 100 приборов, а за интервал времени Δt2=3000…4000 чотказало еще Δt2=100 приборов. Требуется определить частотуf(Δt2) и интенсивностьλ(Δt2) отказов приборов в промежутке времени ∆t = 3000–4000 ч.
Задача 3. Три однотипных объекта поставлены на испытания. За период наблюдения было зафиксировано по первому объекту 8 отказов, по второму – 10, третьему – 8. Наработка первого объекта составила t1=160 ч, второго t2=300 ч, третьего t3=240 ч. Определить наработку объектов на отказ.
Задача 4. Пусть время работы элемента до отказа подчинено экспоненциальному закону λ=2,5·10–5 ч–1. Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку до отказа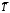
при t=1000, 2000, 3000 ч.
Задача 5. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрированоn(t)=10 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1000 ч. Определить среднюю наработку на отказ To
Задача 6. В аппаратуре было зафиксировано 10 отказов. Время восстановления составило:
t1=10 мин, t2=20 мин, t3=12 мин, t4=10 мин, t5=15 мин, t6=25 мин, t7=25 мин, t8=30 мин.
Требуется определить среднее время восстановления аппаратуры tв.
Задача 7. Аппаратура имела среднюю наработку на отказ То=75 ч и среднее время восстановления tв=1,2 ч. Требуется определить коэффициент готовности Кг.
Задача 8. Известно, что интенсивность отказов λ= 0,01 ч–1, а среднее время восстановления tв=5 ч. Требуется вычислить коэффициент готовности. Закон распределения экспоненциальный.
Задача 9. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Тэ=9010 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило tв=50 ч. Время проведения регламента составляет tо=10 ч. Суммарное времяtр, затраченное на ремонтные работы за период эксплуатации составляет 10 суток.
Задача 10. На испытание поставлено N0=500 изделий. За время t=3000 ч отказало n(3000)=100 изделий, за интервал ∆t=100 ч отказало n(∆t)=50 изделий. Требуется определить вероятность безотказной работы P(t), частоту отказовf(t) и интенсивность отказовλ(t) за 3000, 3100, 3050 часов, частоту интенсивность λ(t) отказов в интервале 3000…3100 часов.
n(3050)=N0–Nср=400–150=250.
тогда
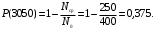
Частота отказа за 3000, 3100, 3050 часов (начало интервалов t=0):
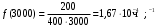
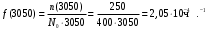
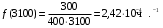
Интенсивность отказов за 3000, 3100, 3050 часов (начало интервалов t=0):
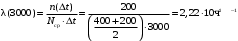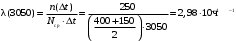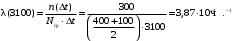
; ; В интервале ∆t= 100 ч (начало интервала t=3000):
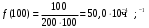
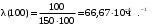
Задачи для решения
Задача 1. На испытание поставлено N0=1500 однотипных электронных ламп. За 5000 ч отказало n(t)=100 ламп. Требуется определитьза период 3000 ч вероятность безотказной работы P(t)и вероятность отказаQ(t).
Задача 2. На испытание поставлено N0=2000 однотипных приборов. За первые Δt1=3000 ч отказало 100 приборов, а за интервал времени Δt2=3000…4000 чотказало еще Δt2=100 приборов. Требуется определить частотуf(Δt2) и интенсивностьλ(Δt2) отказов приборов в промежутке времени ∆t = 3000–4000 ч.
Задача 3. Три однотипных объекта поставлены на испытания. За период наблюдения было зафиксировано по первому объекту 8 отказов, по второму – 10, третьему – 8. Наработка первого объекта составила t1=160 ч, второго t2=300 ч, третьего t3=240 ч. Определить наработку объектов на отказ.
Задача 4. Пусть время работы элемента до отказа подчинено экспоненциальному закону λ=2,5·10–5 ч–1. Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку до отказа
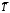при t=1000, 2000, 3000 ч.Задача 5. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрированоn(t)=10 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1000 ч. Определить среднюю наработку на отказ To
Задача 6. В аппаратуре было зафиксировано 10 отказов. Время восстановления составило:
t1=10 мин, t2=20 мин, t3=12 мин, t4=10 мин, t5=15 мин, t6=25 мин, t7=25 мин, t8=30 мин.
Требуется определить среднее время восстановления аппаратуры tв.
Задача 7. Аппаратура имела среднюю наработку на отказ То=75 ч и среднее время восстановления tв=1,2 ч. Требуется определить коэффициент готовности Кг.
Задача 8. Известно, что интенсивность отказов λ= 0,01 ч–1, а среднее время восстановления tв=5 ч. Требуется вычислить коэффициент готовности. Закон распределения экспоненциальный.
Задача 9. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Тэ=9010 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило tв=50 ч. Время проведения регламента составляет tо=10 ч. Суммарное времяtр, затраченное на ремонтные работы за период эксплуатации составляет 10 суток.
Задача 10. На испытание поставлено N0=500 изделий. За время t=3000 ч отказало n(3000)=100 изделий, за интервал ∆t=100 ч отказало n(∆t)=50 изделий. Требуется определить вероятность безотказной работы P(t), частоту отказовf(t) и интенсивность отказовλ(t) за 3000, 3100, 3050 часов, частоту интенсивность λ(t) отказов в интервале 3000…3100 часов.