Файл: Решение типового варианта Задание I.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 35

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Элементы математической статистики
Решение типового варианта

Задание I

В результате эксперимента получены данные, записанные в виде статистического ряда:

Требуется:

  1. записать значения результатов эксперимента в виде вариационного ряда;

  2. найти размах варьирования и разбить его на ряд частичных интервалов;

  3. построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;

  4. найти числовые характеристики выборки (математическое ожидание, дисперсию, среднее квадратическое отклонение);

  5. приняв в качестве нулевой гипотезу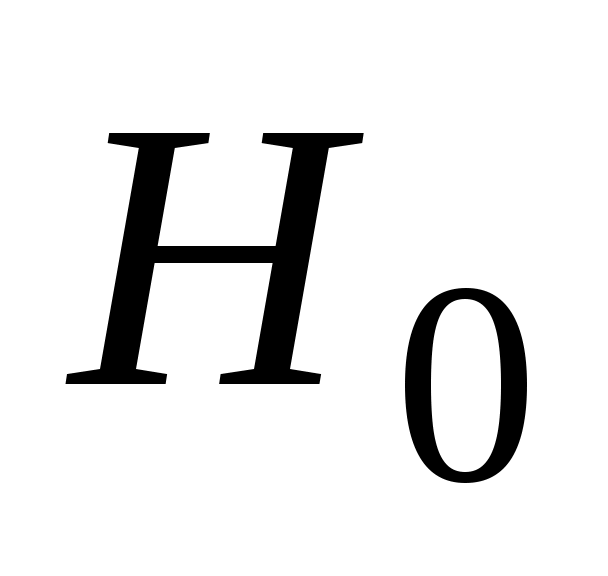 : генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить её, критерием Пирсона при уровне значимости ;

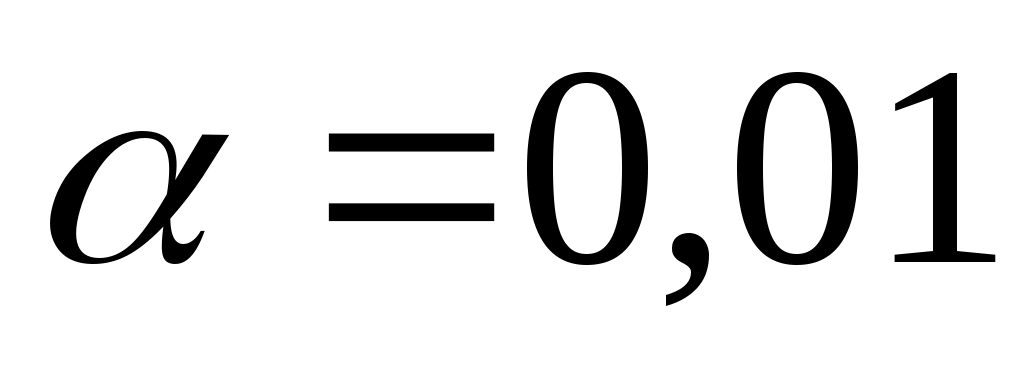  6. найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при надежности .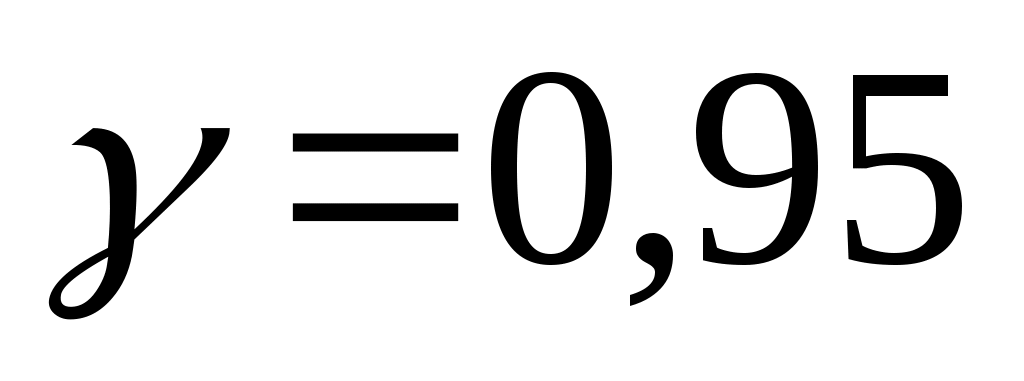




44,8
46,2
45,6
44,0
46,4
45,2
46,7.
45,4
45,3
46,1

44,3
45,3
45,6
46,7
44,5
46,0
45,7
45,0
46,4
45,9

44,4
45,4
46,1
43,4
46,5
45,9
43,9
45,7
47,1
44,9

43,8
45,6
45,2
46,4
44,2
46,5
45,7
44,7
46,0
45,8

44,3
45,5
46,7
44,9
46,2
46,7
44,6
46,0
45,4
45,0

45,4
45,3
44,1
46,6
44,8
45,6
43,7
46,8
45,2
46,1

44,5
45,4
45,1
46,2
44,2
46,4
45,7
43,9
47,2
45,0

43,9
45,6
44,9
44,5
46,2
46.7
44,3
46,1
47,7
45,8

45,6
45,2
44,2
46,0
44,7
46,5
43,5
45,4
47,1
44,0

46,2
44,2
45,5
46,0
45,7
46,4
44,6
47,0
45,2
46,9



Решение:

1). Располагаем значение результатов эксперимента в порядке возрастания, т.е. записываем вариационный ряд:


43,4
43,5
43,7
43,8
43,9
43,9
43,9
44,0
44,0
44,1

44,2
44,2
44,2
44,3
44,3
44,3
44,4
44,5
44,5
44,5

44,6
44,6
44,7
44,7
44,8
44,8
44,8
44,9
44,9
44,9

45,0
45,0
45,1
45,2
45,2
45,2
45,2
45,2
45,3
45,3

45,3
45,4
45,4
45,4
45,4
45,4
45,4
45,5
45,5
45,6

45,6
45,6
45,6
45,6
45,7
45,7
45,7
45,7
45,7
45,7

45,8
45,8
45,9
45,9
46,0
46,0
46,0
46,0
46,0
46,0

46,1
46,1
46,1
46,1
46,2
46,2
46,2
46,2
46,2
46,4

46,4
46,4
46,4
46,4
46,5
46,5
46,5
46,6
46,7
46,7

46,7
46,7
46,7
46,8
46,9
47,0
47,1
47,1
47,2
47,7


2). Находим размах варьирования:
.

Иногда для определения данных интервала используют формулу , где - объем выборки. За величину частичного интервала принимается некоторое удобное число, ближайшее к полученному . Число таких интервалов определяется формулой . В качестве границы первого интервала можно выбрать значение . Тогда границы следую­щих частичных интервалов вычисляем по формуле , где принимает значения от 1 до .

В нашем примере . Объём выборки , тогда . Примем за . Следовательно, разобьем наш вариационный ряд на интервалов.

Находим середины интервалов: . Подсчитываем число значений результатов эксперимента, по­павших в каждый интервал, т.е. находим частоты интервалов .Далее вычисляем относительные частоты и их плотности . Все полученные результаты помещаем в таблицу (табл. 1).

Таблица 1.

Номер

частичного ин­тервала i
Границы

интервала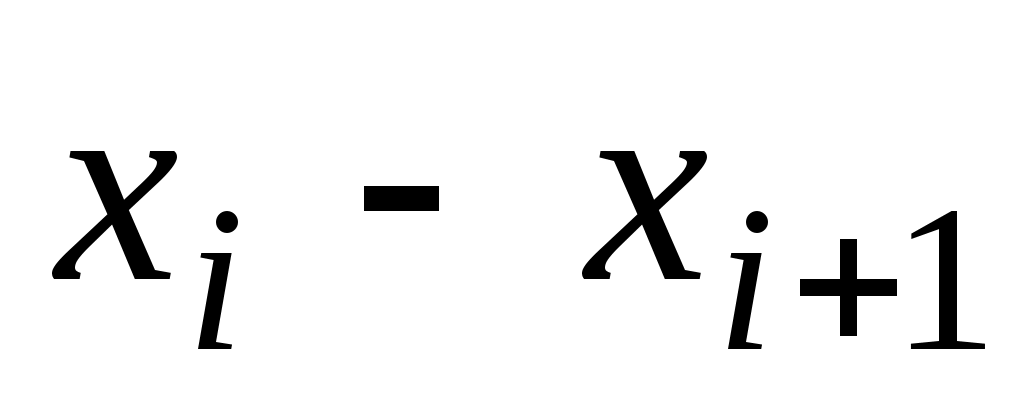
Середина интервала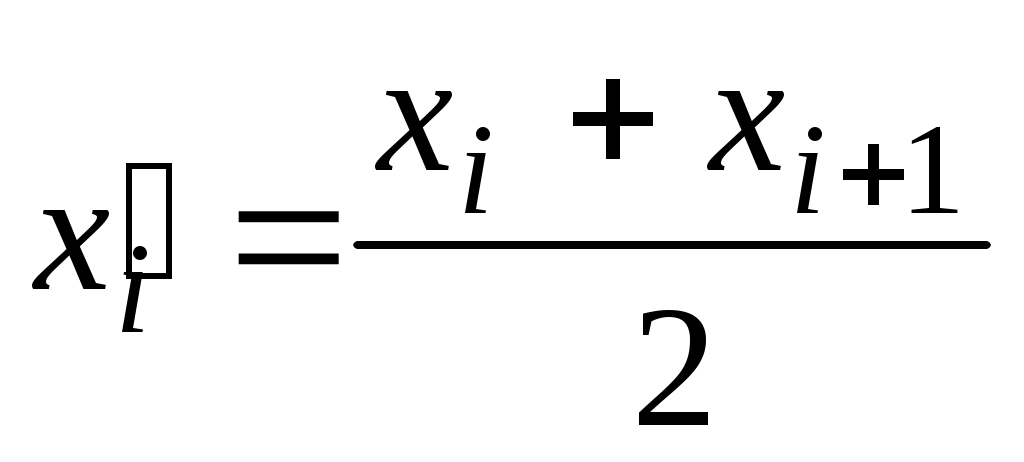
Частота

интер­вала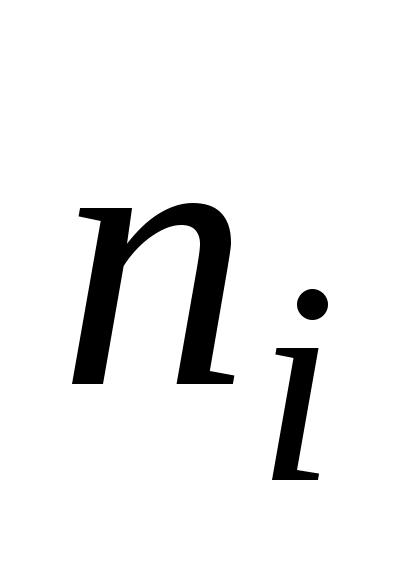

Относитель­ная частота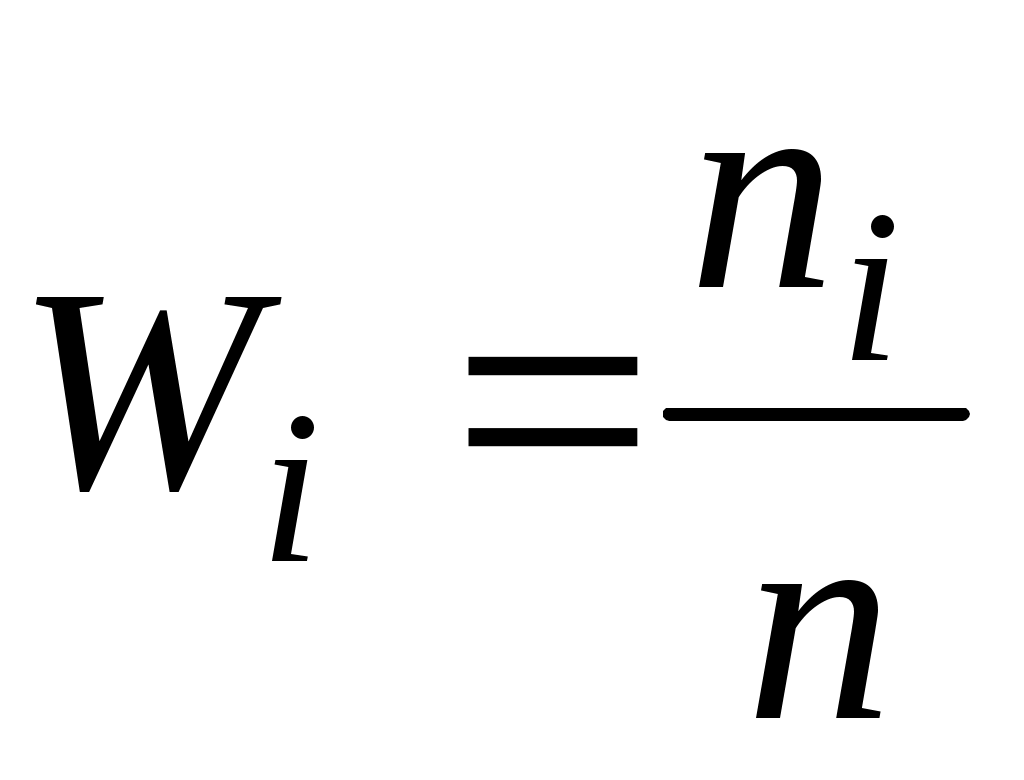

Плотность относитель-

ной частоты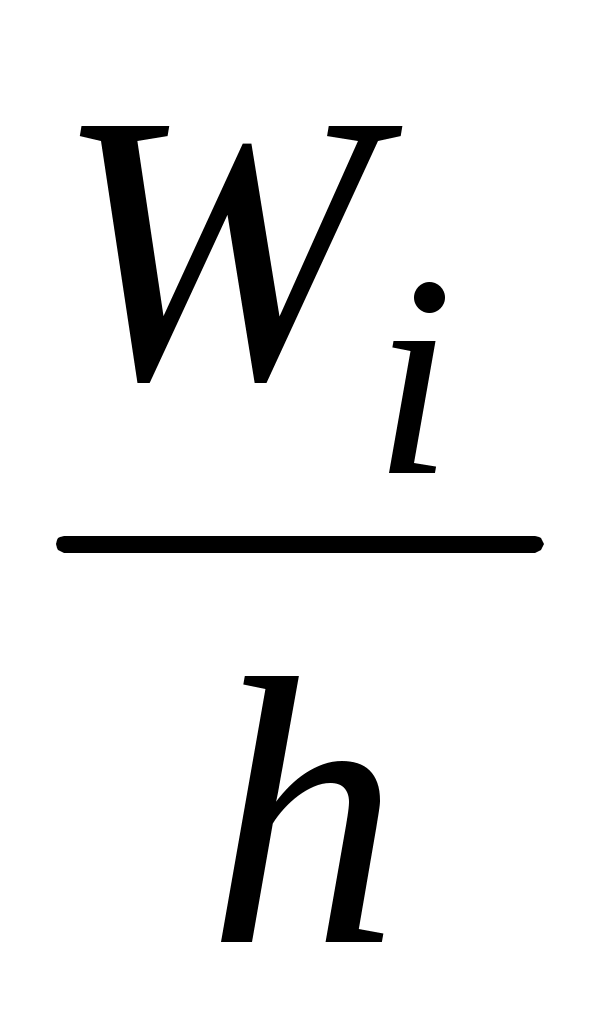



1
43,40 – 43,96
43,68
7
0,07
0,13

2
43,96 – 44,52
44,24
13
0,13
0,23

3
44,52 – 45,08
44,80
12
0,12
0,21

4
45,08 – 45,64
45,36
22
0,22
0,39

5
45,64 – 46,20
45,92
25
0,25
0,45

6
46,20 – 46,76
46,48
14
0,14
0,25

7
46,76 – 47,32
47,04
6
0,06
0,11

8
47,32 – 47,88
47,60
1
0,01
0,02






–
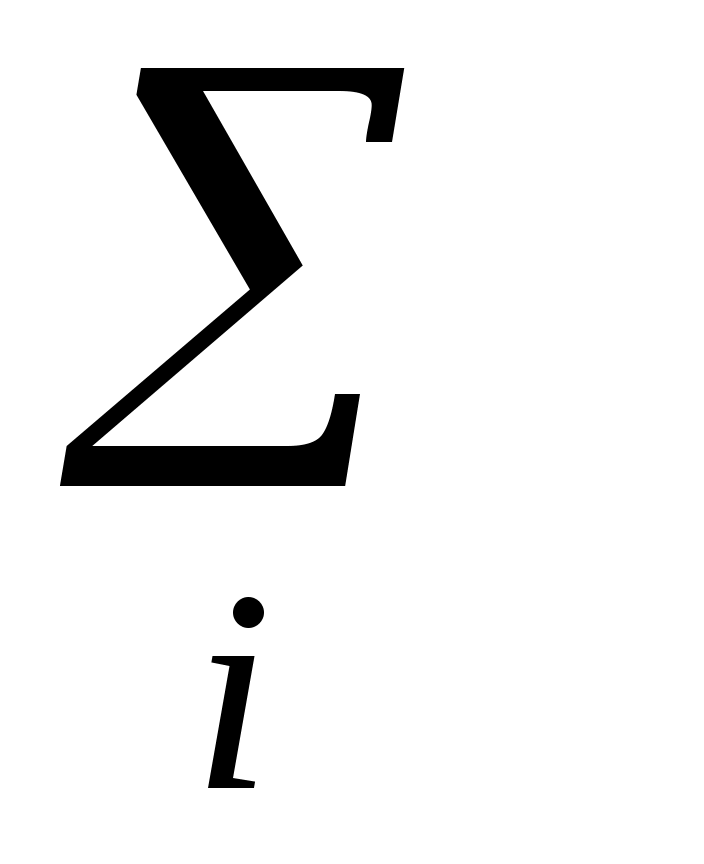
100
–




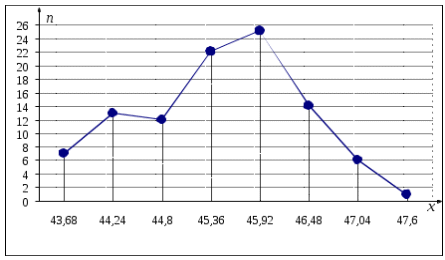
3). Строим полигон частот – ломанную линию, отрезки которой соединяют точки , , …, (рис. 1) и гистограмму относительных частот – ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы, длиною , а высоты равны плотности относительной частоты (рис.2).



Рис. 1. Полигон частот



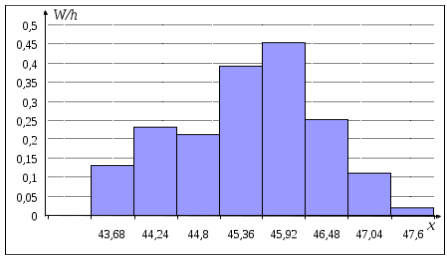
Рис.2. Гистограмма относительных частот

Найдем значения эмпирической функции распределения (функции распределения выборки) – функции, определяющей для каждого значения относительную частоту события .

Итак, по определению,

,

где - число вариант, меньших ; - объём выборки.

, , ,

, , ,

, , .

Строим график эмпирической функции распределения (рис. 3).



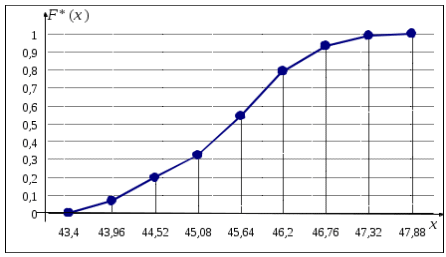
Рис. 3. График эмпирической функции распределения

Смотрите также файлы