ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 38
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
4). Находим выборочное среднее:
и выборочную дисперсию:
.Для этого составляем расчетную таблицу (табл. 2).
Таблица 2.
 | Границы интервала  | Середина интервала  | Частота интервала  |  |  |  |
| 1 | 43,40 – 43,96 | 43,68 | 7 | 305,76 | 1907,94 | 13355,60 |
| 2 | 43,96 – 44,52 | 44,24 | 13 | 575,12 | 1957,18 | 25443,31 |
| 3 | 44,52 – 45,08 | 44,80 | 12 | 537,60 | 2007,04 | 24084,48 |
| 4 | 45,08 – 45,64 | 45,36 | 22 | 997,92 | 2057,53 | 45265,65 |
| 5 | 45,64 – 46,20 | 45,92 | 25 | 1148,00 | 2108,65 | 52716,16 |
| 6 | 46,20 – 46,76 | 46,48 | 14 | 650,72 | 2160,39 | 30245,47 |
| 7 | 46,76 – 47,32 | 47,04 | 6 | 282,24 | 2212,76 | 13276,57 |
| 8 | 47,32 – 47,88 | 47,60 | 1 | 47,60 | 2265,76 | 2265,76 |
 | | – | 100 | 4544,96 | – | 206653 |
Из нее получаем:
, 
, 
.Несмещённой называют статистическую оценку
, математическое ожидание которой равно оцениваемому параметру 
при любом объёме выборки.Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру.
Выборочная дисперсия является смещенной оценкойгенеральной дисперсии, а исправленная дисперсия - несмещенной оценкой:
, 
.5). Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия:
(«хи квадрат») К. Пирсона, Колмагорова, Фишера, Смирнова и др. По условию задачи нам необходимо использовать критерий Пирсона, правило применения которого сводится к следующему:
-
вычислить теоретические частоты, затем наблюдаемое значение критерия по формуле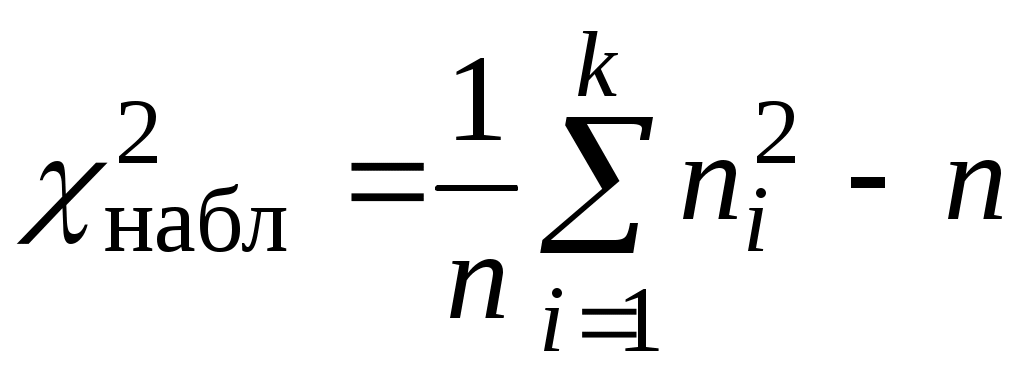
; -
по таблице критических точек распределения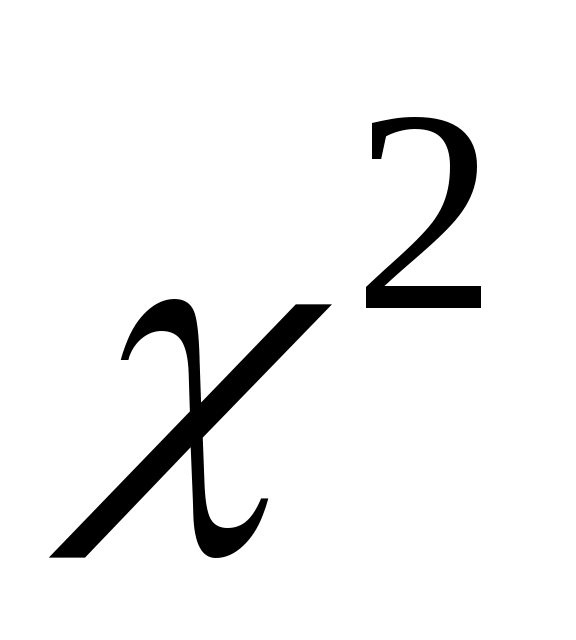 , по заданному уровню значимости 
и числу степеней свободы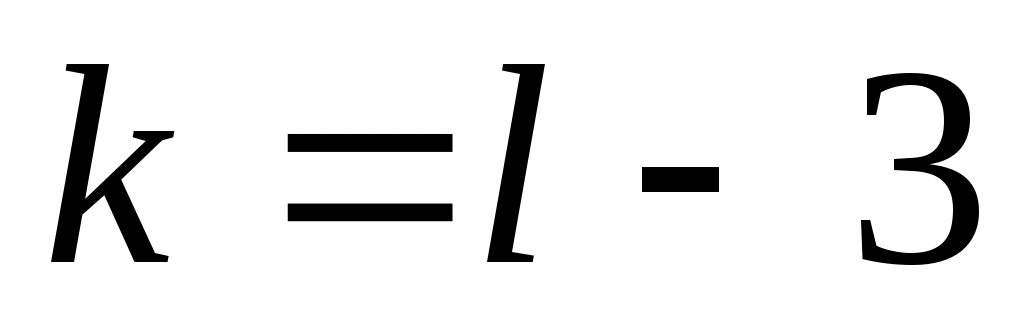 
, где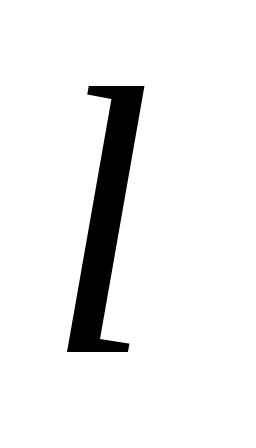 
– число интервалов, найти критическую точку 
; -
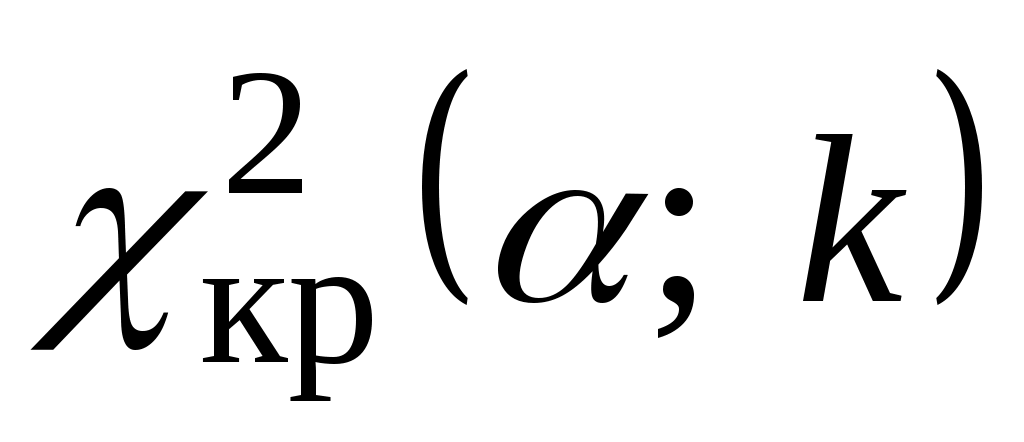если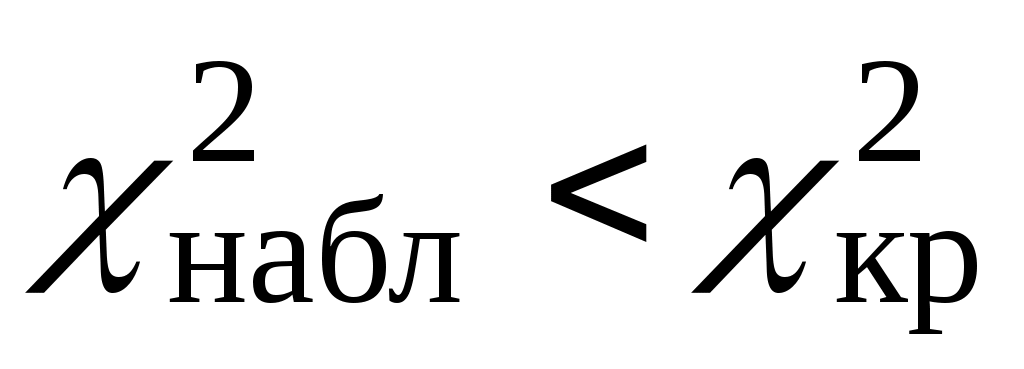
– нет оснований отвергать нулевую гипотезу;
если
– нулевую гипотезу отвергают.Согласно критерию Пирсона необходимо сравнить эмпирические и теоретические частоты. Эмпирические частоты даны. Найдем теоретические частоты. Для этого пронумеруем
,т.е. перейдем к случайной величине 
и вычислим концы интервалов: 
и 
. Наименьшее значение 
положим стремящимся к 
, а наибольшее – 
, стремящимся к 
. Результаты занесем в таблицу (табл. 3). Число наблюдений в отдельных интервалах должно быть достаточно большим (рекомендуется иметь в каждом интервале не менее 5-10 наблюдений). Если в отдельных интервалах очень малы, следует объединить интервалы. Длины интервалов могут быть различными. В соответствии с этим число исходных интервалов может быть уменьшено. Так как 
, то последний девятый интервал объединим с восьмым и получим интервал 
с частотой 
. Таблица 3.
-
Границы интервала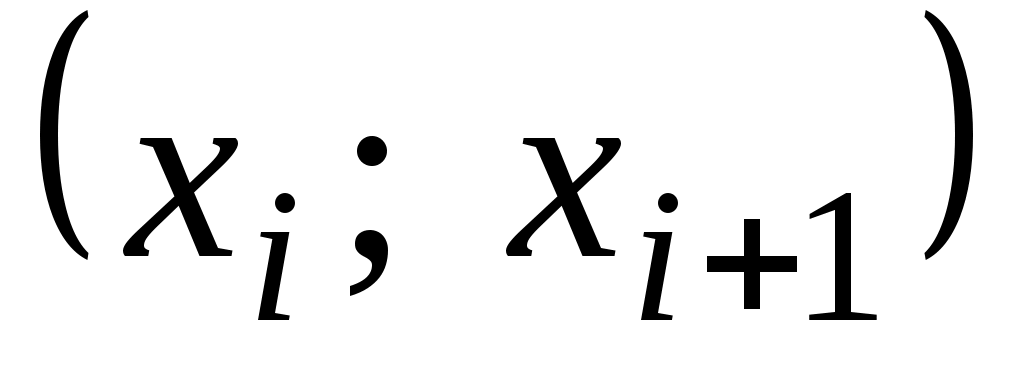
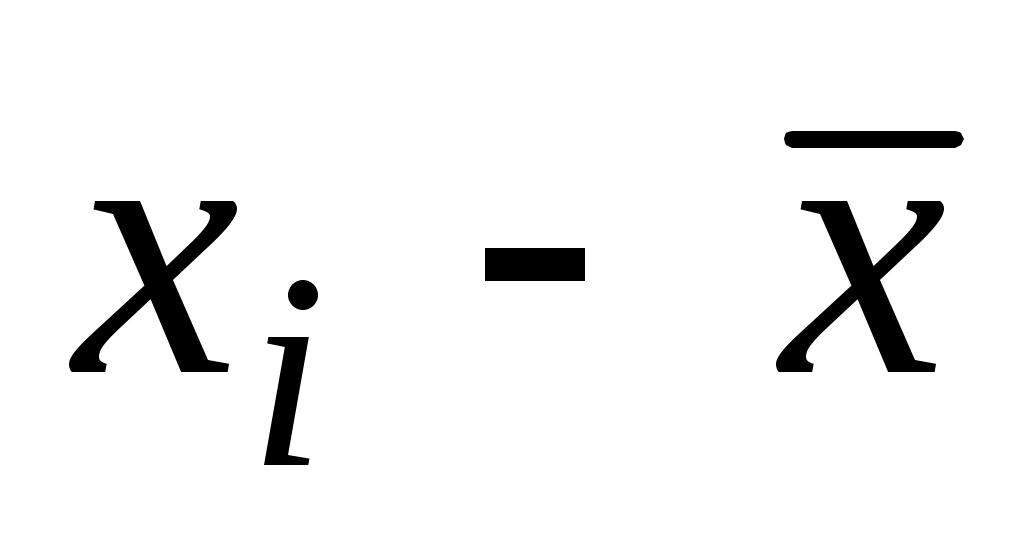
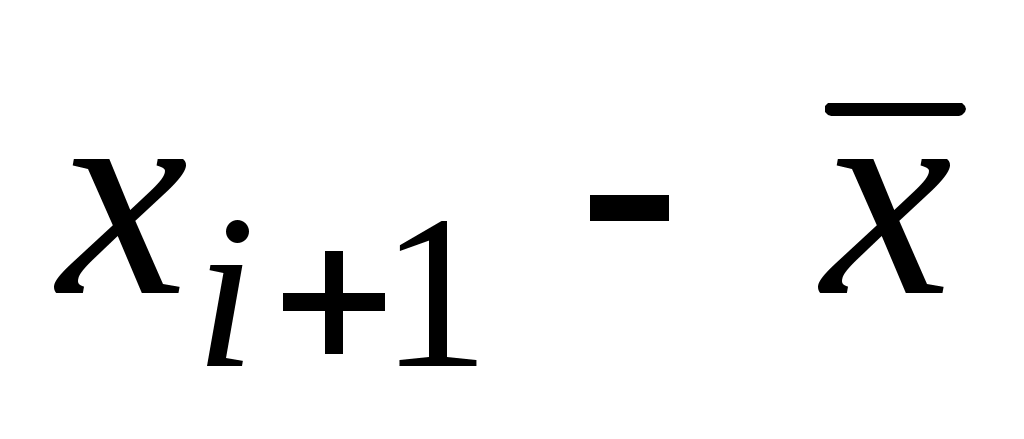
Границы интервала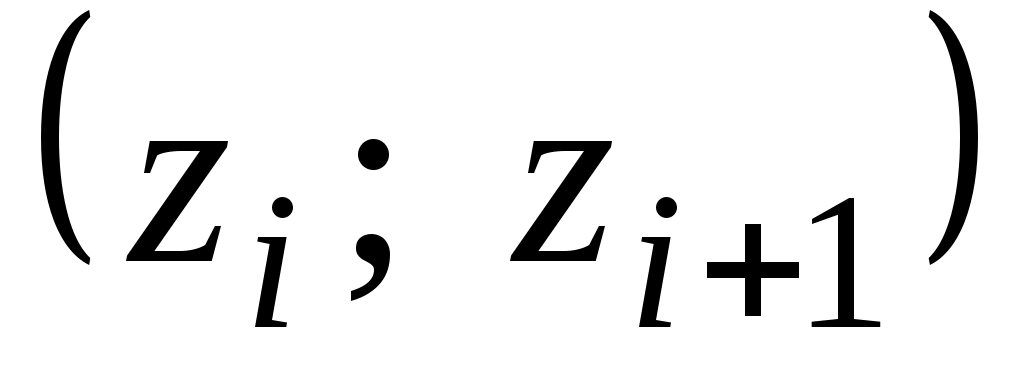
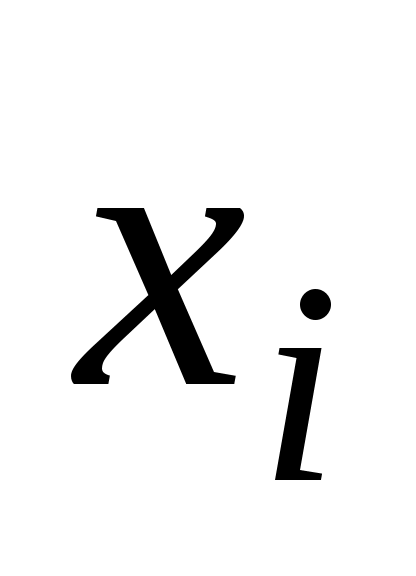
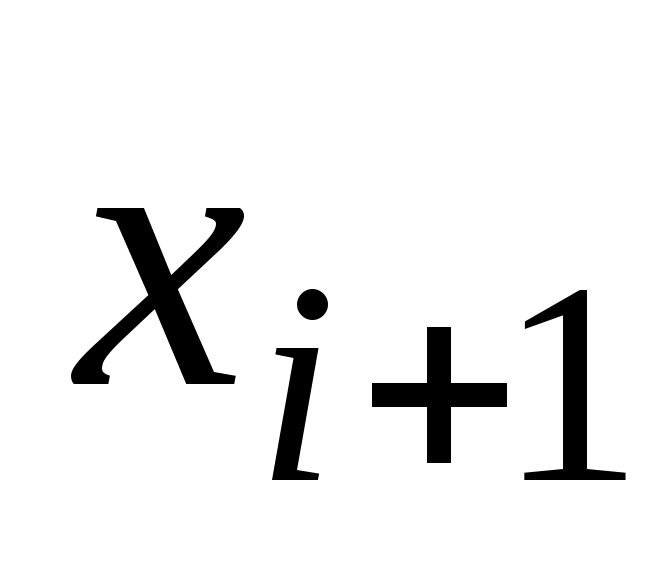
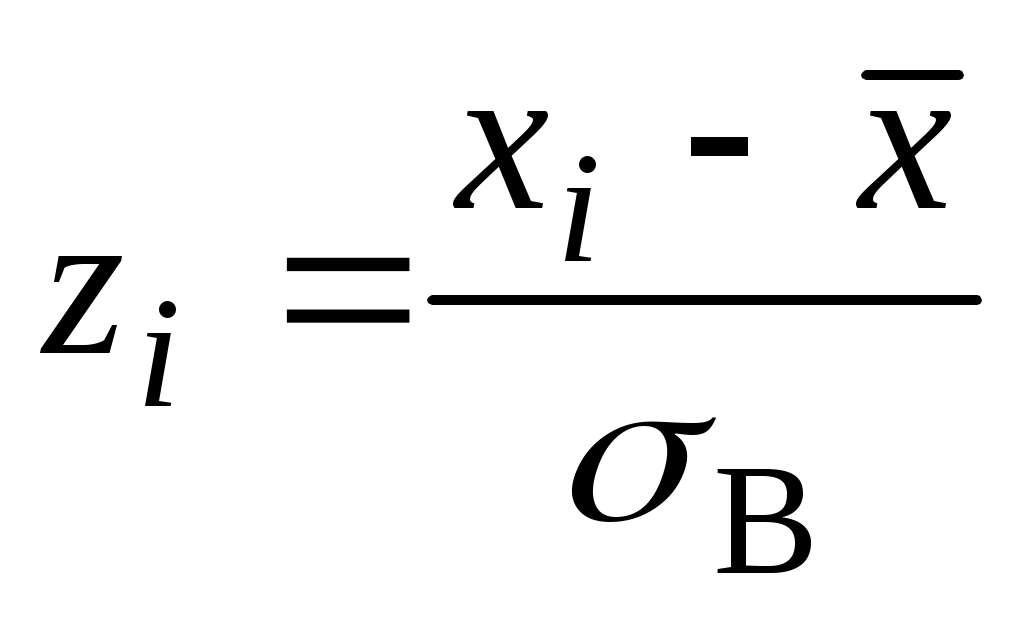
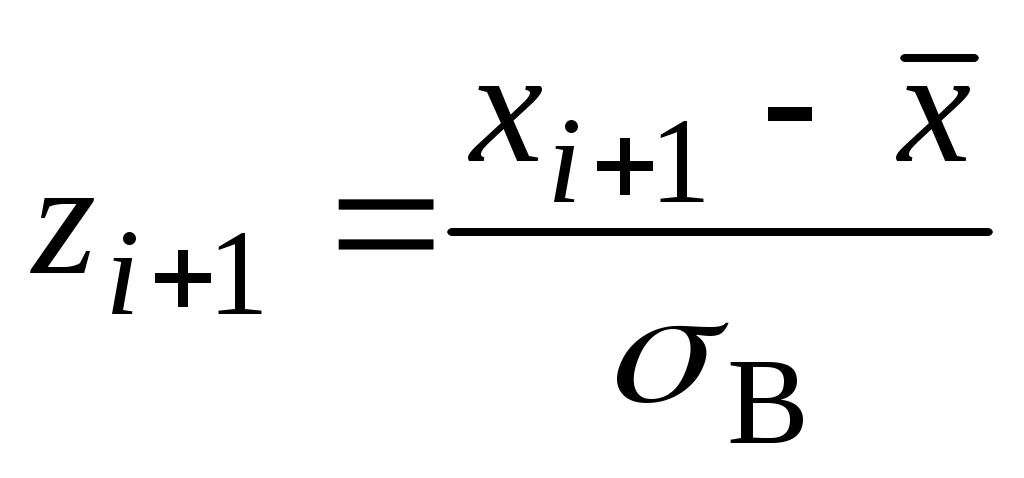
1
43,40 44,96
–
-0,49
-1,31
2
43,96 44,52
-0,49
-0,93
-1,31
-1,02
3
44,52 45,08
-0,93
-0,37
-1,02
-0,41
4
45,08 45,64
-0,37
0,19
-0,41
0,21
5
45,64 46,20
0,19
0,75
0,21
0,82
6
46,20 46,76
0,75
1,31
0,82
1,44
7
46,76 47,88
1,31
–
1,44
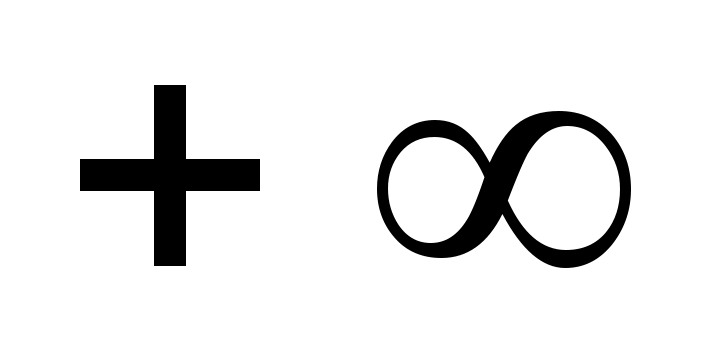
Находим теоретические вероятности
и теоретические частоты: 
. Составляем расчетную таблицу (табл. 4). Значения функции 
берём из прил.1.Таблица 4.
-
Границы интервала
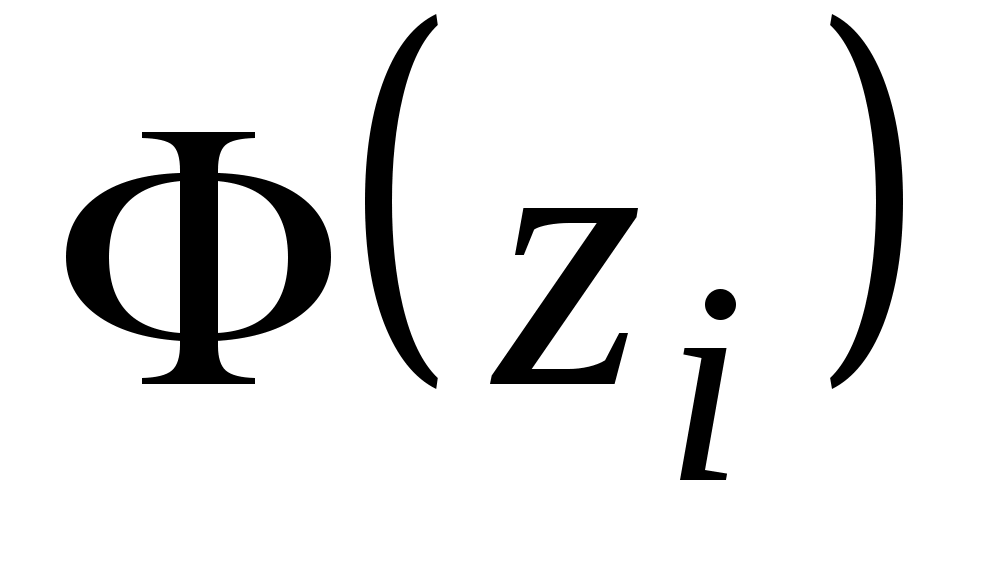
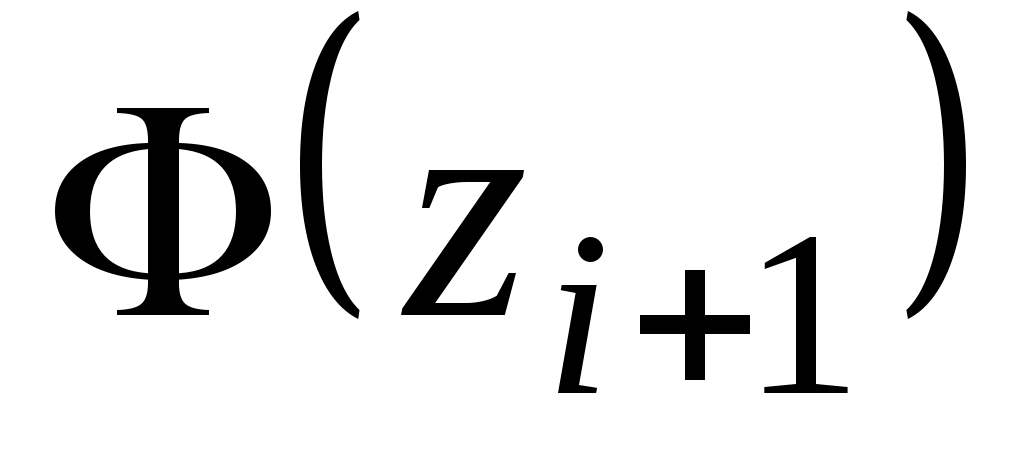
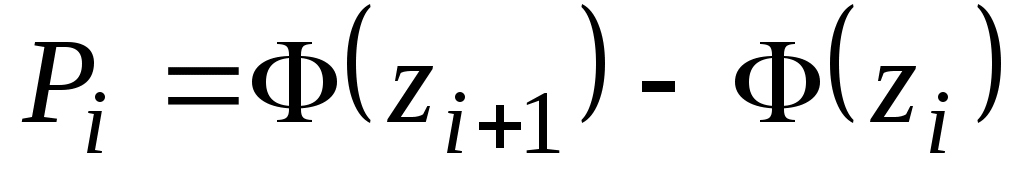
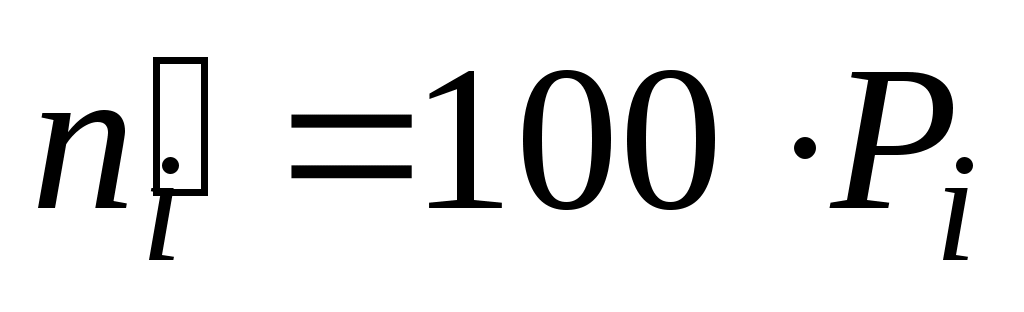
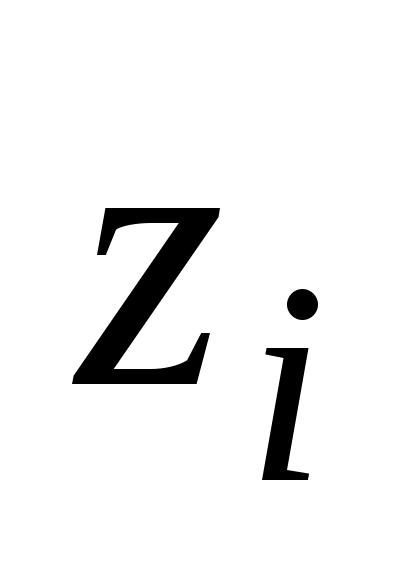
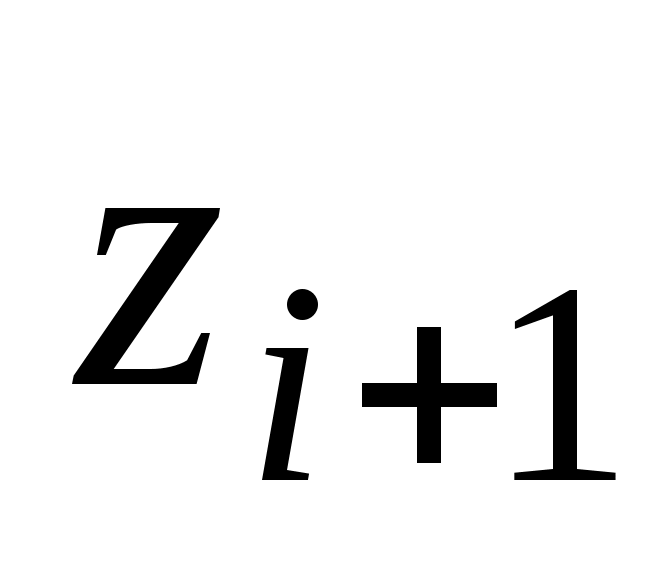
1
-1,31
-0,5000
-0,4049
0,0951
9,51
2
-1,31
-1,02
-0,4049
-0,3461
0,0588
5,88
3
-1,02
-0,41
-0,3461
-0,1591
0,1870
18,70
4
-0,41
0,21
-0,1591
0,0832
0,2423
24,23
5
0,21
0,82
0,0832
0,2939
0,2107
21,07
6
0,82
1,44
0,2939
0,4251
0,1312
13,12
7
1,44
0,4251
0,5000
0,0749
7,49
–
–
–
–
1
100
Вычислим наблюдаемое значение критерия Пирсона. Для этого составим расчетную таблицу (табл. 5). Последние два столбца служат для контроля вычислений по формуле:
Таблица 5
-
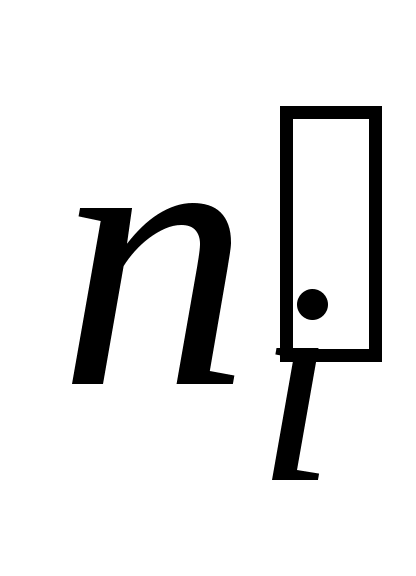
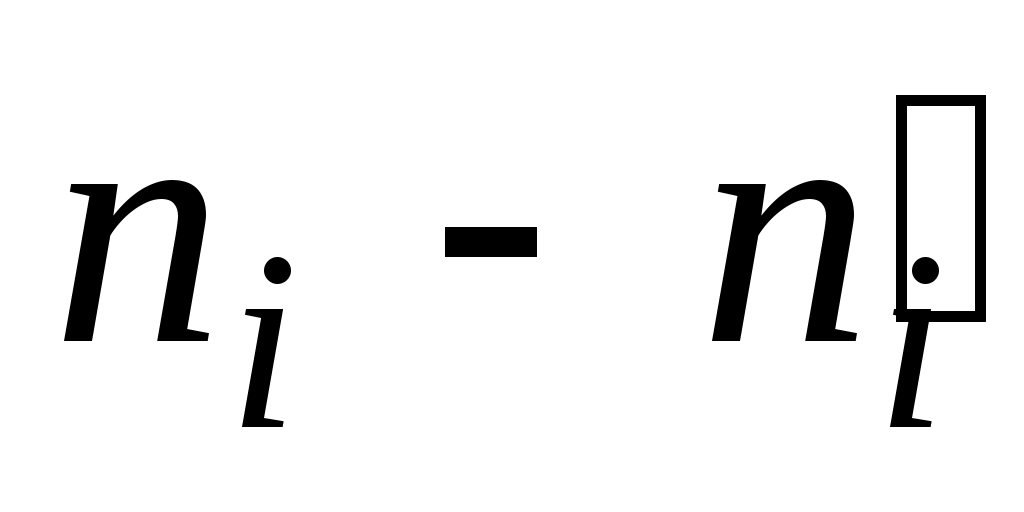
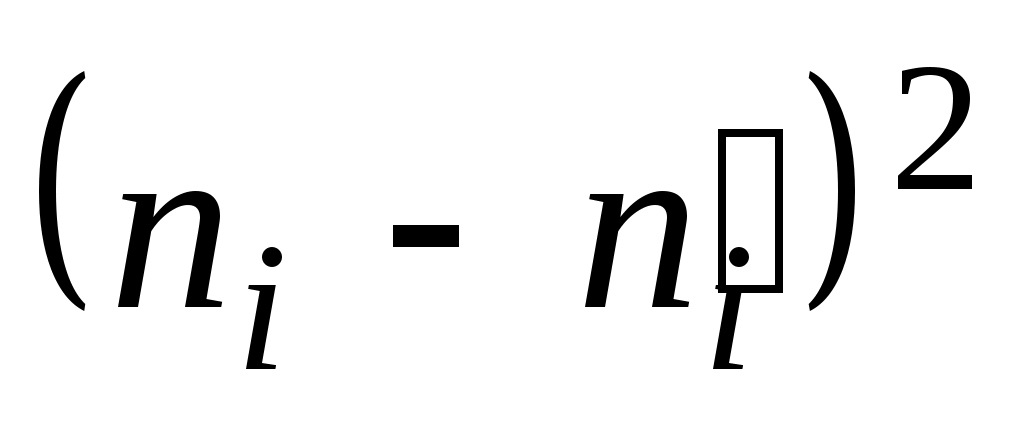
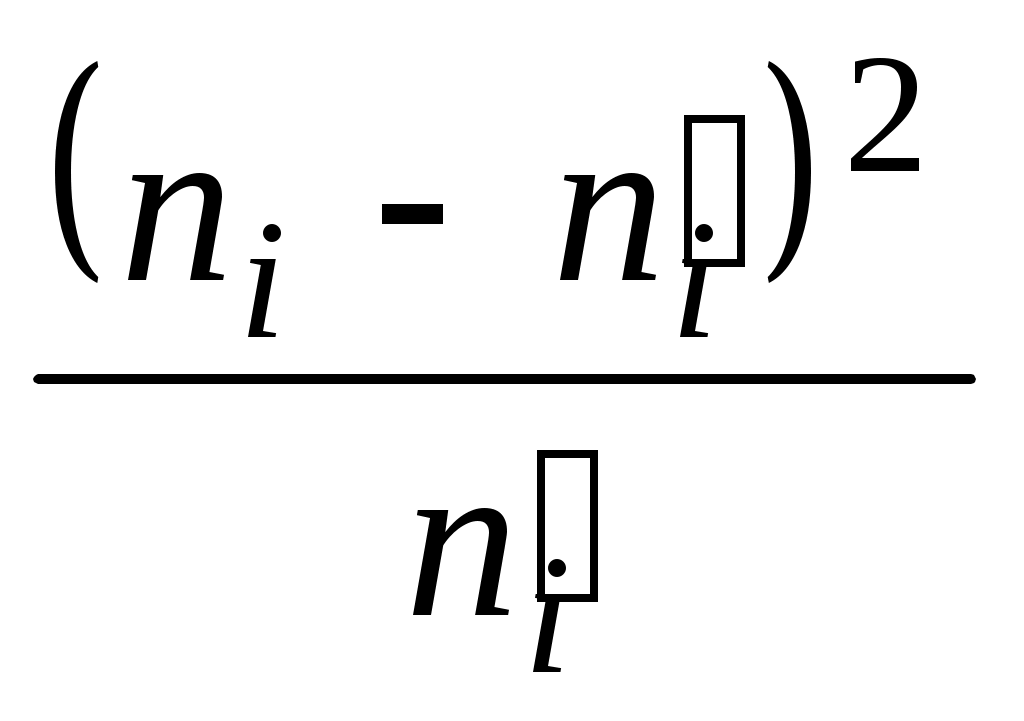
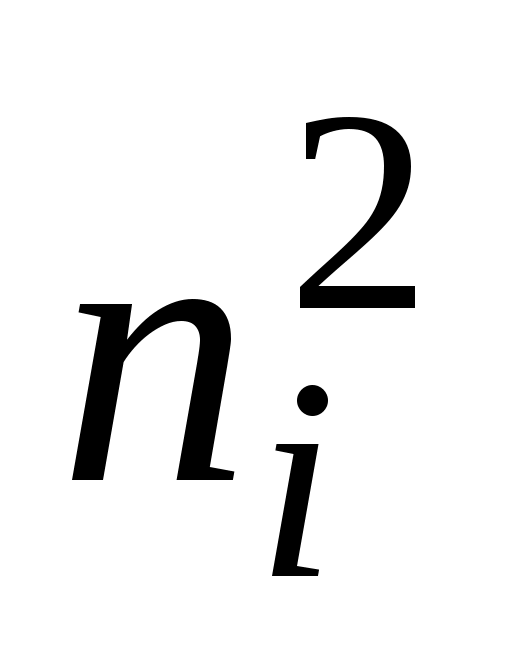
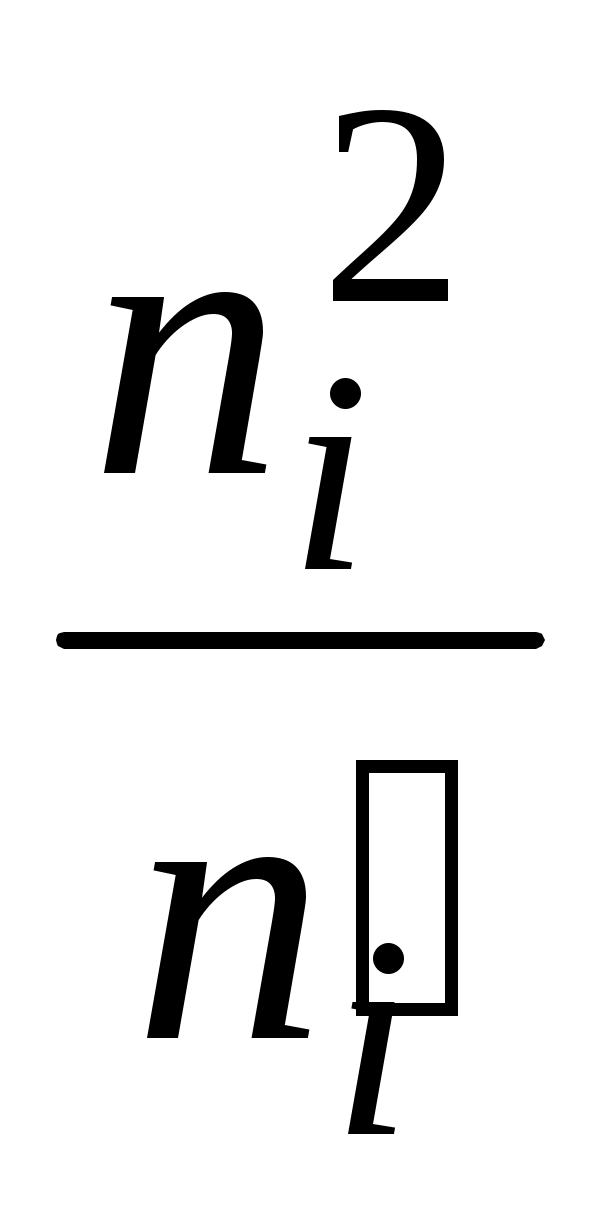
1
7
9,51
-2,51
6,3001
0,6625
49
5,1525
2
13
5,88
7,12
50,6944
8,6215
169
28,7415
3
12
18,70
-6,70
44,89
2,4005
144
7,7005
4
22
24,23
-2,23
4,9729
0,2052
484
19,9752
5
25
21,07
3,93
15,4449
0,7330
625
29,6630
6
14
13,12
0,88
0,7744
0,0590
196
14,9390
7
7
7,49
-0,49
0,2401
0,0321
49
6,5421
100
100
–
–
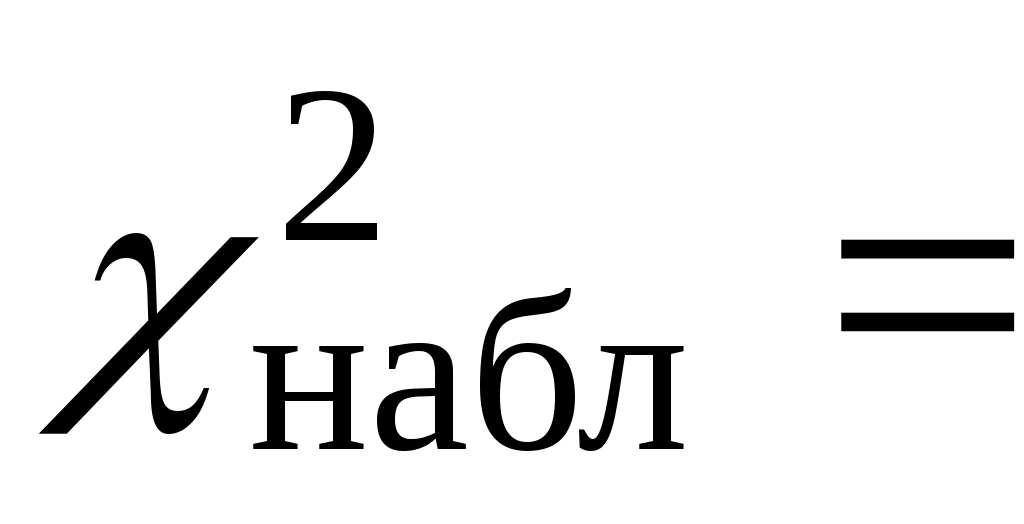12,7138
–
112,7138